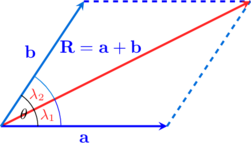
Besar Resultan
$|\textbf{R}| = \sqrt{|\textbf {a}|^2 + |\textbf {b}|^2 + 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}$
Arah Resultan
$\dfrac{|\textbf{R}|}{\sin \theta} = \dfrac{|\textbf{a}|}{\sin \lambda_2} = \dfrac{|\textbf{b}|}{\sin \lambda_1}$
CONTOH SOAL
Soal 1
Dua buah vektor gaya \(\textbf{F}_1 = 10 \text{ N}\) dan \(\textbf{F}_1 = 20 \text{ N}\) membentuk sudut \(60^{\circ}\).
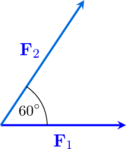
Tentukan:
(A) Besar resultan vektor
(B) Arah resultan yang diukur dari vektor \(\textbf{F}_1\)
(A) Menghitung besar resultan vektor
\begin{equation*}
\begin{split}
|\textbf{R}| &= \sqrt{|{\textbf{F}_1}|^2 + |{\textbf{F}_2}|^2 + 2\cdot |{\textbf{F}_1}|\cdot |{\textbf{F}_2}|\cdot \cos \theta}\\\\
|\textbf{R}| &= \sqrt{10^2 + 20^2 + 2\cdot 10\cdot 20\cdot \cos 60^{\circ}}\\\\
|\textbf{R}| &= \sqrt{100 + 400 + \cancel{2}\cdot 10\cdot 20\cdot \frac{1}{\cancel{2}}}\\\\
|\textbf{R}| &= \sqrt{500 + 200}\\\\
|\textbf{R}| &= \sqrt{700}\\\\
|\textbf{R}| &= 10\sqrt{7}\text{ N}\\\\
\end{split}
\end{equation*}
(B) Menghitung arah resultan yang diukur dari vektor \(\textbf{F}_1\)
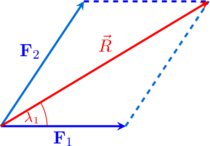
\begin{equation*}
\begin{split}
\dfrac{|\textbf{R}|}{\sin \theta} &= \dfrac{|{\textbf{F}_2}|}{\sin \lambda_1}\\\\
\dfrac{10\sqrt{7}}{\sin 60^{\circ}} &= \dfrac{20}{\sin \lambda_1}\\\\
\dfrac{\cancel{10}\sqrt{7}}{\frac{1}{2}\sqrt{3}} &= \dfrac{\cancelto{2}{20}}{\sin \lambda_1}\\\\
\dfrac{2\sqrt{7}}{\sqrt{3}} &= \dfrac{2}{\sin \lambda_1}\:\:\:\:\:\color{blue}\text{kali silang}\\\\
\cancel{2}\sqrt{7}\times \sin \lambda_1 &= \cancel{2}\times \sqrt{3}\\\\
\sin \lambda_1 &= \dfrac{\sqrt{3}}{\sqrt{7}}\times \color{blue}\dfrac{\sqrt{7}}{\sqrt{7}}\\\\
\sin \lambda_1 &= \dfrac{\sqrt{21}}{7}\\\\
\lambda_1 &= \sin^{-1}\dfrac{\sqrt{21}}{7}\\\\
\end{split}
\end{equation*}
Soal 2
Dua buah vektor besarnya sama mengapit sudut \(\theta\). Jika resultan kedua vektor sama dengan 4 kali selisihnya, maka tentukan nilai \(\cos \theta\)
Rumus resultan dua buah vektor:
$\color{blue}\text{Besar resultan}= \sqrt{|{\textbf{F}_1}|^2 + |{\textbf{F}_2}|^2 + 2\cdot |{\textbf{F}_1}|\cdot |{\textbf{F}_2}|\cdot \cos \theta}$
Rumus selisih dua buah vektor:
$\color{blue}\text{Besar selisih}= \sqrt{|{\textbf{F}_1}|^2 + |{\textbf{F}_2}|^2\:-\:2\cdot |{\textbf{F}_1}|\cdot |{\textbf{F}_2}|\cdot \cos \theta}$
Resultan kedua vektor sama dengan 4 kali selisihnya
\begin{equation*}
\begin{split}
\sqrt{|{\textbf{F}}|^2 + |{\textbf{F}}|^2 + 2\cdot |{\textbf{F}}|\cdot |{\textbf{F}}|\cdot \cos \theta}& = 4\sqrt{|{\textbf{F}}|^2 + |{\textbf{F}}|^2 \:-\: 2\cdot |{\textbf{F}}|\cdot |{\textbf{F}}|\cdot \cos \theta}\\\\
\sqrt{2|{\textbf{F}}|^2 + 2 |{\textbf{F}}|^2\cdot \cos \theta}& = 4\sqrt{2|{\textbf{F}}|^2\:-\:2 |{\textbf{F}}|^2\cdot \cos \theta}\:\:\:\:\:\color{blue}\text{kuadratkan kedua ruas}\\\\
2|{\textbf{F}}|^2 + 2 |{\textbf{F}}|^2\cdot \cos \theta& = 16(2|{\textbf{F}}|^2\:-\:2 |{\textbf{F}}|^2\cdot \cos \theta)\\\\
2|{\textbf{F}}|^2 + 2 |{\textbf{F}}|^2\cdot \cos \theta& = 32|{\textbf{F}}|^2\:-\:32 |{\textbf{F}}|^2\cdot \cos \theta\\\\
\cancel{|{\textbf{F}}|^2} (2 + 2\cos \theta)& = \cancel{|{\textbf{F}}|^2}(32 \:-\: 32 \cos \theta)\\\\
34\cos \theta& = 30\\\\
\cos \theta& = \dfrac{30}{34}\\\\
\cos \theta& = \dfrac{15}{17}\\\\
\end{split}
\end{equation*}
