Soal 1
Yang termasuk kelompok besaran vektor adalah …
(A) panjang, waktu, suhu
(B) kuat arus listrik, energi, daya
(C) jarak, kelajuan, massa
(D) percepatan, gaya, perpindahan
(E) usaha, energi, waktu
Jawaban: D
Besaran vektor adalah besaran yang memiliki nilai dan juga arah
Contoh besaran vektor: perpindahan, kecepatan, percepatan, gaya
Soal 2
Perhatikan diagram vektor di bawah ini:
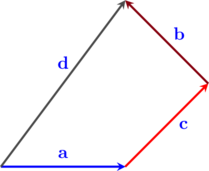
Penulisan diagram vektor di atas adalah …
(A) \(\textbf {a} + \textbf {d} + \textbf {b} = \textbf{c}\)
(B) \(\textbf {d} + \textbf {c} + \textbf {b} = \textbf {a}\)
(C) \(\textbf {a} + \textbf {c} + \textbf {b} = \textbf {d}\)
(D) \(\textbf {a} + \textbf {b} + \textbf {d} = \textbf {a}\)
(E) \(\textbf {b} + \textbf {d} +\textbf {a} = \textbf {c}\)
Jawaban: C
Soal 3
Dua buah gaya masing-masing 10 N dan 15 N membentuk sudut \(60^{\circ}\). Besar resultan kedua gaya tersebut adalah …
(A) \(5\sqrt{2} \text{ N}\)
(B) \(5\sqrt{3} \text{ N}\)
(C) \(5\sqrt{17} \text{ N}\)
(D) \(5\sqrt{19} \text{ N}\)
(E) \(5\sqrt{21} \text{ N}\)
Jawaban: D
\(|\textbf{R}| = \sqrt{|\textbf {a}|^2 + |\textbf {b}|^2 + 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}\)
\(|\textbf{R}| = \sqrt{10^2 + 15^2 + 2\cdot 10\cdot 15\cdot \cos 60^{\circ}}\)
\(|\textbf{R}| = \sqrt{100 + 225 + \cancel{2}\cdot 150\cdot \dfrac{1}{\cancel{2}}}\)
\(|\textbf{R}| = \sqrt{325 + 150}\)
\(|\textbf{R}| = \sqrt{475}\)
\(|\textbf{R}| = \sqrt{25\times 19}\)
\(|\textbf{R}| = 5\sqrt{19}\text{ N}\)
Soal 4
Dua buah vektor gaya masing-masing besarnya 7 N dan 24 N. Jika besar resultan kedua gaya tersebut adalah 25 N, maka besar sudut yang diapit oleh kedua vektor tersebut adalah …
(A) \(30^{\circ}\)
(B) \(60^{\circ}\)
(C) \(90^{\circ}\)
(D) \(120^{\circ}\)
(E) \(150^{\circ}\)
Jawaban: C
\(|\textbf{R}| = \sqrt{|\textbf {a}|^2 + |\textbf {b}|^2 + 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}\)
\(25 = \sqrt{7^2 + 24^2 + 2\cdot 7\cdot 24\cdot \cos \theta}\)
\(\color{blue}\text{kuadratkan kedua ruas}\)
\(625 = 49 + 576 + 336\cdot \cos \theta\)
\(625 = 625 + 336\cdot \cos \theta\)
\(625\:-\: 625 = 336\cdot \cos \theta\)
\(0 = 336\cdot \cos \theta\)
\(\cos \theta = 0\)
\(\theta = 90^{\circ}\)
Soal 5
Dua buah vektor gaya dengan besar yang sama yaitu 20 N membentuk sudut \(120^{\circ}\) satu sama lain. Besar selisih kedua vektor tersebut adalah …
(A) \(10 \text{ N}\)
(B) \(40 \text{ N}\)
(C) \(10\sqrt{3} \text{ N}\)
(D) \(20\sqrt{3} \text{ N}\)
(E) \(30\sqrt{3} \text{ N}\)
Jawaban: D
Besar selisih dua buah vektor:
\(sqrt{|\textbf {a}|^2 + |\textbf{b}|^2 \:-\: 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}\)
\(\sqrt{20^2 + 20^2 \:-\: 2\cdot 20\cdot 20\cdot \cos 120^{\circ}}\)
\(\sqrt{400 + 400 \:-\: \cancel{2}\cdot 400\cdot (-\dfrac{1}{\cancel{2}})}\)
\(\sqrt{800 + 400}\)
\(\sqrt{1200} = \sqrt{400 \times 3} = 20\sqrt{3} \text{ N}\)
Soal 6
Dua buah vektor \(\textbf {a}\) dan \(\textbf {b}\), besar vektor \(\textbf {a}\) sama dengan 2 kali besar vektor \(\textbf {b}\). Jika \(\dfrac{|\textbf {a}\:-\: \textbf {b}|}{|\textbf {a}+ \textbf {b}|} = \dfrac{1}{\sqrt{3}}\) maka nilai kosinus sudut apit kedua vektor tersebut adalah …
(A) \(\dfrac{1}{2}\)
(B) \(\dfrac{1}{3}\)
(C) \(\dfrac{3}{5}\)
(D) \(\dfrac{3}{8}\)
(E) \(\dfrac{5}{8}\)
Jawaban: E
\(\dfrac{\sqrt{|\textbf {a}|^2 + |\textbf{b}|^2 \:-\: 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}}{\sqrt{|\textbf {a}|^2 + |\textbf {b}|^2 + 2\cdot |\textbf {a}|\cdot |\textbf {b}|\cdot \cos \theta}} = \dfrac{1}{\sqrt{3}}\)
\(\dfrac{\sqrt{|\textbf {2b}|^2 + |\textbf {b}|^2 \:-\: 2\cdot |\textbf {2b}|\cdot |\textbf {b}|\cdot \cos \theta}}{\sqrt{|\textbf {2b}|^2 + |\textbf {b}|^2 + 2\cdot |\textbf {2b}|\cdot |\textbf {b}|\cdot \cos \theta}} = \dfrac{1}{\sqrt{3}}\)
\(\dfrac{\sqrt{4|\textbf {b}|^2 + |\textbf {b}|^2 \:-\: 2\cdot 2|\textbf {b}|^2\cdot \cos \theta}}{\sqrt{4|\textbf {b}|^2 + |\textbf {b}|^2 + 2\cdot 2|\textbf {b}|^2\cdot \cos \theta}} = \dfrac{1}{\sqrt{3}}\)
\(\color{blue}\text{kuadratkan kedua ruas}\)
\(\dfrac{4|\textbf {b}|^2 + |\textbf {b}|^2 \:-\: 2\cdot 2|\textbf {b}|^2\cdot \cos \theta}{4|\textbf {b}|^2 + |\textbf {b}|^2 + 2\cdot 2|\textbf {b}|^2\cdot \cos \theta} = \dfrac{1}{3}\)
\(\dfrac{5|\textbf {b}|^2 \:-\: 4|\textbf {b}|^2\cdot \cos \theta}{5|\textbf {b}|^2 + 4|\textbf {b}|^2\cdot \cos \theta} = \dfrac{1}{3}\)
\(\dfrac{\cancel{|\textbf {b}|^2}(5 \:-\: 4\cos \theta)}{\cancel{|\textbf {b}|^2}(5 + 4\cos \theta)} = \dfrac{1}{3}\)
\(\dfrac{5 \:-\: 4\cos \theta}{5 + 4\cos \theta} = \dfrac{1}{3}\)
\(\color{blue}\text{kali silang}\)
\(15 \:-\: 12\cdot \cos \theta = 5 + 4\cos \theta\)
\(15\:-\: 5 = 4\cos \theta + 12\cdot \cos \theta\)
\(10 = 16\cdot \cos \theta\)
\(\cos \theta = \dfrac{10}{16} = \dfrac{5}{8}\)
Soal 7
Sebuah mobil bergerak dengan kecepatan 60 km/jam membentuk sudut \(37^{\circ}\) terhadap sumbu x positif. Besar komponen vektor kecepatan tersebut pada sumbu x dan sumbu y berturut−turut adalah …
(A) 48 km/jam dan 36 km/jam
(B) 36 km/jam dan 48 km/jam
(C) 38 km/jam dan 42 km/jam
(D) 45 km/jam dan 48 km/jam
(E) 49 km/jam dan 50 km/jam
Jawaban: A
Besar komponen vektor kecepatan pada sumbu x:
\(|{\textbf{V}_{\textbf{x}}}| = |{\textbf{V}}|\cdot \cos 37^{\circ}\)
\(|{\textbf{V}_{\textbf{x}}}| = 60\cdot 0,8 = 48 \text{ km/jam}\)
Besar komponen vektor kecepatan pada sumbu y:
\(|{\textbf{V}_{\textbf{y}}}| = |{\textbf{V}}|\cdot \sin 37^{\circ}\)
\(|{\textbf{V}_{\textbf{y}}}| = 60\cdot 0,6 = 36 \text{ km/jam}\)
Soal 8
Sebuah vektor memiliki komponen dalam arah sumbu x dan sumbu y berturut−turut adalah \(-10\sqrt{3}\text{ N}\) dan \(-10 \text{ N}\). Besar dan arah vektor tersebut terhadap sumbu x positif adalah …
(A) \(10 \text{ N}; \: 30^{\circ}\)
(B) \(20 \text{ N}; \: 60^{\circ}\)
(C) \(20 \text{ N}; \: 210^{\circ}\)
(D) \(40 \text{ N}; \: 240^{\circ}\)
(E) \(60 \text{ N}; \: 280^{\circ}\)
Jawaban: C
\(\dfrac{|{\textbf{F}_{\textbf{y}}}|}{|{\textbf{F}_{\textbf{x}}}|} = \dfrac{-10\text{ N}}{-10\sqrt{3}\text{ N}}\)
\(\dfrac{|{\textbf{F}}|\cdot \sin \theta}{|{\textbf{F}}|\cdot \cos \theta} = \dfrac{\cancel{-10}\text{ N}}{\cancel{-10}\sqrt{3}\text{ N}}\)
\(\dfrac{\cancel{|{\textbf{F}}|}\cdot \sin \theta}{\cancel{|{\textbf{F}}|}\cdot \cos \theta} = \dfrac{1}{\sqrt{3}}\)
\(\tan \theta = \dfrac{1}{\sqrt{3}} = \dfrac{1}{3}\sqrt{3}\)
Karena komponen x negatif dan komponen y negatif maka vektor gaya berada pada kuadran III, dengan arah sebesar \(180^{\circ} + 30^{\circ} = 210^{\circ}\) diukur dari sumbu x positif berlawanan arah jarum jam
\(|{\textbf{F}}|\cdot \sin \theta = -10\text{ N}\)
\(|{\textbf{F}}|\cdot \sin 210^{\circ} = -10\text{ N}\)
\(|{\textbf{F}}|\cdot \left(-\dfrac{1}{2}\right) = -10\text{ N}\)
\(|{\textbf{F}}|= -10 \times \left(-\dfrac{2}{1}\right)\text{ N}\)
\(|{\textbf{F}}|= 20 \text{ N}\)
Soal 9
Seseorang melakukan perjalanan menggunakan mobil berangkat dari kota A ke kota B sejauh 8 km arah utara, dilanjutkan ke kota C arah timur 5 km dan akhirnya sampai di kota D sejauh 20 km arah selatan. Perpindahan mobil dari A sampai D adalah …
(A) 13 km
(B) 14 km
(C) 15 km
(D) 16 km
(E) 20 km
Jawaban: A
Sketsa perjalanan:
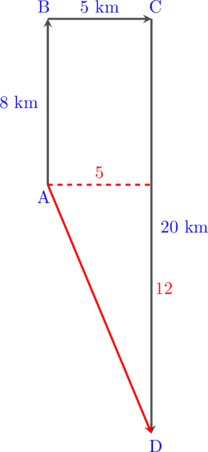
Dengan menggunakan rumus pythagoras,
\(\text{AD} = \sqrt{5^2 + 12^2}\)
\(\text{AD} = \sqrt{25 + 144}\)
\(\text{AD} = \sqrt{169} = 13\text{ km}\)
Soal 10
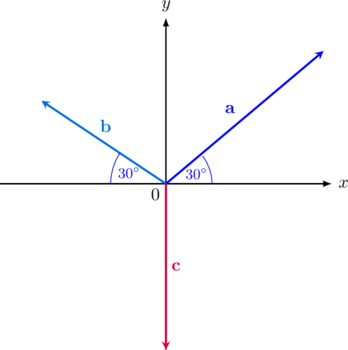
Jika \(|\textbf {a}| = 20 \text{ N}, |\textbf {b}| = 10 \text{ N}, \text{ dan } |\textbf {c}| = 30 \text{ N}\) maka besar dan arah resultan ketiga vektor tersebut adalah …
(A) \(\text{10 N}, 60^{\circ}\)
(B) \(10\sqrt{3}\text{ N}, 60^{\circ}\)
(C) \(10\sqrt{3}\text{ N}, 300^{\circ}\)
(D) \(20\sqrt{2}\text{ N}, 310^{\circ}\)
(E) \(20\sqrt{2}\text{ N}, 320^{\circ}\)
Jawaban: C
| Vektor | Komponen di Sumbu X (Rx) | Komponen di Sumbu Y (Ry) |
| $\textbf {a}$ | \(|\textbf{a}_x| = |\textbf{a}|\cdot \cos 30^{\circ}\)
\(|\textbf{a}_x| = 20\cdot \dfrac{1}{2}\sqrt{3} = 10\sqrt{3}\text{ N}\) |
\(|\textbf{a}_y| = |\textbf{a}|\cdot \sin 30^{\circ}\)
\(|\textbf{a}_y| = 20\cdot \dfrac{1}{2} = 10\text{ N}\) |
| $\textbf {b}$ | \(|\textbf{b}_x| = -|\textbf{b}|\cdot \cos 30^{\circ}\)
\(|\textbf{a}_x| = -10\cdot \dfrac{1}{2}\sqrt{3} = -5\sqrt{3}\text{ N}\) |
\(|\textbf{b}_y| = |\textbf{b}|\cdot \sin 30^{\circ}\)
\(|\textbf{a}_x| = 10\cdot \dfrac{1}{2} = 5\text{ N}\) |
| $\textbf {c}$ | \(0\text{ N}\) | \(-30 \text{ N}\) |
| Total | \(5\sqrt{3} \text{ N}\) | \(-15 \text{ N}\) |
\begin{equation*}
\begin{split}
|\textbf{R}| &= \sqrt{(|\textbf {R}_x|)^2 + (|\textbf {R}_y|)^2}\\\\
|\textbf{R}| &= \sqrt{(5\sqrt{3} )^2 + (-15)^2}\\\\
|\textbf{R}| &= \sqrt{75 + 225}\\\\
|\textbf{R}| &= \sqrt{300} = 10\sqrt{3}\text{ N}
\end{split}
\end{equation*}
Jadi, besar resultan vektornya adalah \(10\sqrt{3}\text{ N}\)
Vektor resultannya terletak di kuadran IV karena nilai Rx positif dan Ry negatif
\begin{equation*}
\begin{split}
\tan \alpha &= \dfrac{|\textbf {R}_y|}{|\textbf {R}_x|}\\\\
\tan \alpha &= \dfrac{-15}{5\sqrt{3}} = \dfrac{-3}{\sqrt{3}} = -\sqrt{3}\\\\
\alpha& = \tan^{-1} (-\sqrt{3}) = 300^{\circ}\:\:\:\:\:\color{blue}\text{sudut di kuadran IV}
\end{split}
\end{equation*}
Vektor resultannya memiliki arah \(300^{\circ}\) diukur dari sumbu x positif berlawanan arah dengan jarum jam
Soal 11
Diketahui empat buah vektor dengan besar dan arah sebagai berikut:
\(|{\textbf{F}_1}| = 10 \text{ N}, \text{ arah } 53^{\circ}\text{ terhadap sumbu x positif}\)
\(|{\textbf{F}_2}| = 5 \text{ N}, \text{ arah } -37^{\circ}\text{ terhadap sumbu x negatif}\)
\(|{\textbf{F}_3}| = 5 \text{ N}, \text{ arah } 37^{\circ}\text{ terhadap sumbu x negatif}\)
\(|{\textbf{F}_4}| = 20 \text{ N}, \text{ di sumbu y negatif}\)
Besar dan arah dari \({\textbf{F}_5 }= 2{\textbf{F}_1} + {\textbf{F}_2} + {\textbf{F}_3} + {\textbf{F}_4}\) adalah …
(A) \(3\sqrt{2}\text{ N}, 315^{\circ}\)
(B) \(4\sqrt{2}\text{ N}, 315^{\circ}\)
(C) \(4\sqrt{2}\text{ N}, 45^{\circ}\)
(D) \(6\sqrt{2}\text{ N}, 225^{\circ}\)
(E) \(6\sqrt{2}\text{ N}, 315^{\circ}\)
Jawaban: B
Gambar masing-masing vektor:
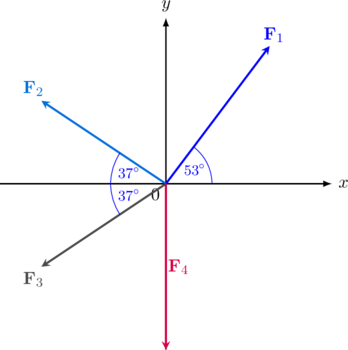
| Vektor | Komponen di Sumbu X (Rx) | Komponen di Sumbu Y (Ry) |
| $2{\textbf{F}_1}$ | \(|2{\textbf{F}_{1x}}| = |2{\textbf{F}_1}|\cdot \cos 53^{\circ}\)
\(|2{\textbf{F}_{1x}}| = 20\cdot 0,6 = 12\text{ N}\) |
\(|2{\textbf{F}_{1y}}| = |2{\textbf{F}_1}|\cdot \sin 53^{\circ}\)
\(|2{\textbf{F}_{1y}}| = 20\cdot 0,8 = 16\text{ N}\) |
| ${\textbf{F}_2}$ | \(|{\textbf{F}_{2x}}| = -|{\textbf{F}_2}|\cdot \cos 37^{\circ}\)
\(|{\textbf{F}_{2x}}| = -5\cdot 0,8 = -4\text{ N}\) |
\(|{\textbf{F}_{2y}}| = |{\textbf{F}_2}|\cdot \sin 37^{\circ}\)
\(|{\textbf{F}_{2y}}| = 5\cdot 0,6 = 3\text{ N}\) |
| ${\textbf{F}_3}$ | \(|{\textbf{F}_{3x}}| = -| {\textbf{F}_3}|\cdot \cos 37^{\circ}\)
\(|{\textbf{F}_{3x}}| = -5\cdot 0,8 = -4\text{ N}\) |
\(|{\textbf{F}_{3y}}| =- |{\textbf{F}_3}|\cdot \sin 37^{\circ}\)
\(|{\textbf{F}_{3y}}| = -5\cdot 0,6 = -3\text{ N}\) |
| ${\textbf{F}_4}$ | \(0\) | \(-\text{20 N}\) |
| Total | \(4 \text{ N}\) | \(-4 \text{ N}\) |
\begin{equation*}
\begin{split}
|\textbf{R}| &= \sqrt{(|\textbf {R}_x|)^2 + (|\textbf {R}_y|)^2}\\\\
|\textbf{R}| &= \sqrt{4^2 + (-4)^2}\\\\
|\textbf{R}| &= \sqrt{16 + 16}\\\\
|\textbf{R}| &= \sqrt{32} = 4\sqrt{2}\text{ N}
\end{split}
\end{equation*}
Jadi, besar resultan vektornya adalah \(4\sqrt{2}\text{ N}\)
Vektor resultannya terletak di kuadran IV karena nilai Rx positif dan Ry negatif
\begin{equation*}
\begin{split}
\tan \alpha &= \dfrac{|\textbf {R}_y|}{|\textbf {R}_x|}\\\\
\tan \alpha &= \dfrac{-4}{4} = -1\\\\
\alpha& = 360^{\circ}\:-\:45^{\circ} = 315^{\circ}
\end{split}
\end{equation*}
Sudut di kuadran IV
Vektor resultannya memiliki arah \(315^{\circ}\) diukur dari sumbu x positif berlawanan arah dengan jarum jam
