Contoh 1
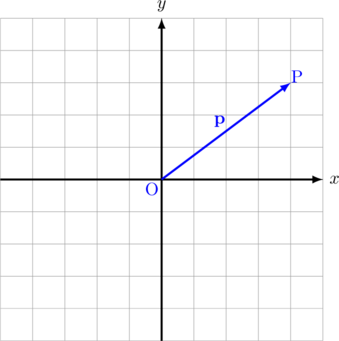
Cara menggambar vektor posisi \(\overrightarrow{\text{OP}}= \textbf{p} = \left(\begin{array}{c}4\\ 3\end{array}\right)\) atau dapat ditulis juga \(\textbf{p} = 4\textbf{i} + 3\textbf{j}\)
Tarik garis dari titik O, 4 satuan ke kanan, kemudian 3 satuan ke atas, sehingga terbentuk sinar garis yang berujung di titik P.
Contoh 2
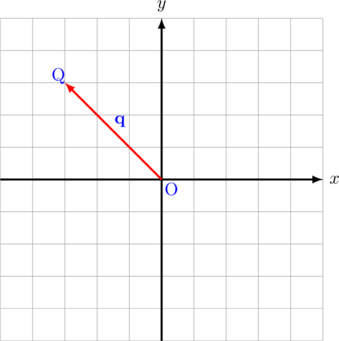
Cara menggambar vektor posisi \(\overrightarrow{\text{OQ}}= \textbf{q} = \left(\begin{array}{c}-3\\ 3\end{array}\right)\) atau dapat ditulis juga \(\textbf{q} = -3\textbf{i} + 3\textbf{j}\)
Tarik garis dari titik O, 3 satuan ke kiri, kemudian 3 satuan ke atas, sehingga terbentuk sinar garis yang berujung di titik Q.
Contoh 3
Cara menggambar vektor \(\overrightarrow{\text{PQ}}\), jika diketahui \(\textbf{p} = \left(\begin{array}{c}4\\ 3\end{array}\right)\) dan \(\textbf{q} = \left(\begin{array}{c}-3\\ 3\end{array}\right)\)
Tarik garis dari titik P sehingga terbentuk sinar garis yang berujung di titik Q.
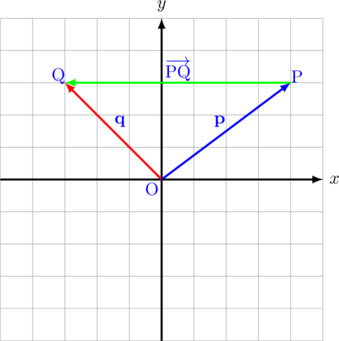
Dengan metode segitiga, hubungan antara ketiga vektor tersebut dapat ditulis:
\(\overrightarrow{\text{OP}} + \overrightarrow{\text{PQ}} = \overrightarrow{\text{OQ}}\)
\(\textbf{p} + \overrightarrow{\text{PQ}} = \textbf{q}\)
\(\overrightarrow{\text{PQ}} = \textbf{q}\:-\:\textbf{p}\)
\(\overrightarrow{\text{PQ}} = \left(\begin{array}{c}-3\\ 3\end{array}\right)\:-\:\left(\begin{array}{c}4\\ 3\end{array}\right)\)
\(\overrightarrow{\text{PQ}} = \left(\begin{array}{c}-3\:-\:4\\ 3\:-\:3\end{array}\right)\)
\(\overrightarrow{\text{PQ}} = \left(\begin{array}{c}-7\\ 0\end{array}\right)\)
