Dua buah vektor dikatakan sama apabila kedua vektor tersebut memiliki besar/panjang dan arah yang sama.
Contoh: \(\textbf{p} =\textbf{q}\)
\(\textbf{p}\) dan \(\textbf{q}\) adalah dua vektor yang sama, karena memiliki panjang dan arah yang sama.
Contoh Soal
Soal 1
Perhatikan gambar
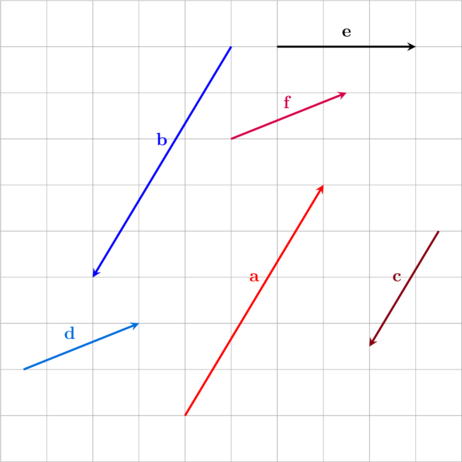
A. Tentukan pasangan vektor yang sama
B. Tentukan pasangan vektor yang memiliki panjang yang sama, tetapi arahnya berlawanan
Soal 2
Diketahui \(\textbf{m} = \left(\begin{array}{c}a + 3\\ 2b\end{array}\right)\) dan \(\textbf{n} = \left(\begin{array}{c}5\\ -4\end{array}\right)\). Jika \(\textbf{m} = \textbf{n}\), maka tentukan nilai \(a + b\).
Soal 3
Diketahui sebuah jajargenjang ABCD, memiliki koordinat titik A\((0, 0)\), B\((m, 0)\), C\((8, 3)\), dan D\((2, n)\). Tentukan nilai \(m + n\).
