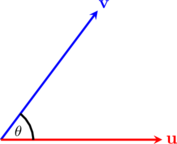
Sudut terkecil yang dibentuk oleh vektor \(\textbf{u}\) dan \(\textbf{v}\), dihitung sebagai berikut:
\(\cos \theta = \dfrac{\textbf{u} \cdot \textbf{v}}{||\textbf{u}|| \cdot ||\textbf{v}||}\)
\(\cos 90^{\circ} = \dfrac{\textbf{u} \cdot \textbf{v}}{||\textbf{u}|| \cdot ||\textbf{v}||}\)
\(\cos 0^{\circ} = \dfrac{\textbf{u} \cdot \textbf{v}}{||\textbf{u}|| \cdot ||\textbf{v}||}\)
\(\color{blue} \textbf{u} \cdot \textbf{v} = ||\textbf{u}|| \cdot ||\textbf{v}||\)
Tentukan besar sudut yang dibentuk oleh vektor \(\textbf{u}\) dan \(\textbf{v}\) di bawah ini:
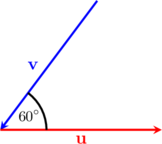
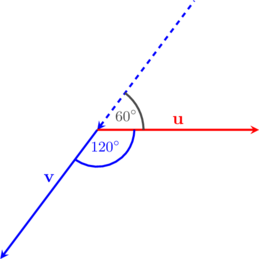
Sudut yang dibentuk antara vektor \(\textbf{u}\) dan \(\textbf{v}\) adalah \(180^{\circ}\:-\:60^{\circ} = 120^{\circ}\)
Diketahui vektor \(\textbf{a} = 2\textbf{i}\:-\:\textbf{j} + 2\textbf{k}\) dan vektor \(\textbf{b} = 3\textbf{j}\:-\:4\textbf{k}\). Tentukan cosinus sudut antara kedua vektor tersebut, dan tentukan jenis sudutnya.
\(\cos \theta = \dfrac{\textbf{a} \cdot \textbf{b}}{||\textbf{a}|| \cdot ||\textbf{b}||}\)
\(\cos \theta = \dfrac{\left(\begin{array}{c}2\\ -1\\2\end{array}\right) \cdot \left(\begin{array}{c}0\\ 3\\-4\end{array}\right)}{\sqrt{2^2 + (-1)^2 + 2^2}\cdot \sqrt{0^2 + 3^2 + (-4)^2}}\)
\(\cos \theta = \dfrac{0\:-\:3\:-\:8}{\sqrt{9}\cdot \sqrt{25}}\)
\(\cos \theta = \dfrac{-11}{3\cdot 5}\)
\(\cos \theta = \dfrac{-11}{15}\)
Karena hasil \(\cos \theta\) negatif, maka jenis sudut \(\theta\) adalah sudut tumpul.
Jika sudut yang dibentuk oleh vektor \(\textbf{u} = -2\textbf{i} + 6\textbf{j}\) dan \(\textbf{v} = m\textbf{i} + 3\textbf{j}\) adalah \(90^{\circ}\), maka tentukan nilai \(m\) yang memenuhi.
Vektor \(\textbf{u}\) dan \(\textbf{v}\) saling tegak lurus (membentuk sudut 90°), maka berlaku \(\textbf{u}\cdot \textbf{v} = 0\)
\(\left(\begin{array}{c}-2\\ 6\end{array}\right) \cdot \left(\begin{array}{c}m\\ 3\end{array}\right) = 0\)
\(-2m + 6(3) = 0\)
\(-2m + 18 = 0\)
\(-2m = -18\)
\(m = \frac{-18}{-2} = 9\)
Tentukan nilai \(m\) yang memenuhi agar vektor \(\textbf{a} = (m + 2)\textbf{i} \:-\:\textbf{j} + 2\textbf{k}\) dan vektor \(\textbf{b} = \textbf{i} \:-\:m\textbf{j} + \textbf{k}\) saling tegak lurus.
Vektor \(\textbf{a}\) dan \(\textbf{b}\) saling tegak lurus, maka \(\textbf{a}\cdot \textbf{b} = 0\)
\(\left(\begin{array}{c}m + 2\\ -1\\2\end{array}\right) \cdot \left(\begin{array}{c}1\\ -m\\1\end{array}\right) = 0\)
\(m + 2 + m + 2 = 0\)
\(2m + 4 = 0\)
\(2m = -4\)
\(m = -2\)
Jika \(\theta\) adalah sudut antara vektor \(\textbf{a}\) dan \(\textbf{b}\) dan hasil dari \(\textbf{a}\cdot \textbf{b} = -\dfrac{1}{2}\sqrt{2}||\textbf{a}||\cdot ||\textbf{b}||\), maka tentukan nilai \(\theta\).
\(\cos \theta = \dfrac{\textbf{a} \cdot \textbf{b}}{|\textbf{a}| \cdot |\textbf{b}|}\)
\(\cos \theta = \dfrac{-\frac{1}{2}\sqrt{2}\cancel{||\textbf{a}||\cdot ||\textbf{b}||}}{\cancel{||\textbf{a}|| \cdot ||\textbf{b}||}}\)
\(\cos \theta = -\dfrac{1}{2}\sqrt{2}\)
\(\theta = 180^{\circ}\:-\:45^{\circ}\)
\(\theta = 135^{\circ}\)
Suatu segitiga ABC, memiliki koordinat titik A(0, 2, 3), B(1, 4, 4), dan C(1, 0 , 2). Tentukan besar cosinus sudut ABC.
Sudut ABC dibentuk oleh vektor \(\overrightarrow{\text{BC}}\) dan \(\overrightarrow{\text{BA}}\) (titik pangkal kedua vektor berada di titik B)
\(\overrightarrow{\text{BC}} = \textbf{c}\:-\:\textbf{b}\)
\(\overrightarrow{\text{BC}} = \left(\begin{array}{c}1\\ 0\\2\end{array}\right)\:-\:\left(\begin{array}{c}1\\ 4\\4\end{array}\right) =\left(\begin{array}{c}0\\ -4\\-2\end{array}\right) \)
\(\overrightarrow{\text{BA}} = \textbf{a}\:-\:\textbf{b}\)
\(\overrightarrow{\text{BA}} = \left(\begin{array}{c}0\\ 2\\3\end{array}\right)\:-\:\left(\begin{array}{c}1\\ 4\\4\end{array}\right) = \left(\begin{array}{c}-1\\ -2\\-1\end{array}\right)\)
\(\cos \theta = \dfrac{\overrightarrow{\text{BC}} \cdot \overrightarrow{\text{BA}}}{|\overrightarrow{\text{BC}}|\cdot |\overrightarrow{\text{BA}}|}\)
\(\cos \theta = \dfrac{\left(\begin{array}{c}0\\ -4\\-2\end{array}\right)\cdot \left(\begin{array}{c}-1\\ -2\\-1\end{array}\right)}{\sqrt{0^2 + (-4)^2 + (-2)^2} \cdot \sqrt{(-1)^2 + (-2)^2 + (-1)^2}}\)
\(\cos \theta = \dfrac{(0)(-1) + (-4)(-2) + (-2)(-1)}{\sqrt{20} \cdot \sqrt{6}}\)
\(\cos \theta = \dfrac{10}{\sqrt{120}}\)
\(\cos \theta = \dfrac{10}{2\sqrt{30}}\)
\(\cos \theta = \dfrac{5}{\sqrt{30}} \times \color{red}\dfrac{\sqrt{30}}{\sqrt{30}} \)
\(\cos \theta = \dfrac{5\sqrt{30}}{30}\)
\(\cos \theta = \frac{1}{6}\sqrt{30}\)
Jadi, besar cosinus sudut ABC adalah \(\frac{1}{6}\sqrt{30}\)
