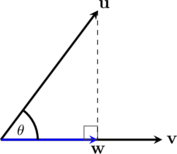
Proyeksi vektor ortogonal \(\textbf{u}\) pada \(\textbf{v}\) menghasilkan vektor \(\textbf{w}\)
\(\textbf{w} = \dfrac{\textbf{u} \cdot \textbf{v}}{(||\textbf{v}||)^2} \cdot \textbf{v}\)
Sedangkan panjang proyeksi vektor \(\textbf{u}\) pada \(\textbf{v}\) adalah \(||\textbf{w}||\)
Tentukan proyeksi vektor ortogonal \(\textbf{u} = -\textbf{i} + 2\textbf{j}\) pada \(\textbf{v} = 3\textbf{i} \:-\: \textbf{j}\).
Misal hasil vektor proyeksi \(\textbf{u}\) pada \(\textbf{v}\) adalah \(\textbf{w}\)
\(\textbf{w} = \dfrac{\textbf{u} \cdot \textbf{v}}{(||\textbf{v}||)^2} \cdot \textbf{v}\)
\(\textbf{w} = \dfrac{\left(\begin{array}{c}-1\\ 2\end{array}\right) \cdot \left(\begin{array}{c}3\\ -1\end{array}\right)}{(\sqrt{3^2 + (-1)^2})^2} \cdot \left(\begin{array}{c}3\\ -1\end{array}\right)\)
\(\textbf{w} = \dfrac{(-1)(3) + (2)(-1)}{3^2 + (-1)^2} \cdot \left(\begin{array}{c}3\\ -1\end{array}\right)\)
\(\textbf{w} = \dfrac{-5}{10} \cdot \left(\begin{array}{c}3\\ -1\end{array}\right)\)
\(\textbf{w} = -\dfrac{1}{2} \cdot \left(\begin{array}{c}3\\ -1\end{array}\right)\)
\(\textbf{w} = \left(\begin{array}{c}-\dfrac{3}{2}\\ \dfrac{1}{2}\end{array}\right)\)
\(\textbf{w} = -\dfrac{3}{2}\textbf{i}+ \dfrac{1}{2}\textbf{j} \)
Jadi hasil vektor proyeksi \(\textbf{u}\) pada \(\textbf{v}\) adalah \(\textbf{w} = -\frac{3}{2}\textbf{i} + \frac{1}{2}\textbf{j} \)
Tentukan proyeksi skalar vektor \(\textbf{v} = 4\textbf{i} + \textbf{j}\) pada \(\textbf{u} = -2\textbf{i} \:-\: 3\textbf{j}\).
Proyeksi skalar (panjang proyeksi) vektor \(\textbf{v}\) pada \(\textbf{u}\) adalah \(||\textbf{w}||\)
\(||\textbf{w}|| = \dfrac{|\textbf{v} \cdot \textbf{u}|}{||\textbf{u}||}\)
\(||\textbf{w}|| = \dfrac{\left|\left(\begin{array}{c}4\\ 1\end{array}\right) \cdot \left(\begin{array}{c}-2\\ -3\end{array}\right)\right|}{\sqrt{(-2)^2 + (-3)^2}}\)
\(||\textbf{w}|| = \dfrac{|(4)(-2) + (1)(-3)|}{\sqrt{4 + 9}}\)
\(||\textbf{w}|| = \dfrac{11}{\sqrt{13}}\times \color{red} \dfrac{\sqrt{13}}{\sqrt{13}}\)
\(||\textbf{w}|| = \dfrac{11}{13}\sqrt{13}\)
Jadi proyeksi skalar \(\textbf{v}\) pada \(\textbf{u}\) adalah \(||\textbf{w}|| = \dfrac{11}{13}\sqrt{13}\) satuan
