Perkalian silang antara vektor \(\textbf{a} = a_1\textbf{i} + a_2\textbf{j} + a_3\textbf{k}\) dengan \(\textbf{b} = b_1\textbf{i} + b_2\textbf{j} + b_3\textbf{k}\) dihitung sebagai berikut:
\(\textbf{a} \times \textbf{b} = \begin{vmatrix}\textbf{i}&\textbf{j}&\textbf{k}\\a_1 & a_2 & a_3\\b_1 & b_2 & b_3\end{vmatrix}\)
\(\textbf{a} \times \textbf{b} =\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix}\textbf{i}\:-\:\begin{vmatrix}a_1 & a_3\\ b_1 & b_3\end{vmatrix}\textbf{j} + \begin{vmatrix}a_1 & a_2\\ b_1 & b_2\end{vmatrix}\textbf{k}\)
\(\textbf{a} \times \textbf{b} =(a_2\cdot b_3\:-\:a_3\cdot b_2)\textbf{i}\:-\:(a_1\cdot b_3\:-\:a_3\cdot b_1)\textbf{j} + (a_1\cdot b_2\:-\:a_2\cdot b_1)\textbf{k}\)
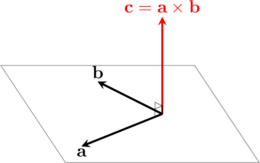
Hasil perkalian silang antara vektor \(\textbf{a}\) dengan vektor \(\textbf{b}\) akan menghasilkan suatu vektor \(\textbf{c}\) yang tegak lurus terhadap kedua vektor tersebut.
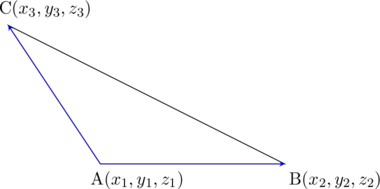
\(\color{blue} \text{Luas Segitiga } = \dfrac{1}{2} \left|\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}}\right|\)
\(\overrightarrow{\text{AB}}=\textbf{b}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AB}}=\left(\begin{array}{c}x_2\\ y_2\\z_2\end{array}\right) \:-\: \left(\begin{array}{c}x_1\\y_1\\z_1\end{array}\right)\)
\(\overrightarrow{\text{AC}}=\textbf{c}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AC}}=\left(\begin{array}{c}x_3\\ y_3\\z_3\end{array}\right) \:-\: \left(\begin{array}{c}x_1\\y_1\\z_1\end{array}\right)\)
Tentukan perkalian silang antara vektor \(\textbf{a} = -\textbf{i} + 2\textbf{j} + 3\textbf{k}\) dengan \(\textbf{b} = 4\textbf{i} \:-\:\textbf{j} + 5\textbf{k}\)
\(\textbf{a} \times \textbf{b} = \begin{vmatrix}\textbf{i}&\textbf{j}&\textbf{k}\\-1 & 2 & 3\\4 & -1 & 5\end{vmatrix}\)
\(\textbf{a} \times \textbf{b} =\begin{vmatrix}2 & 3\\ -1 & 5\end{vmatrix}\textbf{i}\:-\:\begin{vmatrix}-1 & 3\\ 4 & 5\end{vmatrix}\textbf{j} + \begin{vmatrix}-1 & 2\\ 4 & -1\end{vmatrix}\textbf{k}\)
\(\textbf{a} \times \textbf{b} =(2\cdot 5\:-\:3\cdot (-1))\textbf{i}\:-\:(-1\cdot 5\:-\:3\cdot 4)\textbf{j} + (-1\cdot (-1)\:-\:2\cdot 4)\textbf{k}\)
\(\textbf{a} \times \textbf{b} =13\textbf{i}\:-\:(-17)\textbf{j} + (-7)\textbf{k}\)
\(\textbf{a} \times \textbf{b} =13\textbf{i} + 17\textbf{j} \:-\:7\textbf{k}\)
Jadi, hasil perkalian silang antara vektor \(\textbf{a}\) dengan \(\textbf{b}\) adalah \(\textbf{c} = 13\textbf{i} + 17\textbf{j} \:-\:7\textbf{k}\)
Vektor \(\textbf{c}\) ini tegak lurus terhadap vektor \(\textbf{a}\) dan juga terhadap vektor \(\textbf{b}\)
\(\overrightarrow{\text{AB}}=\textbf{b}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AB}}=\left(\begin{array}{c}3\\ -2\\0\end{array}\right) \:-\: \left(\begin{array}{c}2\\0\\-1\end{array}\right) = \left(\begin{array}{c}1\\-2\\1\end{array}\right)\)
\(\overrightarrow{\text{AC}}=\textbf{c}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AC}}=\left(\begin{array}{c}4\\ 4\\1\end{array}\right) \:-\: \left(\begin{array}{c}2\\0\\-1\end{array}\right) = \left(\begin{array}{c}2\\4\\2\end{array}\right)\)
\(\color{blue} \text{Area of triangle } = \dfrac{1}{2} \left|\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}}\right|\)
\(\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}} = \left(\begin{array}{c}1\\-2\\1\end{array}\right)\times \left(\begin{array}{c}2\\4\\2\end{array}\right)\)
\(\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}} =\begin{vmatrix}\textbf{i}&\textbf{j}&\textbf{k}\\1 & -2 & 1\\2 & 4 & 2\end{vmatrix}\)
\(\overrightarrow{\text{AB}}\times \overrightarrow{\text{AC}} =\begin{vmatrix}-2 & 1\\ 4& 2\end{vmatrix}\textbf{i}\:-\:\begin{vmatrix}1&1\\ 2& 2\end{vmatrix}\textbf{j} + \begin{vmatrix}1 & -2\\ 2 & 4\end{vmatrix}\textbf{k}\)
\(\overrightarrow{\text{AB}}\times \overrightarrow{\text{AC}} =(-2\cdot 2\:-\:1\cdot 4)\textbf{i}\:-\:(1\cdot 2\:-\:1\cdot 2)\textbf{j} + (1\cdot 4\:-\:(-2)\cdot 2)\textbf{k}\)
\(\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}} =-8\textbf{i}\:-\:0\textbf{j} +8\textbf{k}\)
\(\overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}} = -8\textbf{i} + 8\textbf{k}\)
\(\text{Area of triangle } = \dfrac{1}{2}\sqrt{(-8)^2 + 8^2}\)
\(\text{Area of triangle } = \dfrac{1}{2}\sqrt{64 + 64}\)
\(\text{Area of triangle } = \dfrac{1}{2}\sqrt{2\times 64}\)
\(\text{Area of triangle } = \dfrac{8}{2}\sqrt{2}\)
\(\text{Area of triangle } = 4\sqrt{2} \text{ square units}\)
