Mengubah Koordinat Kartesius Menjadi Koordinat Polar
Titik \((x, y)\) dapat diubah menjadi koordinat polar \((r, \alpha)\)
\(r = \sqrt{x^2 + y^2}\)
\(\tan \alpha = \dfrac{y}{x}\)
\(\alpha = \tan^{-1} \left(\dfrac{y}{x}\right)\dotso\dotso\color{red} \text{ cek kuadran titik}\)
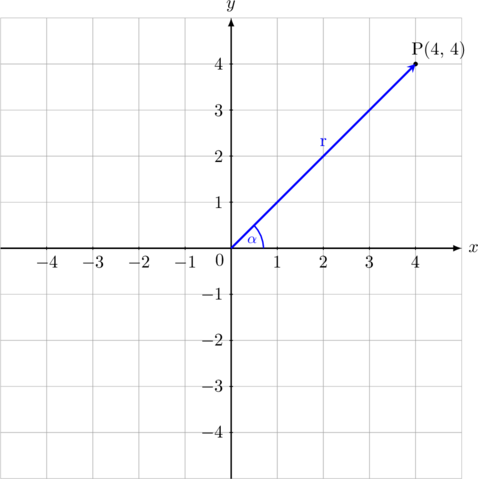
\(r = \sqrt{4^2 + 4^2} = \sqrt{2\cdot 4^2} = 4\sqrt{2}\)
\(\tan \alpha = \dfrac{4}{4} = 1\)
\(\alpha = 45^{\circ}\dotso\dotso \text{ titik (4, 4) di kuadran I}\)
Jadi \(\text{P(4, 4)} = \text{P}(4\sqrt{2}, 45^{\circ})\)
Mengubah Koordinat Polar Menjadi Koordinat Kartesius
Titik \((r, \alpha)\) dapat diubah menjadi koordinat kartesius \((x, y)\)
\(x = r\cdot \cos \alpha\)
\(y = r\cdot \sin \alpha\)
CONTOH SOAL
Soal 1
Tentukan koordinat polar dari titik \(\text{P}(-\sqrt{3}, 1)\)
Soal 2
Tentukan koordinat kartesius dari titik \(\text{P}(5, 300^{\circ})\)