Persamaan lingkaran yang berpusat di titik (0, 0) dan berjari-jari \(r\)
Lingkaran di atas berpusat di titik (0, 0) dan berjari-jari 4.
Persamaan lingkarannya adalah:
\(x^2 + y^2 = 4^2\)
\(x^2 + y^2 = 16\)
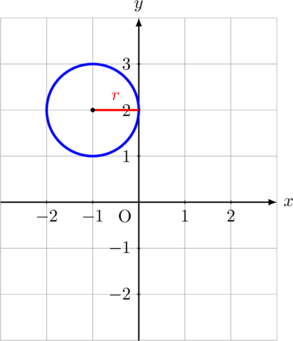
Persamaan lingkaran yang berpusat di titik (a, b) dan berjari-jari \(r\)
Lingkaran di atas berpusat di titik (1, 2) dan berjari-jari 3.
Persamaan lingkarannya adalah:
\((x\:-\:1)^2 + (y\:-\:2)^2 = 3^2\)
\(x^2 \:-\:2x + 1 + y^2 \:-\:4y + 4 = 9\)
\(x^2 + y^2 \:-\:2x\:-\:4y + 5\:-\:9 = 0\)
\(x^2 + y^2 \:-\:2x\:-\:4y \:-\:4 = 0\)
Persamaan lingkaran yang berpusat di titik \(\left(-\dfrac{1}{2}\text{A}, -\dfrac{1}{2}\text{B}\right)\) dan berjari-jari \(\text{R}\)
Soal 2
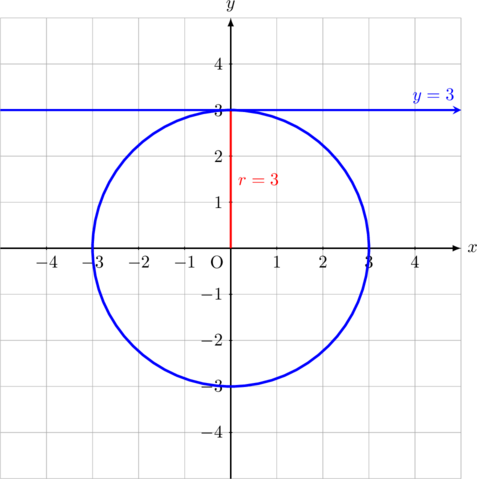
Tentukan persamaan lingkaran yang berpusat di titik (0, 0) dan menyinggung garis \(y = 3\).
Soal 4
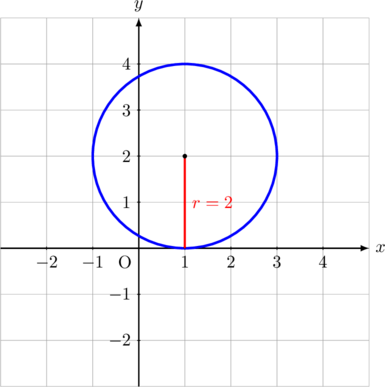
Tentukan persamaan lingkaran yang berpusat di titik (1, 2) dan menyinggung sumbu \(x\).
Panjang jari-jari lingkaran adalah jarak dari pusat lingkaran (0, 1) ke garis \(50x\:-\:47y + 185 = 0\).
\(r = \left|\dfrac{50x_1\:-\:47y_1 + 185 }{\sqrt{50^2 + (-47)^2}}\right|\)
\(r = \left|\dfrac{50(0)\:-\:47(1) + 185 }{\sqrt{2500 + 2209}}\right|\)
\(r = \left|\dfrac{138}{\sqrt{4709}}\right|\)
\(r = \dfrac{138}{\sqrt{4709}}\)
Persamaan lingkaran dengan pusat (0, 1) dan jari-jari \(r = \dfrac{138}{\sqrt{4709}}\) adalah:
\((x\:-\:0)^2 + (y\:-\:1)^2 = \left(\dfrac{138}{\sqrt{4709}}\right)^2\)
\((x\:-\:0)^2 + (y\:-\:1)^2 = \dfrac{19044}{4709}\)
\(x^2 + y^2\:-\:2y + 1 = 4,04\)
\(x^2 + y^2\:-\:2y \:-\:3,04 = 0\)
Soal 7
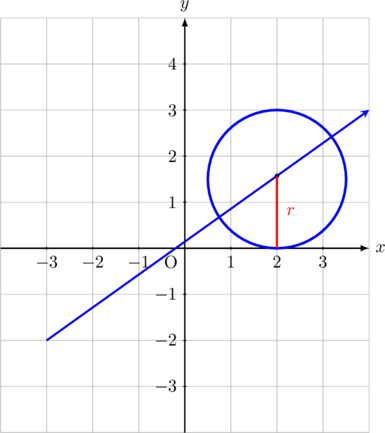
Tentukan persamaan lingkaran yang pusatnya terletak di garis \(5x\:-\:7y + 1 = 0\) dan menyinggung sumbu \(x\) di titik \((2, 0)\).
\(\color{blue} x^2 + y^2 = r^2\)
Contoh Tentukan persamaan lingkaran di bawah ini: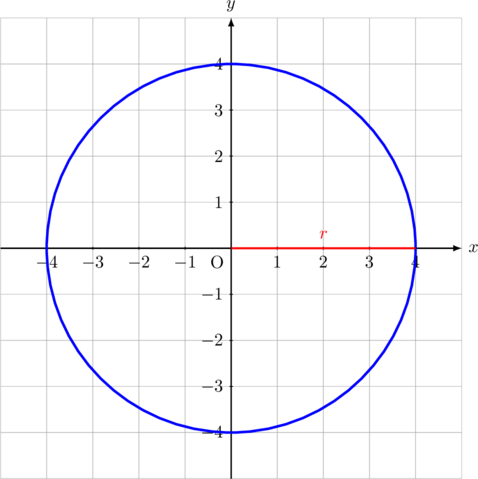
\(\color{blue} (x\:-\:a)^2 + (y\:-\:b)^2 = r^2\)
Contoh Tentukan persamaan lingkaran di bawah ini: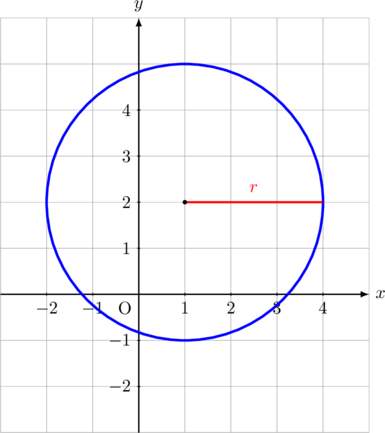
\(\color{blue} x^2 + y^2 + \text{A}x + \text{B}y + C = 0\)
Cara menghitung jari-jari: R = \(\sqrt{(-\frac{1}{2}\text{A})^2 + (-\frac{1}{2}\text{B})^2\:-\:\text{C}}\) R = \(\sqrt{\frac{1}{4}\text{A}^2 +\frac{1}{4}\text{B}^2 \:-\:\text{C}}\) Contoh Tentukan pusat dan jari-jari lingkaran \(x^2 + y^2 \:-\:6x + 4y + 2 = 0\) Nilai \(\text{A} = -6, \text{B} = 4, \text{ dan } \text{C} = 2\) Pusat lingkaran: \((-\frac{1}{2}\text{A}, -\frac{1}{2}\text{B})\) \([-\frac{1}{2}(-6), -\frac{1}{2}(4)]\) \((3, -2)\) Jari-jari lingkaran: R = \(\sqrt{\frac{1}{4}\text{A}^2 + \frac{1}{4}\text{B}^2 \:-\:\text{C}}\) R = \(\sqrt{\frac{1}{4}(-6)^2 + \frac{1}{4}(4)^2 \:-\:2}\) R = \(\sqrt{\frac{1}{4}(36) + \frac{1}{4}(16) \:-\:2}\) R = \(\sqrt{9 + 4 \:-\:2}\) R = \(\sqrt{11}\) atau Karena pusat lingkaran sudah diketahui berada di titik \((3, -2)\), maka jari-jari lingkarannya adalah: R = \(\sqrt{(3)^2 + (-2)^2 \:-\:2}\) R = \(\sqrt{9 + 4 \:-\:2}\) R = \(\sqrt{11}\)Persamaan Parametrik Lingkaran
Persamaan implisit \(x^2 + y^2 = 1\) merupakan persamaan lingkaran berpusat di (0, 0) dengan jari-jari 1. Lingkaran ini juga diidentifikasi dengan persamaan parametrik \(x = \cos \alpha\) \(y = \sin \alpha\) \(0 \leq \alpha \leq 2\pi\) Persamaan parametrik lingkaran yang berpusat di \((a, b)\) dan berjari-jari \(r\) adalah: \(x = a + r \cos \alpha\) \(y = b + r \sin \alpha\) dengan \(0 \leq \alpha \leq 2 \pi\)RUMUS PENTING!
A. Jarak titik ke titik Jarak titik P\((x_1, y_1)\) ke titik Q\((x_2, y_2)\) adalah:\(\color{blue}\text{PQ} = \sqrt{(x_2\:-\:x_1)^2 + (y_2\:-\:y_1)^2}\)
Contoh Tentukan jarak titik P\((6, -5)\) ke titik Q\((0, -13)\). \(\text{PQ} = \sqrt{(0\:-\:6)^2 + (-13\:-\:(-5))^2}\) \(\text{PQ} = \sqrt{(-6)^2 + (-8)^2}\) \(\text{PQ} = \sqrt{36 + 64}\) \(\text{PQ} = \sqrt{100}\) \(\text{PQ} = 10\text{ satuan}\) B. Jarak titik ke garis Jarak titik P\((x_1, y_1)\) ke garis \(ax + by + c = 0\) adalah:\(\color{blue} r = \left|\dfrac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}}\right|\)
Contoh Tentukan jarak titik P\((2, 1)\) ke garis \(3x\:-\:4y + 10 = 0\) \(r = \left|\dfrac{3x_1\:-\:4y_1 + 10}{\sqrt{3^2 + (-4)^2}}\right|\) \(r = \left|\dfrac{3(2)\:-\:4(1) + 10}{\sqrt{9 + 16}}\right|\) \(r = \left|\dfrac{6\:-\:4 + 10}{\sqrt{25}}\right|\) \(r = \left|\dfrac{12}{5}\right|\) \(r = 2\dfrac{2}{5}\text{ satuan}\) C. Titik Tengah Ruas Garis Titik tengah ruas garis PQ, dengan \(\text{P}(x_1, y_1)\) dan \(\text{Q}(x_2, y_2)\) adalah titik M. \(\color{blue}\text{M}\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\) Contoh Tentukan koordinat titik M yang berada di tengah ruas garis PQ, dengan titik \(\text{P}(2, 6)\) dan \(\text{Q}(-4, 10)\) \(\text{M}\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\) \(\text{M}\left(\dfrac{2 + (-4)}{2}, \dfrac{6 +10}{2}\right)\) \(\text{M}\left(\dfrac{-2}{2}, \dfrac{16}{2}\right)\) \(\text{M}(-1, 8)\)CONTOH SOAL
Soal 1 Tentukan persamaan lingkaran yang berpusat di titik (0, 0) dan melalui titik (7, 24).
Jari-jari lingkaran dapat dihitung dengan rumus jarak titik (0, 0) ke titik (7, 24)
\(r = \sqrt{(7\:-\:0)^2 +(24\:-\:0)^2}\)
\(r = \sqrt{7^2 + 24^2}\)
\(r = \sqrt{49 + 576}\)
\(r = \sqrt{625} = 25\)
Persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari 25 adalah:
\(x^2 + y^2 = 25^2\)
\(x^2 + y^2 = 625\)
Karena lingkaran berpusat di (0, 0) dan menyinggung garis \(y = 3\), maka jari-jari lingkaran adalah 3
Persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari 3 adalah:
\(x^2 + y^2 = 3^2\)
\(x^2 + y^2 = 9\)
Soal 3
Tentukan persamaan lingkaran yang memiliki diameter PQ, dengan titik \(\text{P}(-3, 5)\) dan \(\text{Q}(7, 15)\)
Pusat lingkaran terletak di tengah-tengah ruas garis PQ
\(\text{O}\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
\(\text{O}\left(\dfrac{-3 + 7}{2}, \dfrac{5 + 15}{2}\right)\)
\(\text{O}(2, 10)\)
Jari-jari lingkaran dapat dicari dengan menggunakan rumus jarak dua titik
Jari-jari adalah jarak antara titik pusat (2, 10) ke titik (-3, 5)
\(r = \sqrt{(x_2 \:-\:x_1)^2 + (y_2 \:-\:y_1)^2}\)
\(r = \sqrt{(-3\:-\:2)^2 + (5\:-\:10)^2}\)
\(r = \sqrt{(-5)^2 + (-5)^2}\)
\(r = \sqrt{50}\)
Persamaan lingkaran yang berpusat di titik (2, 10) dan berjari-jari \(\sqrt{50}\) adalah:
\((x\:-\:a)^2 + (y\:-\:b)^2 = r^2\)
\((x\:-\:2)^2 + (y\:-\:10)^2 = 50\)
Karena lingkaran berpusat di (1, 2) dan menyinggung sumbu \(x\), maka panjang jari-jari lingkarannya sama dengan 2.
Persamaan lingkaran yang berpusat di titik (1, 2) dan berjari-jari 2 adalah:
\((x\:-\:1)^2 + (y\:-\:2)^2 = 2^2\)
\(x^2 \:-\:2x + 1 + y^2 \:-\:4y + 4 = 4\)
\(x^2 + y^2 \:-\:2x \:-\:4y + 1 = 0\)
Soal 5
Tentukan persamaan lingkaran yang berpusat di titik (-1, 2) dan menyinggung sumbu \(y\).
Karena lingkaran berpusat di (-1, 2) dan menyinggung sumbu \(y\), maka panjang jari-jari lingkarannya sama dengan 1.
Persamaan lingkaran yang berpusat di titik (-1, 2) dan berjari-jari 1 adalah:
\([x\:-\:(-1)]^2 + (y\:-\:2)^2 = 1^2\)
\((x + 1)^2 + (y\:-\:2)^2 = 1\)
\(x^2 + 2x + 1 + y^2 \:-\:4y + 4 = 1\)
\(x^2 + y^2 + 2x \:-\:4y + 4 = 0\)
Soal 6
Tentukan persamaan lingkaran yang berpusat di titik (0, 1) dan menyinggung garis \(50x\:-\:47y + 185 = 0\).
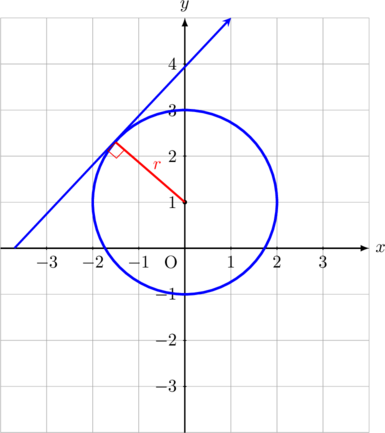
Perhatikan gambar berikut:
Dari gambar di atas, dapat diketahui bahwa pusat lingkaran berada di \(x = 2\), karena pusat lingkaran berada pada garis \(5x\:-\:7y + 1 = 0\), maka berlaku:
\(5(2)\:-\:7y + 1 = 0\)
\(10\:-\:7y + 1 = 0\)
\(11 = 7y\)
\(y = \frac{11}{7}\)
Pusat lingkaran berada di titik \((2, \frac{11}{7})\)
Jari-jari lingkaran adalah \(\frac{11}{7}\)
Persamaan lingkarannya adalah:
\((x\:-\:2)^2 + (y\:-\:\frac{11}{7})^2 = (\frac{11}{7})^2\)
\(x^2 \:-\:4x + 4 + y^2 \:-\:\frac{22}{7}y + \frac{121}{49} = \frac{121}{49}\)
\(x^2 + y^2 \:-\:4x \:-\:\frac{22}{7}y + 4 = 0\)
Soal 8
Diketahui lingkaran \(2x^2 + 2y^2 \:-\:8x\:-\:my + 2 = 0\) melalui titik \((0, 1)\). Tentukan pusat dan jari-jari lingkaran tersebut.
Substitusikan titik \((0, 1)\) ke persamaan lingkaran \(2x^2 + 2y^2 \:-\:8x\:-\:my + 2 = 0\)
\(2(0)^2 + 2(1)^2 \:-\:8(0)\:-\:m(1) + 2 = 0\)
\(0 + 2 \:-\:0\:-\:m + 2 = 0\)
\(m = 4\)
Bagi persamaan lingkaran dengan 2, agar koefisien \(x^2\) dan \(y^2\) sama dengan 1
\(2x^2 + 2y^2 \:-\:8x\:-\:4y + 2 = 0\)
\(x^2 + y^2 \:-\:4x\:-\:2y + 1= 0\)
\(\text{A} = -4, \text{B} = -2, \text{ dan } \text{C} = 1\)
Pusat lingkaran:
\([-\frac{1}{2}(-4), -\frac{1}{2}(-2)]\)
\((2, 1)\)
Jari-jari lingkaran:
R = \(\sqrt{2^2 + 1^2\:-\:2}\)
R = \(\sqrt{3}\)
