Garis Kuasa dan Titik Kuasa

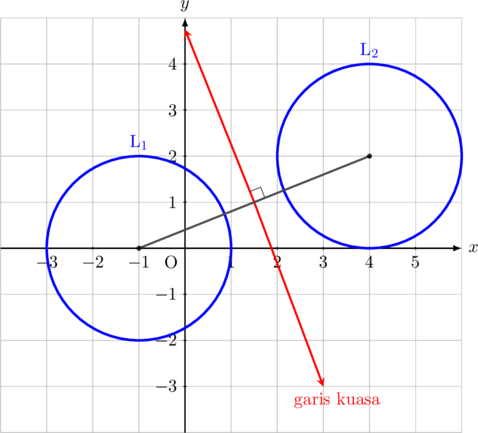
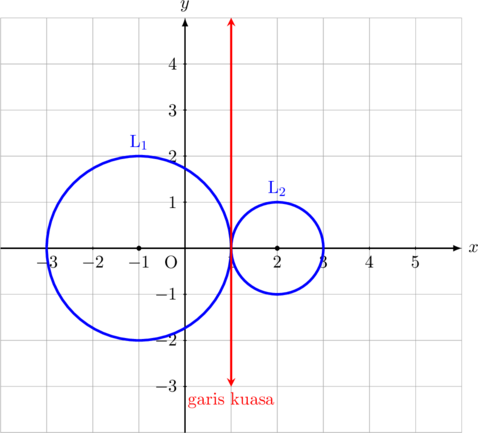
Garis kuasa antara dua lingkaran terbentuk dari himpunan titik-titik yang memiliki kuasa yang sama terhadap kedua lingkaran tersebut. Garis kuasa tegak lurus dengan garis hubung kedua pusat lingkaran. Misal persamaan lingkaran pertama adalah \(\textbf{L}_1\) dan persamaan lingkaran kedua adalah \(\textbf{L}_2\), maka persamaan garis kuasa kedua lingkaran tersebut adalah:

\(\color{blue} \textbf{L}_1 \:-\:\textbf{L}_2 = 0\)

   

Titik Kuasa 

Jika titik A memiliki kuasa yang sama terhadap 3 buah lingkaran yaitu \(\textbf{L}_1, \textbf{L}_2, \text{ dan } \textbf{L}_3\), maka akan memenuhi:

\(\color{blue} \textbf{L}_1 = \textbf{L}_2 = \textbf{L}_3\)

Untuk mendapatkan titik A tersebut eliminasi dua persamaan garis kuasa berikut:

\(\textbf{L}_1 \:-\:\textbf{L}_2 = 0\dotso\dotso \color{blue} (1)\)

\(\textbf{L}_2 \:-\:\textbf{L}_3 = 0\dotso\dotso \color{blue} (2)\)

   

CONTOH SOAL

  Soal 1 Tentukan persamaan garis yang memiliki kuasa yang sama terhadap 2 lingkaran berikut: \(\textbf{L}_1 : x^2 + y^2 + 2x + 4y \:-\:10 = 0\) \(\textbf{L}_2 : x^2 + y^2 \:-\: 5x + 3y + 14 = 0\)   Soal 2 Tentukan titik yang memiliki kuasa yang sama terhadap 3 lingkaran berikut: \(\textbf{L}_1 : x^2 + y^2 \:-\: 3x + y \:-\:4 = 0\) \(\textbf{L}_2 : x^2 + y^2 + 5x + 5y + 10 = 0\) \(\textbf{L}_3 : x^2 + y^2 \:-\: 2x + 2y + 6 = 0\)