Quiz-summary
0 of 13 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 45 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 13 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 13
1. Pertanyaan
1 pointsDiketahui koordinat titik A\((-1, 2, 0)\) dan titik B\((3, -4, 2)\). Vektor satuan dari \(\overrightarrow{\text{BA}}\) adalah …
Benar
\(\widehat{\text{BA}}=\dfrac{\textbf{BA}}{||\textbf{BA}||}\)
\(\overrightarrow{\text{BA}} = \textbf{a}\:-\:\textbf{b}\)
\(\overrightarrow{\text{BA}} = \left(\begin{array}{c}-1\\ 2\\0\end{array}\right)\:-\:\left(\begin{array}{c}3\\-4\\2\end{array}\right)\)
\(\overrightarrow{\text{BA}} = \left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{(-4)^2 + 6^2 + (-2)^2}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{16 + 36 + 4}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{56}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{2\sqrt{14}}\)
\(\widehat{\text{BA}}=\dfrac{1}{\sqrt{14}}\left(\begin{array}{c}-2\\ 3\\-1\end{array}\right)\)
Salah
\(\widehat{\text{BA}}=\dfrac{\textbf{BA}}{||\textbf{BA}||}\)
\(\overrightarrow{\text{BA}} = \textbf{a}\:-\:\textbf{b}\)
\(\overrightarrow{\text{BA}} = \left(\begin{array}{c}-1\\ 2\\0\end{array}\right)\:-\:\left(\begin{array}{c}3\\-4\\2\end{array}\right)\)
\(\overrightarrow{\text{BA}} = \left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{(-4)^2 + 6^2 + (-2)^2}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{16 + 36 + 4}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{\sqrt{56}}\)
\(\widehat{\text{BA}}=\dfrac{\left(\begin{array}{c}-4\\ 6\\-2\end{array}\right)}{2\sqrt{14}}\)
\(\widehat{\text{BA}}=\dfrac{1}{\sqrt{14}}\left(\begin{array}{c}-2\\ 3\\-1\end{array}\right)\)
-
Pertanyaan 2 dari 13
2. Pertanyaan
1 pointsDiketahui \(\textbf{u} = 2\textbf{i} \:-\:5\textbf{j} + \textbf{k}\) dan \(\textbf{v} = \textbf{j} + 3\textbf{k}\). Pernyataan di bawah ini yang benar adalah …
Benar
\(\textbf{u} = 2\textbf{i} \:-\:5\textbf{j} + \textbf{k}\)
\(||\textbf{u}|| = \sqrt{2^2 + (-5)^2 + 1^2}\)
\(||\textbf{u}|| = \sqrt{4 + 25 + 1}\)
\(||\textbf{u}|| = \sqrt{30}\)
\(\textbf{v} = \textbf{j} + 3\textbf{k}\)
\(||\textbf{v}|| = \sqrt{1^2 + 3^2}\)
\(||\textbf{v}|| = \sqrt{1 + 9}\)
\(||\textbf{v}|| = \sqrt{10}\)
\(||\textbf{u}|| \cdot ||\textbf{v}|| =\sqrt{30}\cdot \sqrt{10} = 10\sqrt{3}\)
\(||\textbf{u}||\:-\: ||\textbf{v}|| =\sqrt{30}\:-\: \sqrt{10}\)
\(\textbf{u}\:-\:2\textbf{v} = 2\textbf{i} \:-\:5\textbf{j} + \textbf{k}\:-\:(\textbf{j} + 3\textbf{k})\)
\(\textbf{u}\:-\:2\textbf{v} = 2\textbf{i} \:-\:7\textbf{j} \:-\:5\textbf{k})\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{2^2 + (-7)^2 + (-5)^2}\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{4 + 49 + 25}\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{78}\)
Salah
\(\textbf{u} = 2\textbf{i} \:-\:5\textbf{j} + \textbf{k}\)
\(||\textbf{u}|| = \sqrt{2^2 + (-5)^2 + 1^2}\)
\(||\textbf{u}|| = \sqrt{4 + 25 + 1}\)
\(||\textbf{u}|| = \sqrt{30}\)
\(\textbf{v} = \textbf{j} + 3\textbf{k}\)
\(||\textbf{v}|| = \sqrt{1^2 + 3^2}\)
\(||\textbf{v}|| = \sqrt{1 + 9}\)
\(||\textbf{v}|| = \sqrt{10}\)
\(||\textbf{u}|| \cdot ||\textbf{v}|| =\sqrt{30}\cdot \sqrt{10} = 10\sqrt{3}\)
\(||\textbf{u}||\:-\: ||\textbf{v}|| =\sqrt{30}\:-\: \sqrt{10}\)
\(\textbf{u}\:-\:2\textbf{v} = 2\textbf{i} \:-\:5\textbf{j} + \textbf{k}\:-\:(\textbf{j} + 3\textbf{k})\)
\(\textbf{u}\:-\:2\textbf{v} = 2\textbf{i} \:-\:7\textbf{j} \:-\:5\textbf{k})\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{2^2 + (-7)^2 + (-5)^2}\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{4 + 49 + 25}\)
\(||\textbf{u}\:-\:2\textbf{v} || = \sqrt{78}\)
-
Pertanyaan 3 dari 13
3. Pertanyaan
1 pointsJika \(\textbf{p} = \left(\begin{array}{c}1\\ 3\\0\end{array}\right)\), \(\textbf{q} = \left(\begin{array}{c}0\\ -1\\2\end{array}\right)\) dan \(\textbf{r} = \left(\begin{array}{c}1\\ 3\\-3\end{array}\right)\), maka nilai \(||(2\textbf{p} + \textbf{q})\:-\:(\textbf{p}\:-\:3\textbf{r})|| = \dotso\)
Benar
\(2\textbf{p} + \textbf{q}\:-\:(\textbf{p}\:-\:3\textbf{r})\)
\(2\textbf{p} + \textbf{q}\:-\:\textbf{p}+ 3\textbf{r}\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r}\)
\(\left(\begin{array}{c}1\\ 3\\0\end{array}\right) + \left(\begin{array}{c}0\\ -1\\2\end{array}\right) + 3\left(\begin{array}{c}1\\ 3\\-3\end{array}\right)\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r} = \left(\begin{array}{c}1 + 0 + 3\\3\:-\:1 + 9\\0 + 2 \:-\:9\end{array}\right)\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r} = \left(\begin{array}{c}4\\11\\-7\end{array}\right)\)
\(||\textbf{p} + \textbf{q}+ 3\textbf{r} ||= \sqrt{4^2 + 11^2 + (-7)^2}\)
\(\sqrt{16 + 121 +49}\)
\(\sqrt{186}\)
Salah
\(2\textbf{p} + \textbf{q}\:-\:(\textbf{p}\:-\:3\textbf{r})\)
\(2\textbf{p} + \textbf{q}\:-\:\textbf{p}+ 3\textbf{r}\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r}\)
\(\left(\begin{array}{c}1\\ 3\\0\end{array}\right) + \left(\begin{array}{c}0\\ -1\\2\end{array}\right) + 3\left(\begin{array}{c}1\\ 3\\-3\end{array}\right)\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r} = \left(\begin{array}{c}1 + 0 + 3\\3\:-\:1 + 9\\0 + 2 \:-\:9\end{array}\right)\)
\(\textbf{p} + \textbf{q}+ 3\textbf{r} = \left(\begin{array}{c}4\\11\\-7\end{array}\right)\)
\(||\textbf{p} + \textbf{q}+ 3\textbf{r} ||= \sqrt{4^2 + 11^2 + (-7)^2}\)
\(\sqrt{16 + 121 +49}\)
\(\sqrt{186}\)
-
Pertanyaan 4 dari 13
4. Pertanyaan
1 pointsDiketahui titik A\((2, 0, -6)\) dan titik B\((-4, 2, 4)\). Titik P terletak di tengah-tengah AB. Vektor posisi dari P adalah …
Benar
\(\textbf{p} = \dfrac{\textbf{a} + \textbf{b}}{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}2\\ 0\\-6\end{array}\right) + \left(\begin{array}{c}-4\\ 2\\4\end{array}\right)}{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}2\:-\:4\\ 0 + 2\\-6 + 4\end{array}\right) }{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}-2\\2\\-2\end{array}\right) }{2}\)
\(\textbf{p} = \left(\begin{array}{c}-1\\1\\-1\end{array}\right)\)
Salah
\(\textbf{p} = \dfrac{\textbf{a} + \textbf{b}}{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}2\\ 0\\-6\end{array}\right) + \left(\begin{array}{c}-4\\ 2\\4\end{array}\right)}{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}2\:-\:4\\ 0 + 2\\-6 + 4\end{array}\right) }{2}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}-2\\2\\-2\end{array}\right) }{2}\)
\(\textbf{p} = \left(\begin{array}{c}-1\\1\\-1\end{array}\right)\)
-
Pertanyaan 5 dari 13
5. Pertanyaan
1 pointsDiketahui A\((3, 7)\) dan titik B\((3, 3)\). Titik P terletak pada ruas garis AB, dengan perbandingan AP : PB = 1 : 3. Vektor posisi titik P tersebut ditulis dalam vektor basis adalah …
Benar
\(\textbf{p} = \dfrac{1\cdot \textbf{b} + 3\cdot \textbf{a}}{1 + 3}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}3\\3\end{array}\right)+ 3\left(\begin{array}{c}3\\7\end{array}\right)}{4}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}3 + 9\\3 + 21\end{array}\right)}{4}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}12\\24\end{array}\right)}{4}\)
\(\textbf{p} = \left(\begin{array}{c}3\\6\end{array}\right)\)
\(\textbf{p} =3\textbf{i} + 6\textbf{j}\)
Salah
\(\textbf{p} = \dfrac{1\cdot \textbf{b} + 3\cdot \textbf{a}}{1 + 3}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}3\\3\end{array}\right)+ 3\left(\begin{array}{c}3\\7\end{array}\right)}{4}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}3 + 9\\3 + 21\end{array}\right)}{4}\)
\(\textbf{p} = \dfrac{\left(\begin{array}{c}12\\24\end{array}\right)}{4}\)
\(\textbf{p} = \left(\begin{array}{c}3\\6\end{array}\right)\)
\(\textbf{p} =3\textbf{i} + 6\textbf{j}\)
-
Pertanyaan 6 dari 13
6. Pertanyaan
1 pointsTitik A\((3, 0, -6)\), B\((3, -12, 0)\) dan P kolinear dengan perbandingan AP : PB = – 2 : 5. Jika \(\textbf{p}\) adalah vektor posisi dari titik P, maka \(\textbf{p} = \dotso\)
Benar
\(\dfrac{\overrightarrow{\text{AP}}}{\overrightarrow{\text{PB}}} = \dfrac{- 2}{5}\)
\(\dfrac{\textbf{p}\:-\:\textbf{a}}{\textbf{b}\:-\:\textbf{p}} = -2 : 5\)
\(5\textbf{p}\:-\:5\textbf{a} = -2\textbf{b} + 2\textbf{p}\)
\(5\textbf{p}\:-\:2\textbf{p} = 5\textbf{a}\:-\:2\textbf{b}\)
\(3\textbf{p} = 5\textbf{a}\:-\:2\textbf{b}\)
\(\textbf{p} = \dfrac{5}{3}\textbf{a}\:-\:\dfrac{2}{3}\textbf{b}\)
\(\textbf{p} = \dfrac{5}{3}\left(\begin{array}{c}3\\0\\-6\end{array}\right)\:-\:\dfrac{2}{3}\left(\begin{array}{c}3\\-12\\0\end{array}\right)\)
\(\textbf{p} = \left(\begin{array}{c}5\\0\\-10\end{array}\right)\:-\:\left(\begin{array}{c}2\\-8\\0\end{array}\right)\)
\(\textbf{p} = \left(\begin{array}{c}3\\8\\-10\end{array}\right)\)
Salah
\(\dfrac{\overrightarrow{\text{AP}}}{\overrightarrow{\text{PB}}} = \dfrac{- 2}{5}\)
\(\dfrac{\textbf{p}\:-\:\textbf{a}}{\textbf{b}\:-\:\textbf{p}} = -2 : 5\)
\(5\textbf{p}\:-\:5\textbf{a} = -2\textbf{b} + 2\textbf{p}\)
\(5\textbf{p}\:-\:2\textbf{p} = 5\textbf{a}\:-\:2\textbf{b}\)
\(3\textbf{p} = 5\textbf{a}\:-\:2\textbf{b}\)
\(\textbf{p} = \dfrac{5}{3}\textbf{a}\:-\:\dfrac{2}{3}\textbf{b}\)
\(\textbf{p} = \dfrac{5}{3}\left(\begin{array}{c}3\\0\\-6\end{array}\right)\:-\:\dfrac{2}{3}\left(\begin{array}{c}3\\-12\\0\end{array}\right)\)
\(\textbf{p} = \left(\begin{array}{c}5\\0\\-10\end{array}\right)\:-\:\left(\begin{array}{c}2\\-8\\0\end{array}\right)\)
\(\textbf{p} = \left(\begin{array}{c}3\\8\\-10\end{array}\right)\)
-
Pertanyaan 7 dari 13
7. Pertanyaan
1 points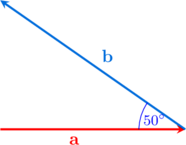
Besar sudut antara vektor \(\textbf{a}\) dan \(\textbf{b}\) di atas adalah …
Benar
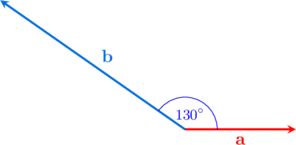 Salah
Salah

-
Pertanyaan 8 dari 13
8. Pertanyaan
1 pointsMisalkan ABCD adalah segi empat dengan diagonal AC dan BD berpotongan di titik P. Jika DP = PB dan AP = 2PC, \(\overrightarrow{\text{AB}} = \textbf{a}\) dan \(\overrightarrow{\text{AD}} = \textbf{b}\), maka \(\overrightarrow{\text{PC}} = \dotso\)
Benar
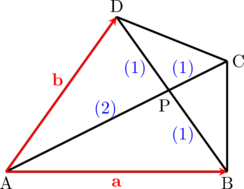
Langkah 1 Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{BP}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{a} + \textbf{b}\)
\(\overrightarrow{\text{BP}} = \dfrac{1}{2}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{BP}} = -\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
Langkah 2 Menentukan \(\overrightarrow{\text{AP}}\)
\(\overrightarrow{\text{AP}} = \overrightarrow{\text{AB}} +\overrightarrow{\text{BP}}\)
\(\overrightarrow{\text{AP}} = \textbf{a} \:-\:\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
\(\overrightarrow{\text{AP}} = \dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
Langkah 3 Menentukan \(\overrightarrow{\text{PC}}\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{2}\overrightarrow{\text{AP}}\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{2}\left[\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\right]\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{4}\textbf{a} + \dfrac{1}{4}\textbf{b}\)
Salah

Langkah 1 Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{BP}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{a} + \textbf{b}\)
\(\overrightarrow{\text{BP}} = \dfrac{1}{2}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{BP}} = -\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
Langkah 2 Menentukan \(\overrightarrow{\text{AP}}\)
\(\overrightarrow{\text{AP}} = \overrightarrow{\text{AB}} +\overrightarrow{\text{BP}}\)
\(\overrightarrow{\text{AP}} = \textbf{a} \:-\:\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
\(\overrightarrow{\text{AP}} = \dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\)
Langkah 3 Menentukan \(\overrightarrow{\text{PC}}\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{2}\overrightarrow{\text{AP}}\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{2}\left[\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\right]\)
\(\overrightarrow{\text{PC}} = \dfrac{1}{4}\textbf{a} + \dfrac{1}{4}\textbf{b}\)
-
Pertanyaan 9 dari 13
9. Pertanyaan
1 pointsPerhatikan gambar berikut:

ABCD adalah sebuah persegi panjang dan ABEC adalah sebuah jajargenjang. Jika \(\overrightarrow{\text{AB}} = \textbf{u}\) dan \(\overrightarrow{\text{AD}} = \textbf{v}\), maka \(\overrightarrow{\text{AE}} +\overrightarrow{\text{OD}} = \dotso\)
Benar
Langkah 1: Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{OD}} = \dfrac{1}{2}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{OD}} = \dfrac{1}{2}(-\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{OD}} = -\dfrac{1}{2}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
Langkah 2: Menentukan \(\overrightarrow{\text{AC}}\) dan \(\overrightarrow{\text{BE}}\)
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}} = \textbf{u} + \textbf{v}\)
Karena ABEC adalah jajargenjang maka:
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{BE}} = \textbf{u} + \textbf{v}\)
Langkah 3: Menentukan \(\overrightarrow{\text{AE}}\)
\(\overrightarrow{\text{AE}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BE}}\)
\(\overrightarrow{\text{AE}} = \textbf{u} + \textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{AE}} = 2\textbf{u} + \textbf{v}\)
Langkah 4: Menentukan \(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}} = 2\textbf{u} + \textbf{v} + -\dfrac{1}{2}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
\(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}} = \dfrac{3}{2}\textbf{u} + \dfrac{3}{2}\textbf{v}\)
Salah
Langkah 1: Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{OD}} = \dfrac{1}{2}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{OD}} = \dfrac{1}{2}(-\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{OD}} = -\dfrac{1}{2}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
Langkah 2: Menentukan \(\overrightarrow{\text{AC}}\) dan \(\overrightarrow{\text{BE}}\)
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}} = \textbf{u} + \textbf{v}\)
Karena ABEC adalah jajargenjang maka:
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{BE}} = \textbf{u} + \textbf{v}\)
Langkah 3: Menentukan \(\overrightarrow{\text{AE}}\)
\(\overrightarrow{\text{AE}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BE}}\)
\(\overrightarrow{\text{AE}} = \textbf{u} + \textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{AE}} = 2\textbf{u} + \textbf{v}\)
Langkah 4: Menentukan \(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}} = 2\textbf{u} + \textbf{v} + -\dfrac{1}{2}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
\(\overrightarrow{\text{AE}} + \overrightarrow{\text{OD}} = \dfrac{3}{2}\textbf{u} + \dfrac{3}{2}\textbf{v}\)
-
Pertanyaan 10 dari 13
10. Pertanyaan
1 pointsDiketahui \(\textbf{p} = \left(\begin{array}{c}9\\4\\5\end{array}\right)\), \(\textbf{q} = \left(\begin{array}{c}3\\-2\\3\end{array}\right)\) dan \(\textbf{r} = \left(\begin{array}{c}0\\5\\-2\end{array}\right)\). Jika ketiga vektor tersebut satu bidang sehingga dapat dinyatakan \(\textbf{p} = m\textbf{q} + n\textbf{r}\), maka nilai \(m + n = \dotso\)
Benar
\(\textbf{p} = m\textbf{q} + n\textbf{r}\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = m\left(\begin{array}{c}3\\-2\\3\end{array}\right) + n\left(\begin{array}{c}0\\5\\-2\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m\\3m\end{array}\right) + \left(\begin{array}{c}0\\5n\\-2n\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m + 5n\\3m\:-\:2n\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m + 5n\\3m\:-\:2n\end{array}\right)\)
Dengan prinsip kesamaan dua vektor:
\(9 = 3m\rightarrow m = 3\)
\(4 = -2m + 5n\)
\(4 = -2(3) + 5n\)
\(4 = -6 + 5n\)
\(4 + 6 = 5n\)
\(10 = 5n\)
\(n = 2\)
Jadi, \(m + n = 3 + 2 = 5\)
Salah
\(\textbf{p} = m\textbf{q} + n\textbf{r}\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = m\left(\begin{array}{c}3\\-2\\3\end{array}\right) + n\left(\begin{array}{c}0\\5\\-2\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m\\3m\end{array}\right) + \left(\begin{array}{c}0\\5n\\-2n\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m + 5n\\3m\:-\:2n\end{array}\right)\)
\(\left(\begin{array}{c}9\\4\\5\end{array}\right) = \left(\begin{array}{c}3m\\-2m + 5n\\3m\:-\:2n\end{array}\right)\)
Dengan prinsip kesamaan dua vektor:
\(9 = 3m\rightarrow m = 3\)
\(4 = -2m + 5n\)
\(4 = -2(3) + 5n\)
\(4 = -6 + 5n\)
\(4 + 6 = 5n\)
\(10 = 5n\)
\(n = 2\)
Jadi, \(m + n = 3 + 2 = 5\)
-
Pertanyaan 11 dari 13
11. Pertanyaan
1 pointsPerhatikan jajargenjang ABCD di bawah ini:
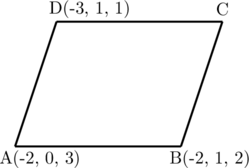
Jika koordinat titik A\((-2, 0, 3)\), B\((-2, 1, 2)\) dan D\((-3, 1, 1)\), maka \(\overrightarrow{\text{AC}}=\dotso\)
Benar
Langkah 1: Menentukan \(\overrightarrow{\text{AD}}\) dan \(\overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AD}}= \textbf{d}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-3\\1\\1\end{array}\right)\:-\:\left(\begin{array}{c}-2\\0\\3\end{array}\right)\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-3\:-\:(-2)\\1\:-\:0\\1\:-\:3\end{array}\right)\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
Karena ABCD jajargenjang, maka:
\(\overrightarrow{\text{AD}}= \overrightarrow{\text{BC}} = \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
Langkah 2: Menentukan \(\overrightarrow{\text{AB}}\)
\(\overrightarrow{\text{AB}}= \textbf{b}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AB}}= \left(\begin{array}{c}-2\\1\\2\end{array}\right)\:-\:\left(\begin{array}{c}-2\\0\\3\end{array}\right)\)
\(\overrightarrow{\text{AB}}= \left(\begin{array}{c}0\\1\\-1\end{array}\right)\)
Langkah 3: Menentukan \(\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{AC}}= \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}}= \left(\begin{array}{c}0\\1\\-1\end{array}\right) + \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
\(\overrightarrow{\text{AC}}= \left(\begin{array}{c}-1\\2\\-3\end{array}\right) \)
\(\overrightarrow{\text{AC}}= -\textbf{i} + 2\textbf{j} \:-\: 3\textbf{k}\)
Salah
Langkah 1: Menentukan \(\overrightarrow{\text{AD}}\) dan \(\overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AD}}= \textbf{d}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-3\\1\\1\end{array}\right)\:-\:\left(\begin{array}{c}-2\\0\\3\end{array}\right)\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-3\:-\:(-2)\\1\:-\:0\\1\:-\:3\end{array}\right)\)
\(\overrightarrow{\text{AD}}= \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
Karena ABCD jajargenjang, maka:
\(\overrightarrow{\text{AD}}= \overrightarrow{\text{BC}} = \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
Langkah 2: Menentukan \(\overrightarrow{\text{AB}}\)
\(\overrightarrow{\text{AB}}= \textbf{b}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AB}}= \left(\begin{array}{c}-2\\1\\2\end{array}\right)\:-\:\left(\begin{array}{c}-2\\0\\3\end{array}\right)\)
\(\overrightarrow{\text{AB}}= \left(\begin{array}{c}0\\1\\-1\end{array}\right)\)
Langkah 3: Menentukan \(\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{AC}}= \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}}= \left(\begin{array}{c}0\\1\\-1\end{array}\right) + \left(\begin{array}{c}-1\\1\\-2\end{array}\right)\)
\(\overrightarrow{\text{AC}}= \left(\begin{array}{c}-1\\2\\-3\end{array}\right) \)
\(\overrightarrow{\text{AC}}= -\textbf{i} + 2\textbf{j} \:-\: 3\textbf{k}\)
-
Pertanyaan 12 dari 13
12. Pertanyaan
1 points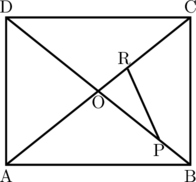
ABCD adalah sebuah persegi panjang. AC dan BD merupakan diagonal persegi panjang yang berpotongan di titik O. Titik R terletak pada AC dengan perbandingan AR : RC = 5 : 3 dan titik P berada pada OB dengan perbandingan BP : PO = 1 : 3. Jika \(\overrightarrow{\text{AB}} = \textbf{u}\) dan \(\overrightarrow{\text{AD}} = \textbf{v}\), maka \(\overrightarrow{\text{PR}}\) dapat dinyatakan sebagai …
Benar
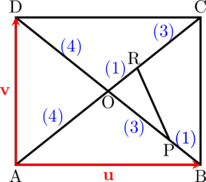
Langkah 1: Menentukan \(\overrightarrow{\text{AC}}\) dan \(\overrightarrow{\text{OR}}\)
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}} = \textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}(\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}\textbf{u} + \dfrac{1}{8}\textbf{v}\)
Langkah 2: Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{PO}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{PO}} = \dfrac{3}{8}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{PO}} = \dfrac{3}{8}(-\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{PO}} = -\dfrac{3}{8}\textbf{u} + \dfrac{3}{8}\textbf{v}\)
Langkah 3: Menentukan \(\overrightarrow{\text{PR}}\)
\(\overrightarrow{\text{PR}} = \overrightarrow{\text{PO}} + \overrightarrow{\text{OR}}\)
\(\overrightarrow{\text{PR}} = -\dfrac{3}{8}\textbf{u} + \dfrac{3}{8}\textbf{v} + \dfrac{1}{8}\textbf{u} + \dfrac{1}{8}\textbf{v}\)
\(\overrightarrow{\text{PR}} = -\dfrac{2}{8}\textbf{u} + \dfrac{4}{8}\textbf{v}\)
\(\overrightarrow{\text{PR}} = -\dfrac{1}{4}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
Salah

Langkah 1: Menentukan \(\overrightarrow{\text{AC}}\) dan \(\overrightarrow{\text{OR}}\)
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}} = \textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}(\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{OR}} = \dfrac{1}{8}\textbf{u} + \dfrac{1}{8}\textbf{v}\)
Langkah 2: Menentukan \(\overrightarrow{\text{BD}}\) dan \(\overrightarrow{\text{PO}}\)
\(\overrightarrow{\text{BD}} = \overrightarrow{\text{BA}} + \overrightarrow{\text{AD}}\)
\(\overrightarrow{\text{BD}} = -\textbf{u} + \textbf{v}\)
\(\overrightarrow{\text{PO}} = \dfrac{3}{8}\overrightarrow{\text{BD}}\)
\(\overrightarrow{\text{PO}} = \dfrac{3}{8}(-\textbf{u} + \textbf{v})\)
\(\overrightarrow{\text{PO}} = -\dfrac{3}{8}\textbf{u} + \dfrac{3}{8}\textbf{v}\)
Langkah 3: Menentukan \(\overrightarrow{\text{PR}}\)
\(\overrightarrow{\text{PR}} = \overrightarrow{\text{PO}} + \overrightarrow{\text{OR}}\)
\(\overrightarrow{\text{PR}} = -\dfrac{3}{8}\textbf{u} + \dfrac{3}{8}\textbf{v} + \dfrac{1}{8}\textbf{u} + \dfrac{1}{8}\textbf{v}\)
\(\overrightarrow{\text{PR}} = -\dfrac{2}{8}\textbf{u} + \dfrac{4}{8}\textbf{v}\)
\(\overrightarrow{\text{PR}} = -\dfrac{1}{4}\textbf{u} + \dfrac{1}{2}\textbf{v}\)
-
Pertanyaan 13 dari 13
13. Pertanyaan
1 pointsPerhatikan gambar kubus OABC.DEFG di bawah ini:
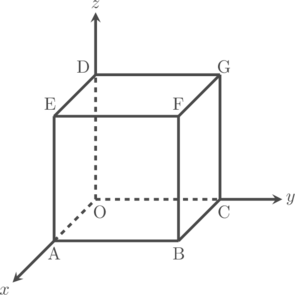
Titik P terletak pada rusuk FG, sehingga FP : PG = 1 : 2. Jika \(\overrightarrow{\text{OA}} = \textbf{u}\), \(\overrightarrow{\text{OC}} = \textbf{v}\) dan \(\overrightarrow{\text{OD}} = \textbf{w}\), maka \(\overrightarrow{\text{OP}} = \dotso\)
Benar
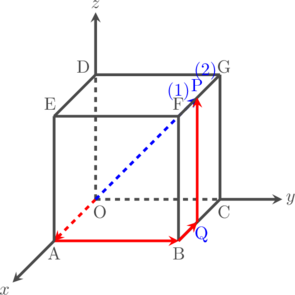
\(\overrightarrow{\text{OP}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AB}} + \overrightarrow{\text{BQ}} + \overrightarrow{\text{QP}}\)
\(\overrightarrow{\text{OP}} = \textbf{u} + \textbf{v} \:-\: \dfrac{1}{3}\textbf{u} + \textbf{w}\)
\(\overrightarrow{\text{OP}} = \dfrac{2}{3}\textbf{u} + \textbf{v} + \textbf{w}\)
Salah

\(\overrightarrow{\text{OP}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AB}} + \overrightarrow{\text{BQ}} + \overrightarrow{\text{QP}}\)
\(\overrightarrow{\text{OP}} = \textbf{u} + \textbf{v} \:-\: \dfrac{1}{3}\textbf{u} + \textbf{w}\)
\(\overrightarrow{\text{OP}} = \dfrac{2}{3}\textbf{u} + \textbf{v} + \textbf{w}\)
