Quiz-summary
0 of 7 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 30 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 7 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 7
1. Pertanyaan
1 pointsHimpunan penyelesaian pertidaksamaan \((4x^2\:-\:9)(4x^2\:-\:8x \:-\:21) > 0\) adalah …
Benar
\((4x^2\:-\:9)(4x^2\:-\:8x \:-\:21) > 0\)
\((2x + 3)(2x\:-\:3)(2x\:-\:7)(2x + 3) > 0\)
\((2x + 3)^2(2x\:-\:3)(2x\:-\:7) > 0\)
Pembuat-pembuat nol:
\(2x + 3 = 0 \rightarrow x = -\frac{3}{2}\)
\(2x\:-\:3 = 0 \rightarrow x = \frac{3}{2}\)
\(2x\:-\:7 = 0 \rightarrow x = \frac{7}{2}\)

Himpunan penyelesaian : \(\lbrace x | x < \frac{3}{2} \text{ atau } x > \frac{7}{2}, x \neq -\frac{3}{2}, x \in \text{R}\rbrace\)
Salah
\((4x^2\:-\:9)(4x^2\:-\:8x \:-\:21) > 0\)
\((2x + 3)(2x\:-\:3)(2x\:-\:7)(2x + 3) > 0\)
\((2x + 3)^2(2x\:-\:3)(2x\:-\:7) > 0\)
Pembuat-pembuat nol:
\(2x + 3 = 0 \rightarrow x = -\frac{3}{2}\)
\(2x\:-\:3 = 0 \rightarrow x = \frac{3}{2}\)
\(2x\:-\:7 = 0 \rightarrow x = \frac{7}{2}\)

Himpunan penyelesaian : \(\lbrace x | x < \frac{3}{2} \text{ atau } x > \frac{7}{2}, x \neq -\frac{3}{2}, x \in \text{R}\rbrace\)
-
Pertanyaan 2 dari 7
2. Pertanyaan
1 points\(\dfrac{(x^2\:-\:16)(x^2\:-\:2x\:-\:24)}{2x^2\:-\:9x\:-\:5}\) selalu bernilai negatif untuk …
Benar
\(\dfrac{(x + 4)(x\:-\:4)(x\:-\:6)(x + 4)}{(2x + 1)(x\:-\:5)} < 0\)
\(\dfrac{(x + 4)^2(x\:-\:4)(x\:-\:6)}{(2x + 1)(x\:-\:5)} < 0\)
Pembuat-pembuat nol:
\(x + 4 = 0 \rightarrow x = -4\)
\(x\:-\:4 =0 \rightarrow x = 4\)
\(x\:-\:6 = 0 \rightarrow x = 6\)
\(2x + 1 \neq 0 \rightarrow x \neq -\frac{1}{2}\)
\(x\:-\: 5 \neq 0 \rightarrow x \neq 5\)

Himpunan penyelesaian : \(\lbrace x | -\frac{1}{2} < x < 4, \text{ atau } 5 < x < 6,\: x \in \text{R}\rbrace\)
Salah
\(\dfrac{(x + 4)(x\:-\:4)(x\:-\:6)(x + 4)}{(2x + 1)(x\:-\:5)} < 0\)
\(\dfrac{(x + 4)^2(x\:-\:4)(x\:-\:6)}{(2x + 1)(x\:-\:5)} < 0\)
Pembuat-pembuat nol:
\(x + 4 = 0 \rightarrow x = -4\)
\(x\:-\:4 =0 \rightarrow x = 4\)
\(x\:-\:6 = 0 \rightarrow x = 6\)
\(2x + 1 \neq 0 \rightarrow x \neq -\frac{1}{2}\)
\(x\:-\: 5 \neq 0 \rightarrow x \neq 5\)

Himpunan penyelesaian : \(\lbrace x | -\frac{1}{2} < x < 4, \text{ atau } 5 < x < 6,\: x \in \text{R}\rbrace\)
-
Pertanyaan 3 dari 7
3. Pertanyaan
1 pointsBanyaknya bilangan bulat positif yang memenuhi pertidaksamaan \((x\:-\:\frac{6}{x})^2\:-\:6(x\:-\:\frac{6}{x}) + 5 \leq 0\) adalah …
Benar
\(\text{Misal } x\:-\:\frac{6}{x} = p\)
\(p^2 \:-\:6p + 5 \leq 0\)
\((p\:-\:5)(p\:-\:1) \leq 0\)

\(1 \leq p \leq 5\)
\(1 \leq x\:-\:\frac{6}{x} \leq 5\)
\(x\:-\:\frac{6}{x} \geq 1 \text{ dan } x\:-\:\frac{6}{x} \leq 5\)
\(x\:-\:\frac{6}{x}\:-\: 1\geq 0 \text{ dan } x\:-\:\frac{6}{x}\:-\:5 \leq 0\)
\(\dfrac{x^2\:-\:x\:-\:6}{x} \geq 0\)
dan
\(\dfrac{x^2\:-\:x\:-\:6}{x} \leq 0\)
\(\dfrac{(x\:-\:3)(x + 2)}{x} \geq 0\)
dan
\(\dfrac{(x\:-\:6)(x + 1)}{x} \leq 0\)
Penyelesaian kiri:

Penyelesaian kanan:

Irisan dari penyelesaian kiri dan penyelesaian kanan adalah :
\(\lbrace -2\leq x \leq -1 \text{ atau } 3 \leq x \leq 6, \: x \in \text{R} \rbrace\)
Bilangan bulat positif yang memenuhi adalah 3, 4, 5, dan 6 ada sebanyak 4 bilangan.
Salah
\(\text{Misal } x\:-\:\frac{6}{x} = p\)
\(p^2 \:-\:6p + 5 \leq 0\)
\((p\:-\:5)(p\:-\:1) \leq 0\)

\(1 \leq p \leq 5\)
\(1 \leq x\:-\:\frac{6}{x} \leq 5\)
\(x\:-\:\frac{6}{x} \geq 1 \text{ dan } x\:-\:\frac{6}{x} \leq 5\)
\(x\:-\:\frac{6}{x}\:-\: 1\geq 0 \text{ dan } x\:-\:\frac{6}{x}\:-\:5 \leq 0\)
\(\dfrac{x^2\:-\:x\:-\:6}{x} \geq 0\)
dan
\(\dfrac{x^2\:-\:x\:-\:6}{x} \leq 0\)
\(\dfrac{(x\:-\:3)(x + 2)}{x} \geq 0\)
dan
\(\dfrac{(x\:-\:6)(x + 1)}{x} \leq 0\)
Penyelesaian kiri:

Penyelesaian kanan:

Irisan dari penyelesaian kiri dan penyelesaian kanan adalah :
\(\lbrace -2\leq x \leq -1 \text{ atau } 3 \leq x \leq 6, \: x \in \text{R} \rbrace\)
Bilangan bulat positif yang memenuhi adalah 3, 4, 5, dan 6 ada sebanyak 4 bilangan.
-
Pertanyaan 4 dari 7
4. Pertanyaan
1 pointsHimpunan penyelesaian pertidaksamaan \(x^2(x\:-\:3)\:-\:9(x\:-\:3) < 0\) adalah …
Benar
\(x^2(x\:-\:3)\:-\:9(x\:-\:3) < 0\)
\((x\:-\:3)(x^2\:-\:9) < 0\)
\((x\:-\:3)(x + 3)(x\:-\:3) < 0\)
\((x\:-\:3)^2(x + 3) < 0\)
Pembuat-pembuat nol:
\(x\:-\:3 = 0 \rightarrow x = 3\)
\(x + 3 = 0 \rightarrow x = -3\)
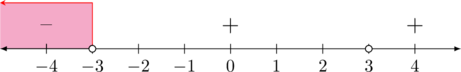
HP = \(\lbrace x| x < -3, \:x\in \text{R} \rbrace\)
Salah
\(x^2(x\:-\:3)\:-\:9(x\:-\:3) < 0\)
\((x\:-\:3)(x^2\:-\:9) < 0\)
\((x\:-\:3)(x + 3)(x\:-\:3) < 0\)
\((x\:-\:3)^2(x + 3) < 0\)
Pembuat-pembuat nol:
\(x\:-\:3 = 0 \rightarrow x = 3\)
\(x + 3 = 0 \rightarrow x = -3\)
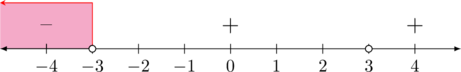
HP = \(\lbrace x| x < -3, \:x\in \text{R} \rbrace\)
-
Pertanyaan 5 dari 7
5. Pertanyaan
1 pointsHimpunan penyelesaian pertidaksamaan \(\dfrac{x+2}{x\:-\:1} \leq \dfrac{x\:-\:1}{x + 2}\) adalah …
Benar
\(\dfrac{x+2}{x\:-\:1} \leq \dfrac{x\:-\:1}{x + 2}\)
\(\dfrac{x+2}{x\:-\:1} \:-\: \dfrac{x\:-\:1}{x + 2} \leq 0\)
\(\dfrac{(x + 2)(x + 2)\:-\:(x\:-\:1)(x\:-\:1)}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{x^2 + 4x + 4\:-\:(x^2\:-\:2x + 1)}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{x^2 + 4x + 4\:-\:x^2 + 2x \:-\:1}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{6x + 3}{(x\:-\:1)(x + 2)}\leq 0\)
Pembuat-pembuat nol:
\( 6x + 3 = 0 \rightarrow x = -\frac{1}{2}\)
\(x\:-\:1 \neq 0 \rightarrow x \neq 1\)
\(x + 2 \neq 0 \rightarrow x \neq -2\)
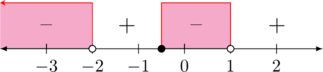
HP : \(\lbrace x | x < -2 , \text{ atau } -\frac{1}{2} \leq x < 1, \: x\in \text{R}\rbrace\)
Salah
\(\dfrac{x+2}{x\:-\:1} \leq \dfrac{x\:-\:1}{x + 2}\)
\(\dfrac{x+2}{x\:-\:1} \:-\: \dfrac{x\:-\:1}{x + 2} \leq 0\)
\(\dfrac{(x + 2)(x + 2)\:-\:(x\:-\:1)(x\:-\:1)}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{x^2 + 4x + 4\:-\:(x^2\:-\:2x + 1)}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{x^2 + 4x + 4\:-\:x^2 + 2x \:-\:1}{(x\:-\:1)(x + 2)}\leq 0\)
\(\dfrac{6x + 3}{(x\:-\:1)(x + 2)}\leq 0\)
Pembuat-pembuat nol:
\( 6x + 3 = 0 \rightarrow x = -\frac{1}{2}\)
\(x\:-\:1 \neq 0 \rightarrow x \neq 1\)
\(x + 2 \neq 0 \rightarrow x \neq -2\)

HP : \(\lbrace x | x < -2 , \text{ atau } -\frac{1}{2} \leq x < 1, \: x\in \text{R}\rbrace\)
-
Pertanyaan 6 dari 7
6. Pertanyaan
1 pointsKurva \(y = \dfrac{2x + 6}{x + 1}\) berada di atas garis \(y = -2\) pada interval …
Benar
\(\dfrac{2x + 6}{x + 1} > -2\)
\(\dfrac{2x + 6}{x + 1} + 2 > 0\)
\(\dfrac{2x + 6 + 2(x + 1)}{x + 1} > 0\)
\(\dfrac{4x + 8}{x + 1} > 0\)
Pembuat-pembuat nol:
\(4x + 8 = 0 \rightarrow x = -2\)
\(x + 1 = 0 \rightarrow x = -1\)
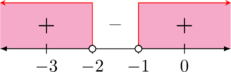
HP: \(\lbrace x < -2 \text{ atau } x > -1, \: x\in \text{R}\rbrace\)
Salah
\(\dfrac{2x + 6}{x + 1} > -2\)
\(\dfrac{2x + 6}{x + 1} + 2 > 0\)
\(\dfrac{2x + 6 + 2(x + 1)}{x + 1} > 0\)
\(\dfrac{4x + 8}{x + 1} > 0\)
Pembuat-pembuat nol:
\(4x + 8 = 0 \rightarrow x = -2\)
\(x + 1 = 0 \rightarrow x = -1\)

HP: \(\lbrace x < -2 \text{ atau } x > -1, \: x\in \text{R}\rbrace\)
-
Pertanyaan 7 dari 7
7. Pertanyaan
1 pointsBanyaknya bilangan bulat yang lebih dari 1 yang memenuhi pertidaksamaan \(x + 4 \leq \dfrac{2x + 16}{x \:-\:1}\) adalah …
Benar
\(x + 4 \leq \dfrac{2x + 16}{x \:-\:1}\)
\(\dfrac{x + 4}{1}\:-\:\dfrac{(2x + 16)}{x \:-\:1} \leq 0\)
\(\dfrac{(x + 4)(x\:-\:1)\:-\:(2x + 16)}{x\:-\:1} \leq 0\)
\(\dfrac{x^2 + x \:-\:20}{x\:-\:1} \leq 0\)
\(\dfrac{(x + 5)(x\:-\:4)}{x\:-\:1} \leq 0\)

HP = \(\lbrace x | x \leq -5 \text{ atau } 1 < x \leq 4 \rbrace\)
Bilangan bulat yang lebih dari 1 adalah 2, 3, dan 4 (ada 3 bilangan)
Salah
\(x + 4 \leq \dfrac{2x + 16}{x \:-\:1}\)
\(\dfrac{x + 4}{1}\:-\:\dfrac{(2x + 16)}{x \:-\:1} \leq 0\)
\(\dfrac{(x + 4)(x\:-\:1)\:-\:(2x + 16)}{x\:-\:1} \leq 0\)
\(\dfrac{x^2 + x \:-\:20}{x\:-\:1} \leq 0\)
\(\dfrac{(x + 5)(x\:-\:4)}{x\:-\:1} \leq 0\)

HP = \(\lbrace x | x \leq -5 \text{ atau } 1 < x \leq 4 \rbrace\)
Bilangan bulat yang lebih dari 1 adalah 2, 3, dan 4 (ada 3 bilangan)
