(x + a) adalah salah satu faktor dari suku banyak f(x), jika dan hanya jika f(−a) = 0
Contoh 1:
Jika \(x\:-\:4\) adalah salah satu faktor dari suku banyak \(f(x) = x^4\:-\:px^3\:-\:2x^2 + 8x\), tentukan nilai \(p\).
Penyelesaian:
Karena \(x\:-\:4\) adalah faktor dari \(f(x)\) maka \(f(4) = 0\)
\(f(4) = (4)^4\:-\:p(4)^3\:-\:2(4)^2 + 8(4)\)
\(0 = 256\:-\:64p\:-\:32 + 32\)
\(0 = 256\:-\:64p\)
\(64p = 256\)
\(p = 256 \div 64\)
\(p = 4\)
Jadi, nilai \(p\) adalah 4
Contoh 2:
Jika \(x + p\) adalah faktor dari \(g(x) = x^2 + 4x \:-\:5\), tentukan nilai \(p\).
Penyelesaian:
Karena \(x + p\) adalah faktor dari \(g(x)\) maka \(g(-p) = 0\)
\(g(-p) = (-p)^2 + 4(-p)\:-\:5\)
\(0 =p^2\:-\:4p\:-\:5\)
\(0 =(p\:-\:5)(p + 1)\)
\(p\:-\:5 = 0 \rightarrow p = 5\)
\(p + 1 = 0 \rightarrow p = -1\)
Jadi, nilai \(p\) adalah 5 atau −1
LATIHAN SOAL
Soal 01
Jika \((x + 1)\) dan \((x \:-\:2)\) adalah faktor dari polinomial \(p(x) = 2x^4 \:-\:5x^3 + (2a\:-\:4)x^2 + (-4\:-\:6b)x + 4\), maka faktor linear yang lain adalah…
(A) \((2x + 1)(x\:-\: 2)\)
(B) \((2x \:-\: 1)(x\:-\: 2)\)
(C) \((2x + 1)(x\:-\: 3)\)
(D) \((3x + 1)(x\:-\: 2)\)
(E) \((2x + 3)(x+ 5)\)
Answer: A
Dengan menggunakan teorema faktor \(p(-1) = 0\) dan \(p(2) = 0\)
\(p(-1) = 2(-1)^4\:-\:5(-1)^3 + (2a\:-\:4)(-1)^2 + (-4\:-\:6b)(-1) + 4 = 0\)
\(2 + 5 + 2a\:-\:4 + 4 + 6b + 4 = 0\)
\(11 + 2a + 6b = 0\)
\(2a + 6b = -11 \dotso \color{red} (1)\)
\(p(2) = 2(2)^4\:-\:5(2)^3 + (2a\:-\:4)(2)^2 + (-4\:-\:6b)(2) + 4 = 0\)
\(32 \:-\:40 + 8a \:-\: 16\:-\:8 \:-\:12b + 4 = 0\)
\(-28 + 8a \:-\:12b = 0\)
\(-7 + 2a\:-\:3b = 0\)
\(2a\:-\:3b = 7 \dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) sehingga didapatkan nilai \(a = \dfrac{1}{2}\) dan \(b = -2\)
\(p(x) = 2x^4 \:-\:5x^3 \:-\:3x^2 + 8x + 4\)
\(p(x)\) dibagi dengan \((x+1)(x\:-\:2) = x^2\:-\:x\:-\:2\)
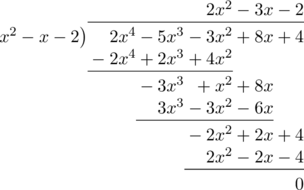
Faktor yang lain berasal dari hasil baginya yaitu \(2x^2 \:-\:3x \:-\:2\)
\(2x^2 \:-\:3x \:-\:2 = (2x + 1)(x\:-\: 2)\)
Soal 02
Jika \(2x\:-\:3y + 2\) merupakan faktor \(ax^2 + bxy + cy^2 \:-\:4x + 19y \:-\:10\), maka nilai \(a + b \:-\:2c = \dotso\)
(A) 21
(B) 22
(C) 23
(D) 24
(E) 28
Answer: E
\(2x\:-\:3y + 2 \rightarrow x = \frac{3}{2}y\:-\:1\)
\(p(x) = ax^2 + bxy + cy^2 \:-\:4x + 19y \:-\:10\)
\(p(x) = ax^2 + (by\:-\:4)x + cy^2 + 19y\:-\:10\)
\(p(\frac{3}{2}y\:-\:1) =0\)
\(a(\frac{3}{2}y\:-\:1)^2 + (by\:-\:4)(\frac{3}{2}y\:-\:1)+ cy^2 + 19y\:-\:10 = 0\)
\(a(\frac{9}{4}y^2 \:-\:3y + 1) + \frac{3}{2}by^2\:-\:by\:-\:6y + 4 + cy^2 + 19y\:-\:10 = 0\)
\((\frac{9}{4}a + \frac{3}{2}b + c)y^2 + (-3a \:-\:b + 19)y + (a\:-\:6) = 0\)
Koefisien dari masing-masing suku harus nol
\(\frac{9}{6}a + \frac{3}{2}b + c = 0\dotso \color{red} (1)\)
\(-3a\:-\:b + 19 = 0\dotso \color{red} (2)\)
\(a\:-\:6 = 0\dotso \color{red} (3)\)
\(a\:-\:6 = 0 \rightarrow a = 6\)
\(-3(6)\:-\:b + 19 = 0\)
\(-18\:-\:b + 19 = 0\)
\(b = 1\)
\(\frac{9}{6}(6) + \frac{3}{2}(1) + c = 0\)
\(9 + \frac{3}{2} + c = 0\)
\(c = -\frac{21}{2}\)
\(a + b \:-\:2c = 6 + 1 \:-\:2(-\frac{21}{2})\)
\(a + b \:-\:2c = 28\)
