Ciri-Ciri Kubus
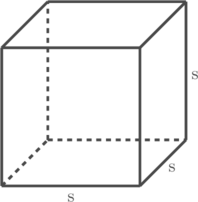
Kubus (Cube) adalah bangun ruang 3 dimensi dengan ciri-ciri:
- Memiliki 6 buah sisi yang sama dan berbentuk persegi
- Memiliki 12 rusuk yang sama panjang
- Memiliki 8 buah titik sudut
Jaring-Jaring Kubus
Kubus dapat dibuat dengan berbagai macam jaring-jaring.
Contoh jaring-jaring kubus:
Volume Kubus
\(\textbf{Volume Kubus} = \textbf{s}^3\)
\(\text {s} = \text{panjang rusuk (panjang sisi)}\)
Luas Permukaan Kubus
Sisi sebuah kubus berbentuk persegi. Karena kubus terdiri dari 6 buah sisi yang berbentuk persegi, maka luas permukaan kubus adalah 6 kali luas sisi kubus.
\(\textbf{Luas Permukaan Kubus} = 6\times\textbf{s}^2\)
🧩 CONTOH SOAL
Q1
Sebuah kotak mainan berbentuk kubus dengan panjang sisi 30 cm. Tentukan volume dan luas permukaan kubus tersebut.
Panjang sisi/rusuk kubus = 30 cm
Volume kubus = \(\text{s}^3\)
Volume kubus = \(\text{(30 cm)}^3\)
Volume kubus = \(\text{30 cm}\times \text{30 cm} \times \text{30 cm}\)
Volume kubus = \(27.000 \text{ cm}^3\)
Luas permukaan kubus = \(6\times \text{s}^2\)
Luas permukaan kubus = \(6\times \text{(30 cm)}^2\)
Luas permukaan kubus = \(6\times \text{30 cm}\times \text{30 cm}\)
Luas permukaan kubus = \(6\times 900 \text{ cm}^2\)
Luas permukaan kubus = \(5.400 \text{ cm}^2\)
Q2
Sebuah kubus memiliki luas alas sebesar 64 cm² dan terisi air setinggi 3 cm. Tentukan volume air di dalam kubus tersebut.
Luas alas \((\text{s}^2)\) = 64 cm²
Tinggi air = 3 cm
Volume air = \(\text{luas alas kubus} \times \text{ketinggian air}\)
Volume air = \(64 \text{ cm}^2 \times 3 \text{ cm}\)
Volume air = \(192 \text{ cm}^3\)
Q3
Sebuah tempat penampungan air berbentuk kubus memiliki panjang sisi 60 cm. Jika setengah bagian kubus tersebut terisi oleh air, maka tentukan volume air di dalam kubus.
Karena kubus hanya terisi air setengah bagian, maka volume air di dalam kubus sama dengan setengah volume kubus.
Volume air = \(\frac{1}{2}\times \text{volume kubus}\)
Volume air = \(\frac{1}{2}\times \text{s}^3\)
Volume air = \(\frac{1}{2}\times \text{(60 cm)}^3\)
Volume air = \(\frac{1}{2}\times \text{60 cm}\times \text{60 cm} \times \text{60 cm}\)
Volume air = \(\frac{1}{2}\times 216.000\text{ cm}^3\)
Volume air = \(108.000\text{ cm}^3\)
Q4
Sebuah tempat penampungan air berbentuk kubus memiliki panjang sisi 10 cm. Jika seperempat bagian kubus tersebut sudah terisi oleh air, maka tentukan volume air yang harus ditambahkan agar kubus terisi air sampai penuh.
Kubus yang terisi air penuh kita anggap 1 bagian. Karena mula-mula kubus sudah terisi air ¼ bagian, maka volume air yang harus ditambahkan adalah \(1\:-\:\frac{1}{4} = \frac{3}{4}\) bagian.
Volume air yang ditambahkan = \(\frac{3}{4}\times \text{volume kubus}\)
Volume air yang ditambahkan = \(\frac{3}{4}\times \text{s}^3\)
Volume air yang ditambahkan = \(\frac{3}{4}\times \text{(10 cm)}^3\)
Volume air yang ditambahkan = \(\frac{3}{4}\times 1.000 \text{ cm}^3\)
Volume air yang ditambahkan = \(\frac{3}{\cancel{4}}\times \cancelto{250}{1.000} \text{ cm}^3\)
Volume air yang ditambahkan = \(750\text{ cm}^3\)
Q5
Dodi memiliki 4 buah dadu yang sama berbentuk kubus dengan ukuran sisi 5 cm. Jika permukaan keempat dadu tersebut akan diwarnai seluruhnya oleh Dodi, maka tentukan total luas permukaan keempat dadu yang diwarnai.
Total luas pemukaan 4 buah dadu yang diwarnai = \(4\times 6 \times \text{ s }^2\)
Total luas pemukaan 4 buah dadu yang diwarnai = \(4\times 6 \times \text{ (5 cm)}^2\)
Total luas pemukaan 4 buah dadu yang diwarnai = \(24 \times \text{ 25 cm}^2\)
Total luas pemukaan 4 buah dadu yang diwarnai = \(600\text{ cm}^2\)
Q6
Sebuah kubus memiliki volume 4.913 cm³. Tentukan panjang sisi kubus tersebut.
Panjang sisi kubus = \(\sqrt[3] {\text{volume kubus}}\)
Panjang sisi kubus = \(\sqrt[3] {\text{4.913 cm³}}\)
Panjang sisi kubus = \(\sqrt[3] {17 \text{ cm}\times 17 \text{ cm} \times 17 \text{ cm}}\)
Panjang sisi kubus = \(17 \text{ cm}\)
Q7
Terdapat tumpukan kubus-kubus kecil yang identik seperti pada gambar di bawah ini.
Setiap kubus memiliki ukuran sisi 2 cm.
Tentukan Benar atau Salah setiap pernyataan berikut ini.
(1) Jumlah kubus-kubus kecil pada tumpukan ada 5 buah.
(2) Volume tumpukan kubus-kubus kecil \(60 \text{ cm}^3\)
Terdapat 5 kubus kecil yang ditumpuk. (Pernyataan 1 benar)
Volume tumpukan = 5 × volume kubus kecil
Volume tumpukan = \(5 \times 2^3\)
Volume tumpukan = \(5 \times 8 = 40 \text{ cm}^3\)
(Pernyataan 2 salah)
