Soal 1
Perhatikan gambar berikut:
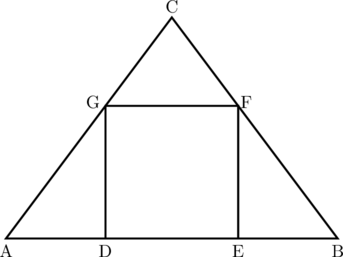
Segitiga ABC adalah segitiga sama kaki. Panjang AC sama dengan BC dan panjang AB = 40 cm. DEFG adalah sebuah persegi yang memiliki ukuran sisi 16 cm. Luas segitiga ABC adalah …
(A) \(\dfrac{1400}{3}\text{ cm}^2\)
(B) \(\dfrac{1500}{3}\text{ cm}^2\)
(C) \(\dfrac{1600}{3}\text{ cm}^2\)
(D) \(\dfrac{1700}{3}\text{ cm}^2\)
Jawaban: C
Langkah 1: Mencari tinggi segitiga ABC
Buat garis bantuan CH.
Panjang DH = HE = 8 cm (karena titik H berada di tengah DE)
Panjang AD sama dengan panjang EB = 12 cm
Hitungan:
AD = (AB − DE) ÷ 2
AD = (40 − 16) ÷ 2
AD = 24 ÷ 2 = 12 cm

Perhatikan segitiga ADG dan segitiga AHC
\(\color{blue}\triangle \text{ADG} \text{ sebangun dengan } \triangle \text{AHC}\)
Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama

\(\dfrac{\text{AD}}{\text{AH}} = \dfrac{\text{DG}}{\text{HC}}\)
\(\dfrac{12}{12 + 8} = \dfrac{16}{\text{HC}}\)
\(\dfrac{12}{20} = \dfrac{16}{\text{HC}}\)
\(\dfrac{3}{5} = \dfrac{16}{\text{HC}}\:\:\:\:\color{blue}\text{kali silang}\)
\(3\times \text{HC} = 16 \times 5\)
\(3\times \text{HC} = 80\)
\(\text{HC} = \dfrac{80}{3} \text{ cm}\)
Jadi tinggi segitiga ABC adalah \(\dfrac{80}{3} \text{ cm}\)
Langkah 2: Menghitung luas segitiga ABC
Luas segitiga ABC = \(\dfrac{1}{2} \times \text{AB} \times \text{HC}\)
Luas segitiga ABC = \(\dfrac{1}{2} \times 40 \text{ cm} \times \dfrac{80}{3} \text{ cm}\)
Luas segitiga ABC = \(\dfrac{1}{\cancel{2}} \times \cancelto{20}{40} \text{ cm} \times \dfrac{80}{3} \text{ cm}\)
Luas segitiga ABC = \(\dfrac{1600}{3}\text{ cm}^2\)
Soal 2
Perhatikan gambar berikut:

ABCD adalah sebuah persegi panjang dengan luas 66 cm² dan memiliki panjang AB = 11 cm. AEFD, EGHI, dan IJCF berbentuk persegi, sedangkan GBJH berbentuk persegi panjang. Luas persegi panjang GBJH adalah …
(A) 4 cm²
(B) 6 cm²
(C) 8 cm²
(D) 10 cm²
Jawaban: A
Langkah 1: Mencari lebar persegi panjang ABCD
Luas persegi panjang = panjang × lebar
66 cm² = 11 cm × lebar
lebar = 66 cm² ÷ 11 cm = 6 cm
Langkah 2: Menentukan ukuran setiap bangun datar yang terbentuk

Langkah 3: Menentukan Luas Persegi Panjang GBJH
Luas persegi panjang GBJH = GB × BJ
Luas persegi panjang GBJH = 4 cm × 1 cm
Luas persegi panjang GBJH = 4 cm²
Soal 3
Sebuah trapezium sama kaki ABCD, memiliki koordinat titik A\((-4, -3)\), B\((4, -3)\), C\((2, 3)\), dan D\((-2, 3)\). Luas trapezium sama kaki ABCD tersebut adalah … satuan luas
(A) 26
(B) 30
(C) 32
(D) 36
Jawaban: E
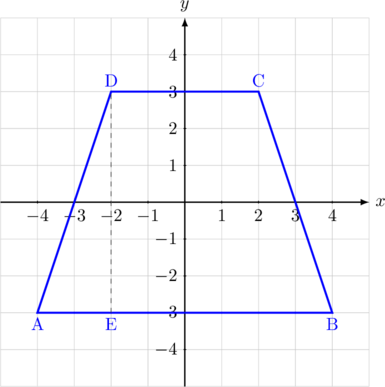
Luas trapesium = [jumlah sisi sejajar × tinggi] ÷ 2
Luas trapesium = [(AB + DC) × DE] ÷ 2
Luas trapesium = [(8 + 4) × 6] ÷ 2
Luas trapesium = [12 × 6] ÷ 2
Luas trapesium = 72 ÷ 2
Luas trapesium sama kaki ABCD = 36 satuan luas
Soal 4
Sepotong besi dengan panjang 25 cm dipanaskan sehingga panjangnya bertambah 8%. Sesudah pemanasan tersebut, besi kemudian didinginkan sehingga panjangnya menyusut sebesar 8%. Panjang besi sekarang adalah …
(A) 24,84 cm
(B) 25 cm
(C) 25,24 cm
(D) 27 cm
Jawaban: A
Langkah 1: Menentukan panjang besi setelah dipanaskan
Pertambahan panjang besi = 8% × 25 cm
Pertambahan panjang besi = \(\dfrac{8}{100}\) × 25 cm
Pertambahan panjang besi = \(\dfrac{2}{25}\) × 25 cm
Pertambahan panjang besi = 2 cm
Panjang besi setelah dipanaskan adalah 25 cm + 2 cm = 27 cm
Langkah 2: Menentukan panjang besi setelah didinginkan
Penyusutan panjang besi = 8% × 27 cm
Penyusutan panjang besi = \(\dfrac{8}{100}\) × 27 cm
Penyusutan panjang besi = \(\dfrac{216}{100}\) cm
Penyusutan panjang besi = 2,16 cm
Panjang besi setelah didinginkan adalah 27 cm − 2,16 cm = 24,84 cm
Soal 5
Perhatikan gambar berikut!
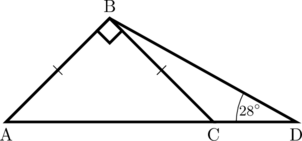
Segitiga ABC adalah segitiga siku-siku sama kaki. Jika besar sudut BDC = 28°, maka besar sudut DBC adalah …
(A) 20°
(B) 18°
(C) 17°
(D) 12°
Jawaban: C
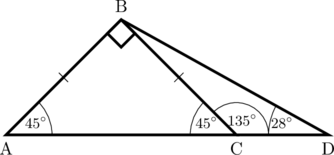
Karena \(\triangle \text{ABC}\) adalah segitiga siku-siku sama kaki, maka besar
\(\angle \text{BAC} = \angle \text{BCA} = 45^{\circ}\).
Selanjutnya, perhatikan segitiga BCD
Karena \(\angle \text{ACD}\) adalah sudut lurus (besarnya 180°), maka
Besar \(\angle \text{BCD} = 180^{\circ}\:-\:\angle \text{BCA}\)
Besar \(\angle \text{BCD} = 180^{\circ}\:-\:45^{\circ}\)
Besar \(\angle \text{BCD} = 135^{\circ}\)
Jumlah setiap sudut dalam segitiga adalah 180°
Besar \(\angle \text{DBC} = 180^{\circ}\:-\:28^{\circ}\:-\:135^{\circ}\)
Besar \(\angle \text{DBC} = 17^{\circ}\)
Soal 6
Tiga buah mesin pompa air A, B, dan C berbahan bakar bensin mampu beroperasi terus-menerus, kecuali saat pengisian bahan bakar. Mesin-mesin tersebut digunakan untuk menyedot air dari sungai untuk dialirkan ke kolam-kolam budidaya ikan air tawar milik petani. Mesin A mengisi bahan bakar setiap 3 jam sekali, mesin B mengisi bahan bakar setiap 4 jam sekali, dan mesin C mengisi bahan bakar setiap 5 jam sekali. Setiap pengisian bahan bakar mesin berhenti beroperasi selama 1 jam. Jika mesin-mesin tersebut secara bersama-sama beroperasi mulai hari Sabtu pukul 06:00, maka ketiga mesin akan mengisi bahan bakar bensin secara bersama-sama untuk pertama kalinya pada …
(A) Senin pukul 06:00
(B) Senin pukul 12:00
(C) Senin pukul 15:00
(D) Senin pukul 18:00
Jawaban: D
Berikut ini adalah waktu untuk pengisian bahan bakar setiap mesin selanjutnya:
Mesin A = 3 jam + 1 jam = 4 jam
Mesin B = 4 jam + 1 jam = 5 jam
Mesin C = 5 jam + 1 jam = 6 jam
Semuanya ditambah 1 jam karena setelah pengisian bahan bakar mesin tidak dioperasikan selama 1 jam.
Selanjutnya, mencari KPK dari 4, 5, dan 6
Faktorisasi prima dari 4 adalah 2²
Faktorisasi prima dari 5 adalah 5
Faktorisasi prima dari 6 adalah 2 × 3
KPK dari 4, 5, dan 6 adalah 2² × 3 × 5 = 60 jam
Ketiga mesin akan mengisi bahan bakar bensin secara bersama-sama untuk pertama kalinya 60 jam mendatang dihitung dari pukul 06:00 hari Sabtu.
Catatan: 1 hari = 24 jam
Sabtu pukul 06:00 sampai Minggu pukul 06:00 = 24 jam
Minggu pukul 06:00 sampai Senin pukul 06:00 = 24 jam
Senin pukul 06:00 – 18:00 = 12 jam
Jadi, ketiga mesin akan mengisi bahan bakar bensin secara bersama-sama untuk pertama kalinya pada hari Senin pukul 18:00
Soal 7
\(1\:-\:2 + 3 \:-\:4 + 5 \:-\:6 + \dotso + 2001\:-\:2002 + 2003 = \dotso\)
(A) 1001
(B) 1002
(C) 1003
(D) 1004
Jawaban: B
![]()
\(1001 \times (-1) + 2003\)
\(-1001 + 2003\)
\(2003 \:-\:1001\)
\(1002\)
Soal 8
Sebuah bilangan terdiri dari 3 digit (angka) tersusun dari angka-angka 5, 7, 2. Jika tidak ada angka yang berulang, maka jumlah bilangan terbesar dan terkecil yang terbentuk adalah …
(A) 1007
(B) 1008
(C) 1009
(D) 1010
Jawaban: C
Dari angka-angka 5, 7, 2, bilangan terbesar yang dapat dibentuk adalah 752 dan bilangan terkecil yang dapat dibentuk adalah 257.
752 + 257 = 1009
Soal 9
Nilai rata-rata ulangan matematika dari 39 orang siswa di kelas 5 adalah 80. Jika ada seorang siswa yang mengikuti ulangan susulan matematika, dan nilainya digabung dengan jumlah nilai 39 siswa lainnya, maka nilai rata-rata ulangan matematika di kelas 5 menjadi 80,5. Nilai ulangan matematika siswa yang mengikuti susulan tersebut adalah …
(A) 80
(B) 85
(C) 90
(D) 100
Jawaban: D
Langkah 1: Menentukan jumlah nilai ulangan matematika 39 orang siswa
\(\text{Rata-rata} = \dfrac{\text{jumlah nilai}}{\text{banyak siswa}}\)
\(80 = \dfrac{\text{jumlah nilai dari 39 orang siswa}}{39}\)
\(\text{Jumlah nilai 39 orang siswa} = 80 \times 39 = 3.120\)
Misal nilai seorang siswa yang mengikuti susulan adalah \(x\)
Setelah nilainya digabung dengan nilai 39 siswa yang lain, nilai rata-rata kelas menjadi 80,5
\(\text{Rata-rata baru} = \dfrac{\text{jumlah nilai}}{\text{banyak siswa}}\)
\(80,5 = \dfrac{\text{jumlah nilai dari 39 orang siswa} + x}{39 + 1}\)
\(80,5 = \dfrac{3.120 + x}{39 + 1}\)
\(80,5 = \dfrac{3.120 + x}{40}\)
\(80,5 \times 40 = 3.120 + x\)
\(3.220 = 3.120 + x\)
\(3.220\:-\:3.120 = x\)
\(x = 100\)
Jadi, nilai siswa yang mengikuti ulangan susulan adalah 100
Soal 10
Pak Rudi membeli ikan lele hidup sebanyak 100 kg dari peternak lele untuk dijual kembali di pasar. Harga 1 kg ikan lele dari peternak adalah Rp15.000,00. Dalam perjalanan ke pasar, terdapat 2 kg ikan lele yang mati. Jika Pak Rudi hanya menjual kembali ikan lele yang hidup dengan harga Rp18.000,00 per kg, maka keuntungan yang didapat oleh Pak Rudi adalah …
(A) Rp264.000,00
(B) Rp268.000,00
(C) Rp290.000,00
(D) Rp300.000,00
Jawaban: A
Harga beli ikan lele 100 kg = Rp15.000,00 × 100 = Rp1.500.000,00
Banyaknya ikan lele yang dijual kembali (yang masih hidup) = 100 kg − 2 kg = 98 kg
Harga jual ikan lele 98 kg = Rp18.000,00 × 98 = Rp1.764.000,00
Keuntungan = harga jual − harga beli
Keuntungan = Rp1.764.000,00 − Rp1.500.000,00
Keuntungan = Rp264.000,00
Jadi, keuntungan yang didapat oleh Pak Rudi adalah Rp264.000,00
