Halo, teman-teman! Pernahkah kalian melihat bentuk lintasan bola saat dilempar ke udara? Atau mungkin bentuk jembatan melengkung yang indah? Nah, ternyata, bentuk-bentuk ini bisa dijelaskan dengan fungsi kuadrat!
Fungsi kuadrat adalah salah satu fungsi yang berbentuk kurva parabola. Parabola bisa melengkung ke atas seperti senyum atau ke bawah seperti sedih.
Di sini, kita akan belajar bagaimana cara menggambar grafik fungsi kuadrat dengan mudah dan menyenangkan! Kita akan menemukan titik puncak parabola, titik potong kurva terhadap sumbu-x dan juga sumbu-y. Jangan khawatir, kita akan belajar langkah demi langkah!
Siap menggambar parabola? Yuk, kita mulai petualangan menggambar fungsi kuadrat!
Fungsi kuadrat memiliki persamaan umum:
$$\bbox[yellow, 5px, border: 2px solid red] {f(x) = ax^2 + bx + c}$$
dengan \(a \neq 0\)
Menggambar fungsi kuadrat dengan melengkapi tabel
Soal 1
Gambarkan grafik fungsi \(f(x) = x^2\)
| \(x\) | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| \(y = f(x)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Cara melakukan perhitungan:
Untuk \(x = -3\)
\(f(-3) = (-3)^2 = \color{blue} 9\)
Tandai titik-titik (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9) pada diagram cartesius kemudian hubungkan semua titik tersebut sehingga diperoleh gambar grafik \(f(x) = x^2\) seperti di bawah ini.
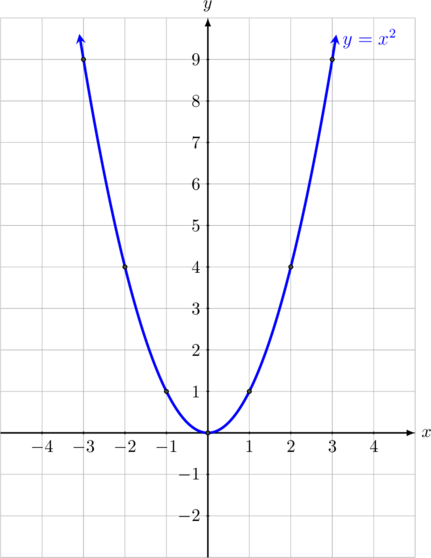
Berikut ini adalah karakteristik grafik \(f(x) = x^2\)
- berbentuk parabola yang terbuka ke atas, karena nilai \(a > 0\)
- memiliki titik balik minimum di \((0, 0)\)
- menyinggung sumbu \(x\) di titik \((0, 0)\)
Soal 2
Gambarkan grafik fungsi \(f(x) = x^2 \:- \: 2x\: -\: 3\)
| \(x\) | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| \(y = f(x)\) | 12 | 5 | 0 | −3 | −4 | −3 | 0 |
Cara melakukan perhitungan:
Untuk \(x = -3\)
\(f(-3) = (-3)^2\: -\:2(-3)\: -|; 3\)
\( 9 + 6 \:- \:3 = \color{blue} 12\)
Tandai titik-titik (-3, 12), (-2, 5), (-1, 0), (0, -3), (1, -4), (2, -3), (3,0) pada diagram cartesius kemudian hubungkan semua titik tersebut sehingga diperoleh gambar grafik \(f(x) = x^2 \:- \:2x\: -\: 3\) seperti di bawah ini.
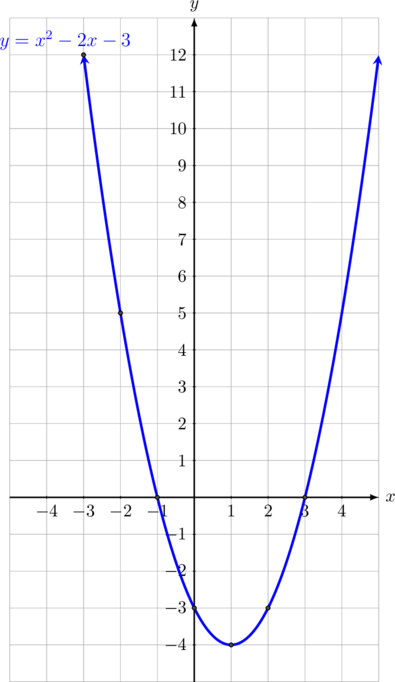
Berikut ini adalah karakteristik grafik \(f(x) = x^2\: -\: 2x\: -\: 3\)
- berbentuk parabola yang terbuka ke atas, karena nilai \(a > 0\)
- memiliki titik balik minimum di \((1,-4)\)
- memotong sumbu \(x\) di titik \((-1, 0) \text{ dan } (3, 0)\)
- memotong sumbu \(y\) di titik \((0,-3)\)
Soal 3
Gambarkan grafik fungsi \(f(x) = -2x^2\: -\: 4x +6\)
| \(x\) | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| \(y = f(x)\) | 0 | 6 | 8 | 6 | 0 | −10 | −24 |
Cara melakukan perhitungan:
Untuk \(x = -3\)
\(f(-3) = -2(-3)^2\: -\:4(-3) +6\)
\(-18 + 12 +6 = \color{blue} 0\)
Tandai titik-titik (-3, 0), (-2, 6), (-1, 8), (0, 6), (1, 0) pada diagram cartesius kemudian hubungkan semua titik tersebut sehingga diperoleh gambar grafik \(f(x) = -2x^2\: -\: 4x +6\) seperti di bawah ini.
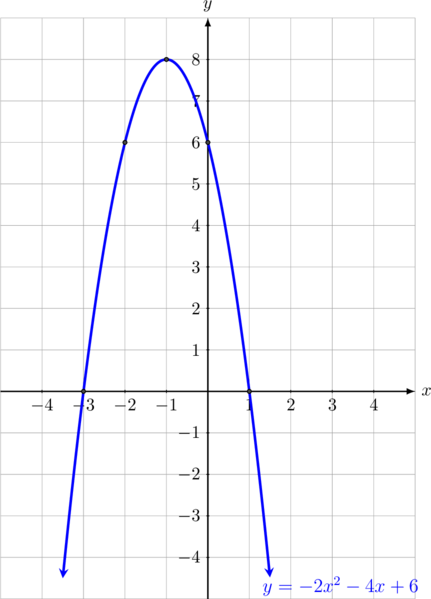
Berikut ini adalah karakteristik grafik \(f(x) = -2x^2\: -\: 4x +6\)
- berbentuk parabola yang terbuka ke bawah, karena nilai \(a < 0\)
- memiliki titik balik minimum di \((-1,8)\)
- memotong sumbu \(x\) di titik \((-3, 0) \text{ dan } (1, 0)\)
- memotong sumbu \(y\) di titik \((0,6)\)
Membuat sketsa grafik fungsi kuadrat
Soal 1
Sketsalah grafik fungsi \(f(x) = \dfrac{1}{4}x^2 + \dfrac{1}{2}x \:- \:\dfrac{15}{4}\)
Langkah 1: mencari titik potong dengan sumbu \(y\)
Titik potong dengan sumbu \(y\) diperoleh jika \(x = 0\)
\(y = \dfrac{1}{4}(0)^2 + \dfrac{1}{2}(0) – \dfrac{15}{4}\)
\(y = – \dfrac{15}{4}\)
Titik potong dengan sumbu \(y\) berada di \((0, – \dfrac{15}{4})\)
Langkah 2: mencari titik potong dengan sumbu \(x\)
Titik potong dengan sumbu \(x\) diperoleh jika \(y= 0\)
\(0 = \dfrac{1}{4}x^2 + \dfrac{1}{2}x – \dfrac{15}{4}\)
(kalikan kedua ruas dengan 4)
\(0 = x^2 + 2x \:- \:15\)
\(0 = (x + 5)(x \:- \:3)\)
\(x + 5 = 0 \rightarrow x = – 5\)
\(x -3 = 0 \rightarrow x = 3\)
Jadi titik potong dengan sumbu \(x\) berada di \((-5, 0)\text{ dan } (3, 0)\)
Langkah 3: mencari titik puncak parabola\((x_p, y_p)\)
\(y= \dfrac{1}{4}x^2 + \dfrac{1}{2}x – \dfrac{15}{4}\)
\(a = \frac{1}{4}, \: b = \frac{1}{2}, \: c = -\frac{15}{4}\)
\(\bbox[yellow, 5px] {x_p = -\dfrac{b}{2a}}\)
\(x_p = -\dfrac{\frac{1}{2}}{2( \frac{1}{4})} = -1\)
Untuk mencari \(y_p\) substitusikan nilai \(x_p = -1\) ke persamaan fungsi kuadrat
\(y_p= \dfrac{1}{4}(-1)^2 + \dfrac{1}{2}(-1) – \dfrac{15}{4}\)
\(y_p= \dfrac{1}{4} – \dfrac{2}{4}- \dfrac{15}{4}\)
\(y_p= -4\)
Jadi titik puncak parabola berada di \((-1, -4)\)
Titik \((-1, -4)\) dinamakan juga titik balik minimum karena bentuk parabola yang terbuka ke atas
Langkah 4: Menggambar
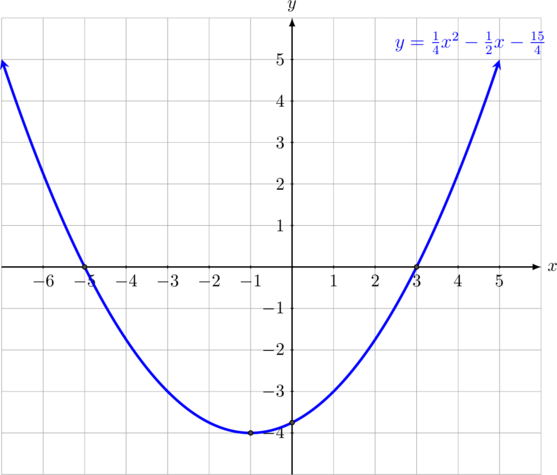
Soal 2
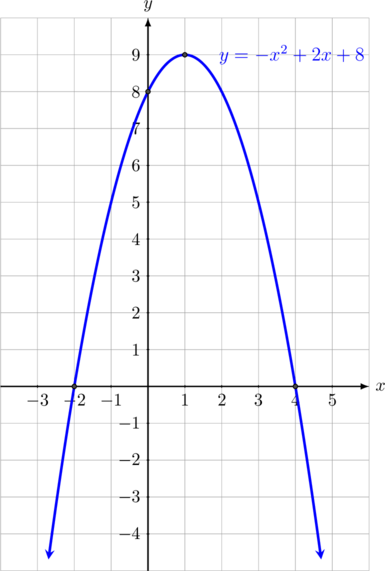
Sketsalah grafik fungsi \(f(x) = -x^2 + 2x + 8\)
Langkah 1: mencari titik potong dengan sumbu \(y\)
Titik potong dengan sumbu \(y\) diperoleh jika \(x = 0\)
\(y = -(0)^2 + 2(0) + 8\)
\(y = 8\)
Titik potong dengan sumbu \(y\) berada di \((0, 8)\)
Langkah 2: mencari titik potong dengan sumbu \(x\)
Titik potong dengan sumbu \(x\) diperoleh jika \(y= 0\)
\(0 = -x^2 + 2x + 8\)
(kalikan kedua ruas dengan -1)
\(0 = x^2 – 2x – 8\)
\(0 = (x -4)(x + 2)\)
\(x – 4 = 0 \rightarrow x = 4\)
\(x + 2 = 0 \rightarrow x = -2\)
Jadi titik potong dengan sumbu \(x\) berada di \((-2, 0)\text{ dan } (4, 0)\)
Langkah 3: mencari titik puncak parabola\((x_p, y_p)\)
\(y= -x^2 + 2x + 8\)
\(a = -1, \: b = 2, \: c = 8\)
\(\bbox[yellow, 5px] {x_p = -\dfrac{b}{2a}}\)
\(x_p = -\dfrac{2}{2( -1)} = 1\)
Untuk mencari \(y_p\) substitusikan nilai \(x_p = 1\) ke persamaan fungsi kuadrat
\(y_p= -1^2 + 2(1) + 8\)
\(y_p= -1 + 2 + 8\)
\(y_p= 9\)
Jadi titik puncak parabola berada di \((1, 9)\)
Titik \((1, 9)\) dinamakan juga titik balik maksimum karena bentuk parabola yang terbuka ke bawah
Langkah 4: Menggambar