Diketahui puncak parabola \((x_p, y_p)\) dan sebuah titik yang lain
\(\bbox[yellow, 5px] {y = a(x-x_p)^2 + y_p}\)
Contoh:
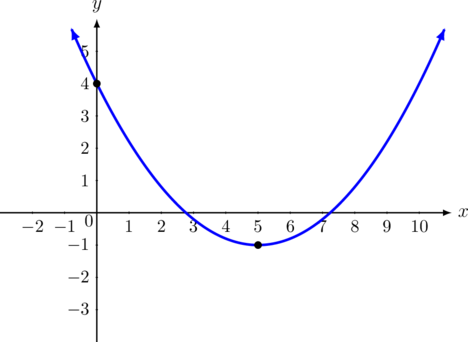
Fungsi kuadrat di bawah ini memiliki titik balik minimum di \((5, -1)\) dan melalui titik potong dengan sumbu \(y\) di \((0, 4)\). Tentukan rumus fungsi kuadrat tersebut.
Penyelesaian:
\((x_p, y_p) = (5, -1)\)
\(y = a(x-x_p)^2 + y_p\)
\(y = a(x-5)^2 -1\)
Untuk mencari nilai \(a\) substitusikan titik \((0, 4)\)
\(4 = a(0 – 5)^2 – 1\)
\(4 = 25a – 1\)
\(4 + 1 = 25a\)
\(5 = 25a\)
\(a = \dfrac{5}{25} = \dfrac{1}{5}\)
Substitusikan kembali nilai \(a = \dfrac{1}{5}\) ke persamaan \(y = a(x-5)^2 -1\)
\(y = \dfrac{1}{5}(x-5)^2 -1\)
\(y = \dfrac{1}{5}(x^2 – 10x + 25) – 1\)
\(y = \dfrac{1}{5}x^2 – 2x + 5 – 1\)
\(y = \dfrac{1}{5}x^2 – 2x + 4\)
Jadi persamaan fungsi kuadratnya adalah \(y = \dfrac{1}{5}x^2 – 2x + 4\)
Diketahui dua titik potong dengan sumbu \(x\) yaitu \((x_1, 0), (x_2, 0)\) dan sebuah titik yang lain
\(\bbox[yellow, 5px] {y = a(x – x_1)(x-x_2)}\)
Contoh:
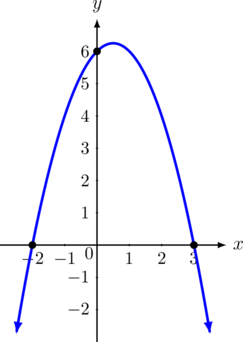
Fungsi kuadrat di bawah ini memiliki titik potong dengan sumbu \(x\) di \((-2,0)\) dan \((3,0)\), serta melalui titik potong dengan sumbu \(y\) di \((0, 6)\). Tentukan rumus fungsi kuadrat tersebut.
Penyelesaian:
Titik potong kurva dengan sumbu \(x\) di \((-2,0)\) dan \((3,0)\)
\(y = a(x – x_1)(x-x_2)\)
\(y = a(x – (-2))(x-3)\)
\(y = a(x +2)(x-3)\)
Untuk mencari nilai \(a\) substitusikan titik \((0, 6)\)
\(6 = a(0 +2)(0-3)\)
\(6 = a(-6)\)
\(a = \dfrac{6}{-6} = -1\)
Substitusikan kembali nilai \(a = -1\) ke persamaan \(y = a(x +2)(x-3)\)
\(y = -(x +2)(x-3)\)
\(y = -(x^2-3x+2x-6)\)
\(y = -(x^2-x-6)\)
\(y = -x^2 + x + 6\)
Jadi persamaan fungsi kuadratnya adalah \(y = -x^2 + x + 6\)
Diketahui tiga titik acak \((x_1, y_1), (x_2, y_2), \text{ dan } (x_3, y_3)\)
\(\bbox[yellow, 5px] {y = ax^2 + bx + c}\)
Contoh:
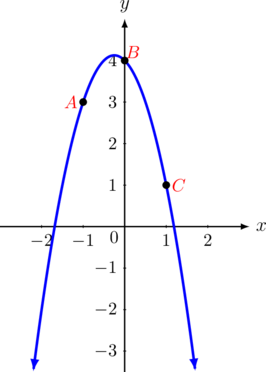
Fungsi kuadrat di bawah ini melalui titik \(A(-1,3), B(0,4), \text{ dan } C(1,1)\). Tentukan rumus fungsi kuadrat tersebut.
Penyelesaian:
Substitusikan masing-masing titik ke persamaan umum \(y = ax^2 + bx + c\)
\(A(-1,3)\rightarrow 3 = a(-1)^2 + b(-1) + c\)
\(3 = a – b + c \dotso\dotso (1)\)
\(B(0,4)\rightarrow 4 = a(0)^2 + b(0) + c\)
\(c = 4\dotso\dotso (2)\)
\(C(1,1)\rightarrow 1 = a(1)^2 + b(1) + c\)
\(1 = a + b + c\dotso\dotso (3)\)
Substitusikan nilai \(c = 4\) ke persamaan (1) dan (2)
\(3 = a – b + 4\)
\(a- b = 3 – 4\)
\(a – b = -1\dotso\dotso (4)\)
\(1 = a + b + 4\)
\(a + b = 1- 4\)
\(a + b = -3\dotso\dotso (5)\)
Eliminasi \(b\) dengan cara menjumlahkan persamaan (4) dan (5)
sehingga diperoleh nilai \(a = -2\) dan \(b = -1\)
Substitusikan nilai \(a, b, \text{ dan } c\) ke persamaan umum \(y = ax^2 + bx + c\)
\(y = -2x^2 -x +4\)
Jadi, persamaan fungsi kuadratnya adalah \(y = -2x^2 -x +4\)
