SOAL
Perhatikan gambar berikut:
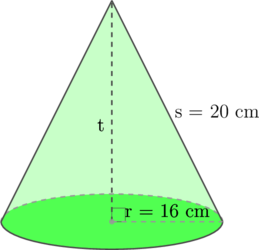
Volume kerucut di atas adalah… cm³
Pembahasan:
Langkah 1 Menghitung tinggi kerucut
Tinggi kerucut dapat kita hitung dengan menggunakan rumus pythagoras
\(t^2 + r^2 = s^2\)
\(t^2 + 16^2 = 20^2\)
\(t^2 + 256 = 400\)
\(t^2 = 400 – 256 \)
\(t^2 = 144\)
\(t = \sqrt{144} = 12 \text{ cm}\)
Langkah 2 Menghitung volume kerucut
\(\text{Volume kerucut } = \dfrac{1}{3}\pi r^2 t\)
\(\dfrac{1}{\cancelto{1}{3}}\cdot \dfrac{22}{7} \cdot 16^2 \cdot \cancelto{4}{12}\)
\(\dfrac{22}{7}\cdot 256 \cdot 4\)
\(\dfrac{22528}{7}\)
\(3218, 29 \text{ cm}^3\)
SOAL
Benda padat di bawah ini terbentuk dari dua buah kerucut yang identik. Total luas permukaan benda padat tersebut adalah… cm²
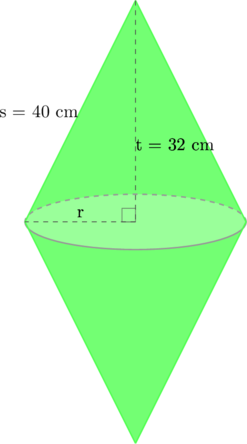
Pembahasan:
Langkah 1 Menghitung panjang jari-jari alas kerucut
Jari-jari kerucut dapat kita hitung dengan menggunakan rumus pythagoras
\(t^2 + r^2 = s^2\)
\(32^2 + r^2 = 40^2\)
\(1024 + r^2 = 1600\)
\(r^2 = 1600 – 1024\)
\(r^2 = 576\)
\(r= \sqrt{576} = 24 \text{ cm}\)
Langkah 2 Menghitung luas permukaan benda padat
Luas permukaan benda padat tersebut adalah 2 kali luas selimut kerucut
\(\text{Luas permukaan benda} = 2\times \pi r s\)
\(2 \times 3,14\cdot 24 \cdot 40\)
\(6028,8 \text{ cm}^2\)
SOAL
Sebuah kerucut akan dibuat dari karton yang berbentuk setengah lingkaran seperti pada gambar di bawah ini. Volume kerucut yang terbentuk adalah… cm³
\((\pi = \dfrac{22}{7}, \sqrt{3} = 1,732)\)
[
Pembahasan:
Langkah 1 Menghitung jari-jari alas kerucut yang terbentuk
Luas karton (luas setengah lingkaran) akan sama dengan luas selimut kerucut yang terbentuk
Jari-jari karton (R) = \(\frac{1}{2}\times 56 = 28 \text{ cm}\)
Jari-jari karton ini nantinya akan menjadi garis pelukis kerucut yang terbentuk, sehingga \(s = 28 \text{ cm}\)
Luas setengah lingkaran = luas selimut kerucut
\(\dfrac{1}{2}\cdot \pi \cdot \text{R}^2 = \pi r s\)
\(\dfrac{1}{2}\cdot \cancel{\pi} \cdot \cancel{28} \cdot 28 = \cancel{\pi} \cdot r \cdot \cancel{28}\)
\(14 = r\)
Jadi, jari-jari kerucut yang terbentuk = 14 cm
Langkah 2 Menghitung tinggi kerucut yang terbentuk
Tinggi kerucut dapat kita hitung dengan menggunakan rumus pythagoras
\(t^2 + r^2 = s^2\)
\(t^2 + 14^2 = 28^2\)
\(t^2 + 196 = 784\)
\(t^2 = 784 – 196 \)
\(t^2 = 588\)
\(t = \sqrt{588}\)
\(t = \sqrt{196 \times 3} = 14\sqrt{3} \text{ cm}\)
Langkah 3 Menghitung volume kerucut
\(\text{Volume kerucut } = \dfrac{1}{3}\pi r^2 t\)
\(\dfrac{1}{3}\cdot \dfrac{22}{\cancelto{1}{7}} \cdot 14^2 \cdot \cancelto{2}{14}\sqrt{3}\)
\(\dfrac{1}{3}\cdot \dfrac{22}{\cancelto{1}{7}} \cdot 14^2 \cdot \cancelto{2}{14}\sqrt{3}\)
\(\dfrac{8624\sqrt{3}}{3} \text{ cm}^3\)
\(\dfrac{8624\times 1,732}{3} \text{ cm}^3\)
\(\approx 4979 \text{ cm}^3\)
SOAL
Sebuah kerucut memiliki luas alas sebesar 314 cm² dan tinggi 24 cm. Luas selimut kerucut tersebut adalah … cm². (Gunakan \(\pi = 3,14\))
Pembahasan:
Langkah 1 Menghitung jari-jari alas kerucut
\(\text{Luas alas} = \pi r^2\)
\(314 = 3,14\cdot r^2\)
\(314 \div 3,14 = r^2\)
\(100 = r^2\)
\(r = \sqrt{100} = 10 \text{ cm}\)
Langkah 2 Menghitung panjang garis pelukis
Panjang garis pelukis dapat kita hitung dengan menggunakan rumus pythagoras
\(t^2 + r^2 = s^2\)
\(24^2 + 10^2 = s^2\)
\(576 + 100 = s^2\)
\(676 = s^2\)
\(s = \sqrt{676} = 26 \text{ cm}\)
Langkah 3 Menghitung luas selimut kerucut
\(\text{Luas selimut kerucut} = \pi r s\)
\(3,14 \cdot 10 \cdot 26\)
\(816,4 \text{ cm}^2\)
SOAL
Sebuah kerucut memiliki panjang garis pelukis 10 cm dan luas selimut \(60\pi\text{ cm}^2\). Tinggi kerucut tersebut adalah…
Pembahasan:
Langkah 1 Menghitung jari-jari alas kerucut
\(\text{Luas selimut } = \pi r s\)
\(\cancelto{6}{60} \cancel{\pi} = \cancel{\pi} \cdot r \cdot \cancelto{1}{10}\)
\(r = 6 \text{ cm}\)
Langkah 2 Menghitung tinggi kerucut
Tinggi kerucut dapat kita hitung dengan menggunakan rumus pythagoras
\(t^2 + r^2 = s^2\)
\(t^2 + 6^2 = 10^2\)
\(t^2 + 36 = 100\)
\(t^2 = 100 – 36\)
\(t^2 = 64\)
\(t = \sqrt{64} = 8 \text{ cm}\)
SOAL
Sebuah topi ulang tahun berbentuk kerucut dengan diameter 30 cm dan tinggi 36 cm. Luas permukaan topi tersebut adalah…
Pembahasan:
Topi berbentuk kerucut tanpa alas, sehingga luas permukaan topi sama dengan luas selimut kerucut
Langkah 1 Menghitung panjang garis pelukis
Panjang garis pelukis dapat kita hitung dengan menggunakan rumus pythagoras
Jari-jari kerucut = \(\dfrac{1}{2}\times 30 = 15 \text{ cm}\)
\(t^2 + r^2 = s^2\)
\(36^2 + 15^2 = s^2\)
\(1296 + 225 = s^2\)
\(1521 = s^2\)
\(s = \sqrt{1521} = 39 \text{ cm}\)
Langkah 2 Menghitung luas permukaan topi
\(\text{Luas permukaan topi} = \pi r s\)
\(\dfrac{22}{7}\cdot 15 \cdot 39\)
\(\dfrac{22}{7}\cdot 585\)
\(\dfrac{12870}{7}\)
\(1838,57 \text{ cm}^2\)
SOAL
Volume kerucut terpancung di bawah ini adalah… cm³
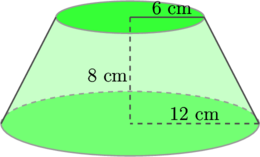
Pembahasan:
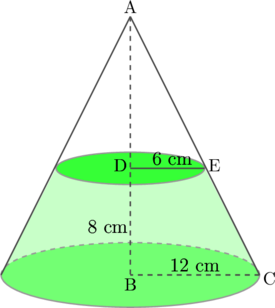
Perhatikan bahwa segitiga ADE sebangun dengan segitiga ABC
Sehingga berlaku:
\(\dfrac{\text{AD}}{\text{AB}}=\dfrac{\text{DE}}{\text{BC}}\)
\(\dfrac{\text{AD}}{\text{AD} + 8}=\dfrac{6}{12}\)
\(\dfrac{\text{AD}}{\text{AD} + 8}=\dfrac{1}{2}\:\:\:\:\:\color{blue}\text{kali silang}\)
\(2\text{AD} = \text{AD} + 8\)
\(2\text{AD} – \text{AD} = 8\)
\(\text{AD} = 8\text{ cm}\)
\(\text{Sehingga AB = 8 + 8 = 16 cm}\)
Volume kerucut terpancung dapat kita hitung dengan mengurangi volume kerucut yang besar yang berjari-jari R = 12 cm dengan volume kerucut yang kecil yang berjari-jari r = 6 cm.
Volume kerucut terpancung:
\(\dfrac{1}{3}\cdot \pi \cdot \text{ R} \cdot \text{ AB} – \dfrac{1}{3}\cdot \pi \cdot \text{ r} \cdot \text{ AD}\)
\(\dfrac{1}{\cancelto{1}{3}}\cdot \dfrac{22}{7} \cdot \cancelto{4}{12} \cdot 16 – \dfrac{1}{\cancelto{1}{3}}\cdot \dfrac{22}{7} \cdot \cancelto{2}{6} \cdot 8\)
\(\dfrac{1408}{7} – \frac{352}{7}\)
\(\dfrac{1056}{7}\text{ cm}^3\)
\(150,86\text{ cm}^3\)
SOAL
Sebuah kerucut akan dibentuk dari potongan karton di bawah ini. Tinggi kerucut yang terbentuk adalah…
\((\sqrt{2} = 1,414)\)
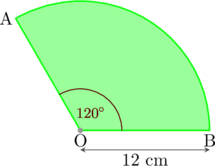
Pembahasan:
Langkah 1: Menghitung jari-jari alas kerucut yang terbentuk
Luas karton yang berbentuk juring lingkaran akan sama dengan luas selimut kerucut yang terbentuk
Jari-jari karton (R) = \(12\text{ cm}\)
Jari-jari karton ini nantinya akan menjadi garis pelukis kerucut yang terbentuk, sehingga \(s = 12\text{ cm}\)
\(\text{Luas juring = luas selimut kerucut}\)
\(\dfrac{120^{\circ}}{360^{\circ}}\cdot \pi \cdot \text{R}^2 = \pi r s\)
\(\dfrac{1}{3}\cdot \cancel{\pi} \cdot \cancel{12} \cdot 12 = \cancel{\pi} \cdot r \cdot \cancel{12}\)
\(4 = r\)
Jadi, jari-jari kerucut yang terbentuk = 4 cm
Langkah 2: Menghitung tinggi kerucut
Tinggi kerucut yang terbentuk dapat kita cari menggunakan rumus pythagoras
\(r^2 + t^2 = s^2\)
\(4^2 + t^2 = 12^2\)
\(16 + t^2 = 144\)
\(t^2 = 144 – 16\)
\(t^2 = 128\)
\(t = \sqrt{128} \text{ cm}\)
\(t = 8\sqrt{2} = 11,31\text{ cm}\)
SOAL
Sebuah kerucut memiliki keliling alas 66 cm dan tinggi 10 cm. Volume kerucut tersebut adalah…cm³. (Gunakan \(\pi = \frac{22}{7}\))
Pembahasan:
Langkah 1: Menghitung jari-jari alas kerucut
\(\text{Keliling alas} = 2\pi r\)
\(66 = 2\dfrac{22}{7}\cdot r\)
\(66 = \dfrac{44}{7}\cdot r\)
\(\cancelto{3}{66} \times \dfrac{7}{\cancelto{2}{44}} = r\)
\(r = \dfrac{21}{2}\text{ cm}\)
Langkah 2: Menghitung volume kerucut
\(\text{Volume kerucut} = \dfrac{1}{3}\pi r^2 t\)
\(\dfrac{1}{3}\dfrac{22}{\cancelto{1}{7}}\cdot \dfrac{\cancelto{3}{21}}{2} \cdot \dfrac{21}{2} \cdot 10\)
\(1155 \text{ cm}^3\)
SOAL
Sebuah kerucut memiliki luas alas \(144\pi \text{ cm}^2\) dan panjang garis pelukis \(3\sqrt{65}\text{ cm}\). Volume kerucut tersebut adalah… cm³
Pembahasan:
Langkah 1: Menghitung jari-jari alas kerucut
\(\text{Luas alas kerucut} = \pi r^2\)
\(144\cancel{\pi} = \cancel{\pi} r^2\)
\(144 = r^2\)
\(r = \sqrt{144} = 12 \text{ cm}\)
Langkah 2: Menghitung tinggi kerucut
Tinggi kerucut dapat dihitung menggunakan rumus pythagoras
\(r^2 + t^2 = s^2\)
\(12^2 + t^2 = (3\sqrt{65})^2\)
\(12^2 + t^2 = (3\sqrt{65})^2\)
\(144 + t^2 = 585\)
\(t^2 = 585 – 144\)
\(t^2 = 441\)
\(t = \sqrt{441} = 21 \text{ cm}\)
Langkah 3: Menghitung volume kerucut
\(\text{Volume kerucut} = \dfrac{1}{3} \pi r^2 t\)
\(\text{Volume kerucut} = \dfrac{1}{3}\cdot \dfrac{22}{\cancelto{1}{7}} \cdot 12^2 \cdot \cancelto{3}{21}\)
\(\text{Volume kerucut} = 3168 \text{ cm}^3\)
