Gaya Elektrostatis disebut juga Gaya Coulomb adalah gaya tarik-menarik atau tolak-menolak antara 2 buah partikel bermuatan listrik.
$$\bbox[yellow, 5px]{\text{F} = \text{k}\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}}$$
Keterangan:
- \(\text{F = Gaya Coulomb (N)}\)
- \(\text{k = } 9 \times 10^9\:\text{Nm}^2\text{C}^{-2}\)
- \(\text{Q = muatan benda (C)}\)
- \(\text{r = jarak antara dua muatan (m)}\)
Jika muatan kedua benda sejenis (+ dan +, atau − dan −) maka gaya elektrostatis yang timbul adalah tolak-menolak, tetapi jika muatan kedua benda tidak sejenis (+ dan −) maka gaya elektrostatis yang timbul adalah tarik-menarik.
Besarnya gaya elektrostatis berbanding terbalik dengan kuadrat jarak kedua muatan, dan berbanding terbalik dengan besar muatan kedua benda.
Jika kedua benda didekatkan maka gaya elektrostatis akan membesar, tetapi jika kedua benda dijauhkan maka gaya elektrostatis akan mengecil.
Contoh Soal
Dua buah partikel masing-masing bermuatan \(2,4 \:\mu\text{C}\) dan \(-3,0 \:\mu\text{C}\) terpisah sejauh 3 cm. Tentukan besar gaya elektrostatis dan juga jenisnya.
\(\text{Q}_1 = 2,4 \:\mu\text{ C} = 2,4 \times 10^{-6} \text{ C}\)
\(\text{Q}_2 = -3,0 \:\mu\text{ C} = -3,0 \times 10^{-6} \text{ C}\)
\(\text{r} = 3 \text{ cm} = 3 \times 10^{-2}\text{ m}\)
\(\text{F} = \text{k}\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}\)
\(\text{F} = 9\times 10^9\cdot \dfrac{2,4 \times 10^{-6}\cdot 3,0 \times 10^{-6}}{(3 \times 10^{-2})^2}\)
\(\text{F} = \cancel{9}\times 10^9\cdot \dfrac{7,2 \times 10^{-12}}{\cancel{9}\times 10^{-4}}\)
\(\text{F} = 7,2 \times 10^{-12 + 9 – (-4)}\)
\(\text{F} = 7,2 \times 10^1 = 72 \text{ N}\)
Karena kedua muatan tidak sejenis, maka yang timbul adalah gaya tarik-menarik
Dua buah benda bermuatan sama, yaitu sebesar \(5\times 10^{-6}\text{ C}\) saling tolak-menolak dengan gaya Coulomb sebesar 90 N. Tentukan jarak antara kedua benda tersebut.
\(\text{F} = \text{k}\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}\)
\(90 = 9\times 10^9\cdot \dfrac{5 \times 10^{-6}\cdot 5 \times 10^{-6}}{\text{r}^2}\)
\(\cancel{9}\times 10^1 = \cancel{9}\times 10^9\cdot \dfrac{25\times 10^{-12}}{\text{r}^2}\:\:\:\:\:\color{blue}\text{kali kedua ruas dengan r}^2\)
\(10\times \text{r}^2 = 25\times 10^{9 – 12}\)
bagi kedua ruas dengan 10
\(\text{r}^2 = 2,5\times 10^{-3}\)
\(\text{r}^2 = 25\times 10^{-4}\)
\(\text{r} = \sqrt{25\times 10^{-4}}\)
\(\text{r} = 5\times 10^{-2}\text{ m}\)
Diketahui gaya tarik-menarik antara buah benda bermuatan tidak sejenis \(\text{Q}_1\) dan \(\text{Q}_2\) yang terpisah sejauh \(\text{r}\) adalah \(\text{F}\). Jika masing-masing muatan diperbesar 3 kali, dan jaraknya dibuat menjadi \(\dfrac{1}{2}\) kali semula, maka tentukan besar gaya elektrostatisnya sekarang.
Misal gaya elektrostatisnya sekarang adalah \(\text{F’}\),
\(\dfrac{\text{F}}{\text{F’}} = \dfrac{ \cancel{\text{k}}\:\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}}{ \cancel{\text{k}}\:\dfrac{\text{3Q}_1\cdot \text{3Q}_2}{(\frac{1}{2}\text{r})^2}}\)
\(\dfrac{\text{F}}{\text{F’}} = \dfrac{\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}}{\dfrac{9\text{Q}_1\cdot \text{Q}_2}{\frac{1}{4}\text{r}^2}}\)
\(\dfrac{\text{F}}{\text{F’}} = \dfrac{\cancel{\dfrac{\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}}}{36\cdot\cancel{\dfrac{\cdot\text{Q}_1\cdot \text{Q}_2}{\text{r}^2}}}\)
\(\dfrac{\text{F}}{\text{F’}} = \dfrac{1}{36}\)
Kali silang
\(\text{F’} = 36\text{F}\)
Jadi gaya elektrostatisnya sekarang menjadi 36 kali semua
Dua buah partikel A dan B bermuatan listrik masing-masing \(+9 \:\mu\text{C}\) dan \(-25 \:\mu\text{C}\) terpisah sejauh 10 cm. Tentukan dimana partikel positif C harus diletakkan dari partikel A dan B agar resultan gaya elektrostatis di C sama dengan nol.
Karena muatan partikel A dan B tidak sejenis maka posisi partikel C harus diletakkan di luar garis AB dekat dengan muatan yang nilainya kecil (dekat dengan A).
Agar resultan gaya elektrostatis di C sama dengan nol maka \(\text{F}_{\text{CA}} = \text{F}_{\text{CB}}\).

\(\text{F}_{\text{CA}}\) = gaya tolak-menolak antara partikel C dan partikel A
\(\text{F}_{\text{CB}}\) = gaya tarik-menarik antara partikel C dan partikel B
\(\text{F}_{\text{CA}} = \text{F}_{\text{CB}}\)
\(\cancel{\text{k}}\dfrac{\cancel{\text{Q}_c}\cdot \text{Q}_a}{\text{r}_{ca}^2} = \cancel{\text{k}}\dfrac{\cancel{\text{Q}_c}\cdot \text{Q}_b}{\text{r}_{cb}^2}\)
\(\dfrac{9 \mu \text{C}}{x^2} = \dfrac{25 \mu \text{C}}{10^2}\)
Kedua ruas diberi akar
\(\sqrt{\dfrac{9 \mu \text{C}}{x^2}} = \sqrt{\dfrac{25 \mu \text{C}}{10^2}}\)
\(\dfrac{3}{x} = \dfrac{5}{10}\)
Kali silang
\(5x = 30\)
\(x = \dfrac{30}{5} = 6 \text{ cm}\)
Jadi posisi partikel C adalah 6 cm di sebelah kiri partikel A
Dua buah partikel A dan B bermuatan listrik masing-masing \(+36 \:\mu\text{C}\) dan \(+49 \:\mu\text{C}\) terpisah sejauh 12 cm. Tentukan dimana partikel positif C harus diletakkan dari partikel A dan B agar resultan gaya elektrostatis di C sama dengan nol.
Karena muatan partikel A dan B sejenis maka posisi partikel C harus diletakkan di antara A dan B.
Agar resultan gaya elektrostatis di C sama dengan nol maka \(\text{F}_{\text{CA}} = \text{F}_{\text{CB}}\).

\(\text{F}_{\text{CA}}\) = gaya tolak-menolak antara partikel C dan partikel A
\(\text{F}_{\text{CB}}\) = gaya tolak-menolak antara partikel C dan partikel B
\(\text{F}_{\text{CA}} = \text{F}_{\text{CB}}\)
\(\cancel{\text{k}}\dfrac{\cancel{\text{Q}_c}\cdot \text{Q}_a}{\text{r}_{ca}^2} = \cancel{\text{k}}\dfrac{\cancel{\text{Q}_c}\cdot \text{Q}_b}{\text{r}_{cb}^2}\)
\(\dfrac{36 \mu \text{C}}{x^2} = \dfrac{49 \mu \text{C}}{(12-x)^2}\)
Kedua ruas diberi akar
\(\sqrt{\dfrac{36 \mu \text{C}}{x^2}} = \sqrt{\dfrac{49 \mu \text{C}}{(12-x)^2}}\)
\(\dfrac{6}{x} = \dfrac{7}{(12-x)}\)
Kali silang
\(7x = 6(12-x)\)
\(7x = 72 – 6x\)
\(7x + 6x = 72\)
\(13x = 72\)
\(x = \dfrac{72}{13} = 5,54 \text{ cm}\)
Jadi posisi partikel C adalah 5,54 cm di sebelah kanan partikel A
Tiga buah partikel A, B, dan C diletakkan pada setiap titik sudut segitiga siku-siku, seperti pada gambar di bawah ini.
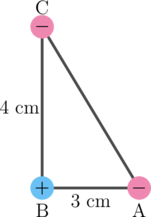
\(\text{Q}_{\text{A}} = -1 \mu \text{C}\)
\(\text{Q}_{\text{B}} = +2 \mu \text{C}\)
\(\text{Q}_{\text{C}} = -8 \mu \text{C}\)
Jarak antara A dan B = 3 cm dan jarak antara B dan C = 4 cm.
Tentukan besar resultan gaya elektrostatis di B
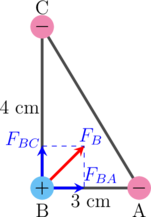
\(\text{F}_{\text{BA}}\) = gaya tarik-menarik antara partikel B dan partikel A
\(\text{F}_{\text{BA}} = \text{k}\dfrac{\text{Q}_B\cdot \text{Q}_A}{\text{r}_{\text{BA}}^2}\)
\(\text{F}_{\text{BA}}= 9\times 10^9\cdot \dfrac{2\times 10^{-6}\cdot 1\times 10^{-6}}{(3\times 10^{-2})^2}\)
\(\text{F}_{\text{BA}}= \cancel{9}\times 10^9\cdot \dfrac{2\times 10^{-12}}{\cancel{9}\times 10^{-4}}\)
\(\text{F}_{\text{BA}}= 2\times 10^{9 – 12 – (-4)}\)
\(\text{F}_{\text{BA}} = 2\times 10 = 20\text{ N}\)
\(\text{F}_{\text{BC}}\) = gaya tarik-menarik antara partikel B dan partikel C
\(\text{F}_{\text{BC}} = \text{k}\dfrac{\text{Q}_B\cdot \text{Q}_C}{\text{r}_{\text{BC}}^2}\)
\(\text{F}_{\text{BC}} = 9\times 10^9\cdot \dfrac{2\times 10^{-6}\cdot 8\times 10^{-6}}{(4\times 10^{-2})^2}\)
\(\text{F}_{\text{BC}} = 9\times 10^9\cdot \dfrac{\cancel{16}\times 10^{-12}}{\cancel{16}\times 10^{-4}}\)
\(\text{F}_{\text{BC}} = 9\times 10^{9 – 12 – (-4)}\)
\(\text{F}_{\text{BC}} = 9\times 10 = 90\text{ N}\)
Resultan gaya elektrostatis di B adalah \(\text{F}_{\text{B}}\),
\(\text{F}_{\text{B}} = \sqrt{\text{F}_{\text{BA}}^2 + \text{F}_{\text{BC}}^2}\)
\(\text{F}_{\text{B}} = \sqrt{20^2 + 90^2}\)
\(\text{F}_{\text{B}} = \sqrt{400 + 8100}\)
\(\text{F}_{\text{B}} = \sqrt{8500}\)
\(\text{F}_{\text{B}} = 10\sqrt{85}\text{ N}\)
Jadi besar resultan gaya elektrostatis di B adalah \(10\sqrt{85}\text{ N}\)
