Soal 01
Ani mengurutkan bilangan asli kelipatan 5 dari yang terkecil ke terbesar, sedangkan Budi mengurutkan bilangan asli kelipatan 4 dari yang terkecil ke terbesar.
Jumlah bilangan Ani urutan ke-18 dan bilangan Budi urutan ke-22 adalah…
(A) 170
(B) 175
(C) 178
(D) 180
Jawaban: C. 178
Yang termasuk bilangan asli: 1, 2, 3, 4, 5, 6, 7 dan seterusnya
Bilangan yang diurutkan oleh Ani adalah bilangan asli kelipatan 5 yaitu: 5, 10, 15, 20, 25, 30, …
Bilangan yang diurutkan oleh Budi adalah bilangan asli kelipatan 4 yaitu: 4, 8, 12, 16, 20, 24, …
Bilangan Ani pada urutan ke-18 adalah 5 × 18 = 90
Bilangan Budi pada urutan ke-22 adalah 4 × 22 = 88
Jumlah bilangan Ani urutan ke-18 dan bilangan Budi urutan ke-22 adalah 90 + 88 = 178
Soal 02
Diketahui tiga orang sahabat, yaitu Dika, Elly, dan Farhan. Dika paling muda dan Farhan paling tua.
Usia Dika dan Elly berselisih 2 tahun, sedangkan usia Elly dan Farhan berselisih 2 tahun.
Lima tahun kemudian, jumlah usia mereka menjadi 90 tahun.
Jumlah usia Dika dan Farhan saat ini adalah … tahun.
(A) 50
(B) 60
(C) 62
(D) 64
Jawaban: A. 50
Misal:
D = usia Dika sekarang (paling muda)
E = usia Elly saat ini
F = usia Farhan saat ini (paling tua)
Usia Dika dan Elly berselisih 2 tahun, maka persamaannya:
E − D = 2
E = 2 + D (Persamaan 1)
Esia Elly dan Farhan berselisih 2 tahun, maka persamaannya:
F − E = 2
F = 2 + E
Gantilah E dengan 2 + D sesuai persamaan (1) tadi
F = 2 + (2 + D)
F = 4 + D (Persamaan 2)
Lima tahun kemudian, jumlah usia mereka menjadi 90 tahun.
(D + 5) + (E + 5) + (F + 5) = 90
D + E + F + 15 = 90
D + E + F = 75 (Persamaan 3)
Selanjutnya, substitusikan persamaan (1) dan (2) ke persamaan (3)
D + E + F = 75
D + (2 + D) + (4 + D) = 75
6 + 3D = 75
3D = 75 − 6
3D = 69
D = 69 ÷ 3
D = 23
Substitusi nilai D = 23 ke persamaan (2)
F = 4 + D
F = 4 + 23
F = 27
Jumlah usia Dika dan Farhan saat ini adalah D + F = 23 + 27 = 50 tahun.
Soal 03
Jika \(a \:\triangle\: b = \) jumlah dari sisa dan hasil bagi ketika \(a\) dibagi \(b\), hasil \(2007\: \triangle \: 8 = \dotso\)
(A) 250
(B) 256
(C) 257
(D) 258
Jawaban: C. 257
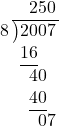
Sisa = 7 (angka paling bawah dari pembagian bersusun)
Hasil bagi = 250 (tertulis di paling atas)
\(2007\: \triangle \: 8 = 7 + 250 = 257\)
Soal 04
Hasil operasi campuran bilangan berikut:
\(\left(\dfrac{1}{4}\:-\:\dfrac{1}{5}\right)\times 40 \% + 0,25 \times 4,4\)
dalam bentuk desimal adalah…
(A) 1,11
(B) 1,12
(C) 1,13
(D) 1,14
Jawaban: B. 1,12
\(\left(\dfrac{1}{4}\:-\:\dfrac{1}{5}\right)\times 40 \% + 0,25 \times 4,4\)
\(\left(\dfrac{5}{20}\:-\:\dfrac{4}{20}\right)\times \dfrac{40}{100} + \dfrac{25}{100} \times \dfrac{44}{10}\)
\(\dfrac{1}{\cancel{20}} \times \dfrac{\cancelto{2}{40}}{100} + \dfrac{1100}{1000}\)
\(\dfrac{2}{100} + \dfrac{110}{100}\)
\(\dfrac{112}{100}\)
\(1,12\)
Soal 05
Tentukan nilai \(x\) yang memenuhi persamaan:
\(2017\:-\:7\times 2 \div x \times 5 = 267\)
(A) 5
(B) 25
(C) 0,04
(D) 0,0016
Jawaban: C. 0,04
\(2017\:-\:7\times 2 \div x \times 5 = 267\)
Kerjakan bagian perkalian terlebih dahulu
\(2017\:-\:14\div x \times 5 = 267\)
\(2017\:-\:70\div x= 267\)
Dapat ditulis
\(2017\:-\:267 = 70\div x\)
\(1750 = 70\div x\)
Dapat ditulis
\(x = \dfrac{70}{1750}\)
\(x = 0,04\)
Soal 06
Manakah yang memiliki nilai terkecil?
(A) \(\dfrac{3 + 4}{6 + 8}\)
(B) \(\dfrac{4\:-\:3}{8\:-\:6}\)
(C) \(\dfrac{3 \times 4}{8 \times 6}\)
(D) \(\dfrac{3 \div 4}{8 \div 6}\)
Jawaban: C
Kita hitung satu persatu
(A)
\(\dfrac{3 + 4}{6 + 8} = \dfrac{7}{14}\)
\(\dfrac{1}{2} = 0,5\)
(B)
\(\dfrac{4\:-\:3}{8\:-\:6} = \dfrac{1}{2} = 0,5\)
(C)
\(\dfrac{3 \times 4}{8 \times 6} = \dfrac{12}{48}\)
\(\dfrac{1}{4} = 0,25\)
(D)
\(\dfrac{3 \div 4}{8 \div 6}\)
\(\dfrac{\frac{3}{4}}{\frac{8}{6}}\)
\(\dfrac{3}{4} \times \dfrac{6}{8}\)
\(\dfrac{18}{32}\)
\(\dfrac{9}{16} = 0,5625\)
Jadi, nilai terkecil adalah C. 0,25
Soal 07
Sederhanakan bentuk pecahan berikut: \(\dfrac{1}{2 + \dfrac{3}{4 + \dfrac{5}{6}}}\)
(A) \(\dfrac{2}{33}\)
(B) \(\dfrac{29}{76}\)
(C) \(2\dfrac{1}{12}\)
(D) \(2\dfrac{18}{29}\)
Jawaban: B
\(\dfrac{1}{2 + \dfrac{3}{4 + \dfrac{5}{6}}}\)
Kerjakan dari paling bawah
\(\dfrac{1}{2 + \dfrac{3}{\dfrac{24}{6} + \dfrac{5}{6}}}\)
\(\dfrac{1}{2 + \dfrac{3}{\dfrac{29}{6}}}\)
\(\dfrac{1}{2 + 3 \times \dfrac{6}{29}}\)
\(\dfrac{1}{2 + \dfrac{18}{29}}\)
\(\dfrac{1}{\dfrac{58}{29} + \dfrac{18}{29}}\)
\(\dfrac{1}{\dfrac{76}{29}}\)
\(\dfrac{29}{76}\)
Soal 08
Joko meletakkan kelereng-kelerengnya dengan posisi sebagai berikut:
![]()
- Kelereng pertama diletakkan pada jarak 2 cm dari titik P
- Kelereng kedua diletakkan pada jarak 4 cm dari kelereng pertama
- Kelereng ketiga diletakkan pada jarak 8 cm dari kelereng kedua, demikian seterusnya
Jarak kelereng keenam dari titik P adalah…
(A) 120 cm
(B) 124 cm
(C) 126 cm
(D) 128 cm
Jawaban: C. 126 cm
Jarak kelereng pertama dari P adalah 2 cm
Jarak kelereng kedua dari P adalah 2 + 4 = 6 cm
Jarak kelereng ketiga dari P adalah 2 + 4 + 8 = 14 cm
Perhatikan pola bilangannya (angka berikutnya adalah 2 kali angka sebelumnya)
Jarak kelereng keempat dari P adalah 2 + 4 + 8 + 16 = 30
Jarak kelereng kelima dari P adalah 2 + 4 + 8 + 16 + 32 = 62
Jarak kelereng keenam dari P adalah 2 + 4 + 8 + 16 + 32 + 64 = 126
Soal 09
Diketahui \(x \times y \times z = 2015\), dengan \(x, y, \text{ dan } z\) adalah bilangan bulat yang memenuhi \(x < y < z\). Tentukan banyaknya semua kemungkinan tripel \((x, y, z)\) yang memenuhi.
(A) 1
(B) 4
(C) 5
(D) 27
Jawaban: B. 4
Kemungkinan tripel \((x, y, z)\) yang memenuhi \(x < y < z\) adalah:
Kemungkinan pertama
Faktorisasi prima dari 2015 adalah: 5 × 13 × 31
\(2015 = 5 \times 13 \times 31\)
\(5 < 13 < 31\)
Kemungkinan kedua
\(2015 = -403 \times -5 \times 1\)
\(-403 < -5 < 1\)
Kemungkinan ketiga
\(2015 = -155 \times -13 \times 1\)
\(-155 < -13 < 1\)
Kemungkinan keempat
\(2015 = -65 \times -31 \times 1\)
\(-65 < -31 < 1\)
Jadi, banyaknya semua kemungkinan tripel \((x, y, z)\) yang memenuhi adalah 4.
Soal 10
Hasil dari \(\dfrac{2007 + 2006 \times 2008}{2007 \times 2008 \:-\: 1}\) adalah…
(A) 0
(B) 1
(C) 2
(D) 3
Jawaban: B.1
\(\dfrac{2007 + 2006 \times 2008}{2007 \times 2008 \:-\: 1}\)
\(\dfrac{2007 + (2007 \:-\:1) \times (2007 + 1)}{2007 \times (2007 + 1) \:-\: 1}\)
Gunakan rumus \(\color{blue} (a \:-\:b)(a + b) = a^2 \:-\:b^2\) untuk menghitung \((2007 \:-\:1) \times (2007 + 1)\)
\((2007 \:-\:1) \times (2007 + 1) = 2007^2 \:-\:1^2\)
\(\dfrac{2007 + 2007^2\:-\:1}{2007^2 + 2007 \:-\: 1}\)
\(\dfrac{\cancel{2007^2 + 2006}}{\cancel{2007^2 + 2006}} = 1\)
Soal 11
Pada akhir tahun 2012, sebanyak \(\dfrac{3}{4}\) dari jumlah guru di suatu Sekolah Dasar adalah wanita. Pada permulaan tahun 2023, sekolah tersebut menerima 5 orang pria guru sehingga banyaknya pria guru seluruhnya menjadi 17 orang. Banyaknya wanita guru yang mengajar di Sekolah Dasar tersebut pada akhir tahun 2012 adalah…
(A) 30 orang
(B) 36 orang
(C) 40 orang
(D) 48 orang
Jawaban: B
Soal 12
Empat puluh persen peserta didik di suatu sekolah adalah laki-laki. Sebanyak 30% laki-laki dan 30% perempuan tidak memakai seragam batik. Jika diketahui ada 280 peserta didik memakai seragam batik, maka seluruh peserta didik yang ada di sekolah adalah…
(A) 200 anak
(B) 350 anak
(C) 400 anak
(D) 420 anak
Jawaban: C
Soal 13
Sebuah kotak besar dapat menampung 12 buah kelereng dan sebuah kotak kecil dapat menampung 5 buah kelereng. Jika jumlah kelereng yang tertampung ada sebanyak 99 buah, jumlah kotak besar yang mungkin ada sebanyak…
(A) 3
(B) 5
(C) 6
(D) 7
Jawaban: D
Soal 14
Sepeda Sirkus memiliki ukuran ban yang berbeda, ban depan berjari-jari 56 cm dan ban belakang berjari-jari 70 cm. Jika sepeda dikendarai dan menempuh jarak 3,52 km. Maka roda depan dan roda belakang masing-masing berputar sebanyak… putaran.
(A) 1000 dan 800
(B) 800 dan 1000
(C) 1200 dan 800
(D) 1200 dan 1000
Jawaban: A
Soal 15
Tiga buah garis saling memotong satu sama lain membentuk suatu segitiga.
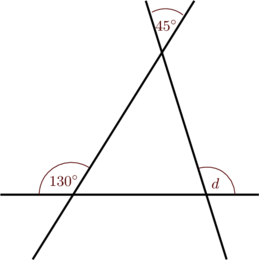
Besar sudut \(d\) adalah…
(A) \(80^{\circ}\)
(B) \(85^{\circ}\)
(C) \(90^{\circ}\)
(D) \(95^{\circ}\)
Jawaban: D
Soal 16 (HOTS)
ABCD ada sebuah persegi. Segitiga BPC adalah segitiga sama sisi. AB = BP dan CD = CP.
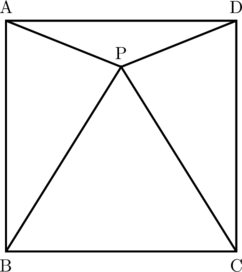
Besar sudut ADP adalah…
(A) \(10^{\circ}\)
(B) \(12^{\circ}\)
(C) \(13^{\circ}\)
(D) \(15^{\circ}\)
Jawaban: D
