Perhatikan kurva berikut:
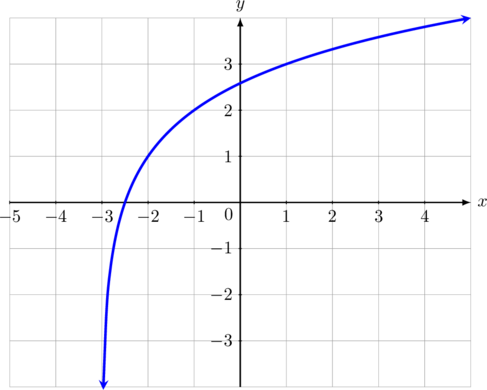
Berdasarkan gambar di atas, persamaan fungsi logaritma yang benar adalah …
(A) \(\text{f(x)} =\: ^2\log_{}{(x + 3)} + 1\)
(B) \(\text{f(x)} =\: ^2\log_{}{(x + 4)} + 1\)
(C) \(\text{f(x)} =\: ^2\log_{}{(x + 4)} + 2\)
(D) \(\text{f(x)} =\: ^2\log_{}{(x + 6)} + 2\)
(E) \(\text{f(x)} =\: ^2\log_{}{(x + 7)} + 3\)
Jawaban: A
Kurva di atas, memiliki asimtot vertikal \(x = -3\) dan melalui titik \((-2, 1)\) dan titik \((1, 3)\)
Misal persamaan kurva adalah \(\color{blue} y =\: ^a\log_{}{(x + b)} + c\)
Asimtot vertikalnya adalah \(x + b = 0\) atau ditulis \(x = – b\). Karena pada gambar asimtot vertikalnya adalah \(x = -3\) , maka nilai \(b = 3\)
Kurva melalui titik \((-2, 1)\), maka:
\(1 =\: ^a\log_{}{(-2 + 3)} + c\)
\(1 =\: ^a\log_{}{1} + c\)
\(1 = 0 + c\)
\(c = 1\)
Kurva melalui titik \((1, 3)\), maka:
\(3 =\:^a\log_{}{(1 + 3)} + 1\)
\(3 =\: ^a\log_{}{4} + 1\)
\(3\:-\:1 =\: ^a\log_{}{4}\)
\(2 =\: ^a\log_{}{4}\)
\(a^{2} = 4\)
\(a = 2\)
Persamaan fungsi logaritmanya adalah:
\(\color{blue} \text{f(x)} =\: ^2\log_{}{(x + 3)} + 1\)
Perhatikan kurva berikut:
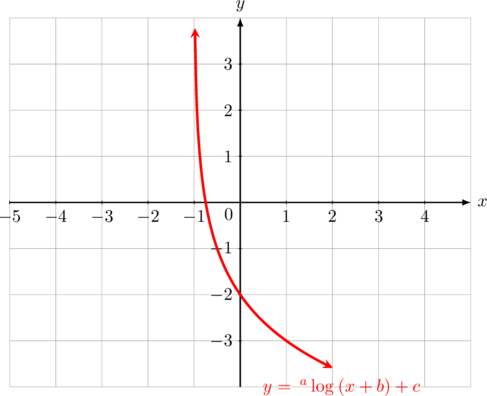
Kurva logaritma di atas dapat dinyatakan dalam bentuk \(y =\:^a\log_{}{(x + b)} + c\). Nilai dari \(2a + b + c = \dotso\)
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Jawaban: A
Kurva di atas, memiliki asimtot vertikal \(x = -1\) dan melalui titik \((0,-2)\) dan titik \((1, -3)\)
Persamaan kurva : \(\color{blue} y =\: ^a\log_{}{(x + b)} + c\)
Asimtot vertikalnya adalah \(x + b = 0\) atau ditulis \(x = – b\). Karena pada gambar asimtot vertikalnya adalah \(x = -1\) , maka nilai \(b = 1\)
Kurva melalui titik \((0,-2)\), maka:
\(-2 =\: ^a\log_{}{(0 + 1)} + c\)
\(-2 =\: ^a\log_{}{1} + c\)
\(-2 = 0 + c\)
\(c = -2\)
Kurva melalui titik \((1, -3)\), maka:
\(-3 =\:^a\log_{}{(1 + 1)} -2\)
\(-3 =\: ^a\log_{}{2} -2\)
\(-3 + 2 =\: ^a\log_{}{2}\)
\(-1 =\: ^a\log_{}{2}\)
\(a^{-1} = 2\)
\(a = \frac{1}{2}\)
Persamaan fungsi logaritmanya adalah:
\(\color{blue} \text{f(x)} =\: ^{\frac{1}{2}}\log_{}{(x + 1)} \:-\:2\)
Nilai \(2a + b + c = 2(\frac{1}{2}) + 1 \:-\:2 = 0\)
Kurva \(y =\:^3\log_{}{(3x\:-\:1)} + 3\) digeser ke atas 2 satuan dan ke kiri 4 satuan. Persamaan kurva yang baru adalah …
(A) \(y =\:^3\log_{}{(3x\:-\:10)} + 5\)
(B) \(y =\:^3\log_{}{(2x\:-\:11)} + 3\)
(C) \(y =\:^3\log_{}{(3x\:-\:11)} + 5\)
(D) \(y =\:^3\log_{}{(3x + 11)} + 5\)
(E) \(y =\:^3\log_{}{(3x + 12)} + 5\)
Jawaban: D
\(y =\:^3\log_{}{(3x\:-\:1)} + 3\)
Kurva digeser ke atas 2 satuan, menjadi:
\(y =\:^3\log_{}{3(x\:-\:\frac{1}{3})} + 3 \color{red}+ 2\)
\(y =\:^3\log_{}{3(x\:-\:\frac{1}{3})} + 5\)
Kurva digeser ke kiri 4 satuan, menjadi:
\(y =\:^3\log_{}{3(x\:-\:\frac{1}{3} \color{red}+ 4 \color{black})} + 5\)
\(y =\:^3\log_{}{3(x + \frac{11}{3})} + 5\)
\(y =\:^3\log_{}{(3x + 11)} + 5\)
Diketahui kurva \(y = \:^a\log_{}{(x + b)} + c\) melalui titik \((5, 5), (\frac{9}{2}, 4), \text{ dan } (\frac{17}{4}, 3)\). Persamaan kurva logaritma tersebut adalah …
(A) \(y = \:^2\log_{}{(x\:-\:2)} + 3\)
(B) \(y = \:^2\log_{}{(x\:-\:4)} + 3\)
(C) \(y = \:^2\log_{}{(x\:-\:4)} + 5\)
(D) \(y = \:^2\log_{}{(x + 4)} + 5\)
(E) \(y = \:^2\log_{}{(x + 4)} + 6\)
Jawaban: C
Substitusikan setiap titik pada fungsi logaritma
\((5, 5) \rightarrow 5 = \:^a\log_{}{(5 + b)} + c\dotso\dotso (1)\)
\((\frac{9}{2}, 4) \rightarrow 4 = \:^a\log_{}{(\frac{9}{2} + b)} + c\dotso\dotso (2)\)
\((\frac{17}{4}, 3) \rightarrow 3 = \:^a\log_{}{(\frac{17}{4} + b)} + c\dotso\dotso (3)\)
Kurangkan persamaan (1) dengan persamaan (2) untuk eliminasi \(c\), sehingga diperoleh:
\(1 = \:^a\log_{}{(5 + b)}\:-\: ^a\log_{}{(\frac{9}{2} + b)}\)
\(1 = \:^a\log_{}{\left(\dfrac{5 + b}{\frac{9}{2} + b}\right)}\dotso\dotso (4)\)
Kurangkan persamaan (2) dengan persamaan (3) untuk eliminasi \(c\), sehingga diperoleh:
\(1 = \:^a\log_{}{(\frac{9}{2} + b)} \:-\: ^a\log_{}{(\frac{17}{4} + b)}\)
\(1 = \:^a\log_{}{\left(\dfrac{\frac{9}{2} + b}{\frac{17}{4} + b}\right)}\dotso\dotso (5)\)
Persamaan (4) dan (5), sama-sama memiliki nilai sama dengan 1, sehingga:
\(^a\log_{}{\dfrac{5 + b}{\frac{9}{2} + b}}=\: ^a\log_{}{\dfrac{\frac{9}{2} + b}{\frac{17}{4} + b}}\)
\(\dfrac{5 + b}{\frac{9}{2} + b} = \dfrac{\frac{9}{2} + b}{\frac{17}{4} + b}\:\:\:\:\:\color{blue}\text{kali silang}\)
\((5 + b)(\frac{17}{4} + b) = (\frac{9}{2} + b)(\frac{9}{2} + b)\)
\(\frac{85}{4} + 5b + \frac{17}{4}b + \cancel{b^2} = \frac{81}{4} + 9b + \cancel{b^2}\)
\(\frac{85}{4}\:-\: \frac{81}{4} = 9b\:-\:5b\:-\:\frac{17}{4}b \)
\(1 = -\frac{1}{4}b\)
\(b = -4\)
Substitusikan nilai \(b = -4\) ke persamaan (4)
\(1 = \:^a\log_{}{\left(\dfrac{5 + b}{\frac{9}{2} + b}\right)}\)
\(1 = \:^a\log_{}{\left(\dfrac{5\:-\:4}{\frac{9}{2}\:-\:4}\right)}\)
\(1 = \:^a\log_{}{\dfrac{1}{\frac{1}{2}}}\)
\(1 = \:^a\log_{}{2}\)
\(a^1 = 2\)
\(a = 2\)
Substitusikan nilai \(a = 2\) dan \(b = -4\) ke persamaan (1)
\(5 = \:^a\log_{}{(5 + b)} + c\)
\(5 = \:^2\log_{}{(5 \:-\:4)} + c\)
\(5 = \:^2\log_{}{1} + c\)
\(5 = 0 + c\)
\(c = 5\)
Jadi persamaan kurva logaritmanya adalah \(y = \:^2\log_{}{(x\:-\:4)} + 5\)
