
Langkah-langkah menentukan bayangan titik \(\text{P}(x_1, y_1)\) ke garis \(ax + by + c = 0\)
(1) Menentukan gradien garis \(ax + by + c = 0\)
\(by = -ax \:-\: c\)
\(y = -\frac{a}{b}x \:-\: \frac{c}{b}\)
Gradien garis \(m_1\) = \(-\frac{a}{b}\)
(2) Menentukan gradien garis yang melalui titik P dan Q
Misalkan bayangan titik \(\text{P}(x_1, y_1)\) adalah \(\text{Q}(x_2, y_2)\)
Gradien garis yang melalui titik \(\text{P}(x_1, y_1)\)dan\(\text{Q}(x_2, y_2)\) adalah:
\(m_2 = \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1}\)
(3) Menentukan hubungan antara \(m_1\) dan \(m_2\)
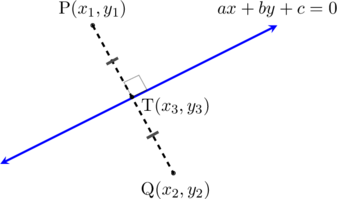
Karena garis \(ax + by + c = 0\) dan garis PQ saling tegak lurus maka berlaku:
\(\color {blue} m_1 \times m_2 = -1\)
\(-\dfrac{a}{b} \times \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1} = -1\)
\(\dfrac{ay_2\:-\:ay_1}{bx_2\:-\:bx_1} = 1\dotso\color{blue} (1)\)
(4) Menentukan koordinat titik T
Titik T adalah titik potong antara garis \(ax + by + c = 0\) dan garis PQ
Titik T juga merupakan titik tengah ruas garis PQ
\(\text{T} (x_3, y_3) = \left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
Titik T juga dilalui oleh garis \(ax + by + c = 0\)
\(ax_3 + by_3 + c = 0\)
\(a\left(\dfrac{x_1 + x_2}{2}\right) + b\left(\dfrac{y_1 + y_2}{2}\right) + c = 0\dotso\color{blue} (2)\)
(5) Menentukan koordinat titik Q
Koordinat titik \(\text{Q} (x_2, y_2)\) didapatkan dengan cara eliminasi atau substitusi persamaan (1) dan (2)
CONTOH SOAL
Tentukan bayangan titik P(0, 4) ke garis \(-4x + 2y + 1 = 0\)
Penyelesaian:
(1) Menentukan gradien garis \(-4x + 2y + 1 = 0\)
\(2y = 4x \:-\: 1\)
\(y = \frac{4}{2}x \:-\: \frac{1}{2}\)
\(y = 2x \:-\: \frac{1}{2}\)
Gradien garis \(m_1\) = 2
(2) Menentukan gradien garis yang melalui titik P dan Q
Misalkan bayangan titik \(\text{P}(0, 4)\) adalah \(\text{Q}(x_2, y_2)\)
Gradien garis yang melalui titik \(\text{P}(0, 4)\)dan\(\text{Q}(x_2, y_2)\) adalah:
\(m_2 = \dfrac{y_2\:-\:4}{x_2\:-\:0}\)
\(m_2 = \dfrac{y_2\:-\:4}{x_2}\)
(3) Menentukan hubungan antara \(m_1\) dan \(m_2\)
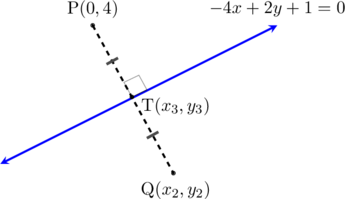
Karena garis \(-4x + 2y + 1 = 0\) dan garis PQ saling tegak lurus maka berlaku:
\(\color {blue} m_1 \times m_2 = -1\)
\(2\times \dfrac{y_2\:-\:4}{x_2} = -1\)
\(\dfrac{2y_2\:-\:8}{x_2} = 1\dotso\color{blue} (1)\)
(4) Menentukan koordinat titik T
Titik T adalah titik potong antara garis \(-4x + 2y + 1 = 0\) dan garis PQ
Titik T juga merupakan titik tengah ruas garis PQ
\(\text{T} (x_3, y_3) = \left(\dfrac{0 + x_2}{2}, \dfrac{4 + y_2}{2}\right)\)
Titik T juga dilalui oleh garis \(-4x + 2y + 1 = 0\)
\(-4x_3 + 2y_3 + 1 = 0\)
\(-4\left(\dfrac{0 + x_2}{2}\right) + 2\left(\dfrac{4 + y_2}{2}\right) + 1 = 0\)
\(-2x_2 + 4 + y_2 + 1 = 0\)
\(-2x_2 + y_2 = -5\)
\(y_2 = 2x_2 \:-\:5\dotso\color{blue} (2)\)
(5) Menentukan koordinat titik Q
Koordinat titik \(\text{Q} (x_2, y_2)\) didapatkan dengan cara substitusi persamaan (2) ke persamaan (1)
\(y_2 = 2x_2 \:-\:5\dotso\color{blue} (2)\)
\(\dfrac{2y_2\:-\:8}{x_2} = 1\dotso\color{blue} (1)\)
\(\dfrac{2(2x_2 \:-\:5)\:-\:8}{x_2} = 1\)
\(\dfrac{4x_2 \:-\:10\:-\:8}{x_2} = 1\)
\(4x_2 \:-\:18 = x_2\)
\(4x_2\:-\:x_2 = 18\)
\(3x_2 = 18\)
\(x_2 = 6\)
\(y_2 = 2(6) \:-\:5\)
\(y_2 = 12 \:-\:5\)
\(y_2 = 7\)
Koordinat titik Q adalah (6, 7)
Jadi, bayangan titik P(0, 4) ke garis \(-4x + 2y + 1 = 0\) adalah Q(6, 7)
