A. Rumus Dasar Tekanan
Tekanan adalah gaya yang dikerjakan per satuan luas bidang tekan.
\(\color{blue} \text{P} = \dfrac{\text{F}}{\text{A}}\)
\(\text{P}\) = tekanan (N/m²)
\(\text{F}\) = gaya tekan (N)
\(\text{A}\) = luas bidang tekan (m²)
Contoh soal:
Sebuah balok bermassa 400 gram diletakkan di atas lantai. (g = 10 m/s²)
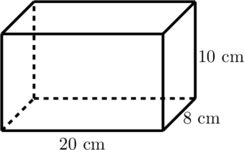
Tentukan tekanan maksimum dan tekanan minimum yang diakibatkan oleh balok pada permukaan lantai tersebut.
Penyelesaian:
Menentukan tekanan maksimum yang diakibatkan balok
Agar tekanan maksimum maka luas permukaan balok yang menekan lantai harus minimum
\(\text{A}_{\text{min}} = 0,08 \text{ m } \times 0,10 \text{ m }\)
\(\text{A}_{\text{min}} = 8 \times 10^{-3} \text{ m}^2\)
\(\text{F} = \text{ gaya berat} = m \cdot g\)
\(\text{F} = \text{ gaya berat} = 0,4 \text{ kg} \cdot 10 \text{ m/s²}\)
\(\text{F} = \text{ gaya berat} = 4 \text{ N}\)
\(\text{P}_{\text{max}} = \dfrac{\text{F}}{\text{A}_{\text{min}}}\)
\(\text{P}_{\text{max}} = \dfrac{4}{8 \times 10^{-3}}\)
\(\text{P}_{\text{max}} = 500 \text{ N/m²}\)
Menentukan tekanan minimum yang diakibatkan balok
Agar tekanan minimum maka luas permukaan balok yang menekan lantai harus maksimum
\(\text{A}_{\text{max}} = 0,20 \text{ m } \times 0,10 \text{ m }\)
\(\text{A}_{\text{max}} = 2 \times 10^{-2} \text{ m}^2\)
\(\text{F} = \text{ gaya berat} = m \cdot g\)
\(\text{F} = \text{ gaya berat} = 0,4 \text{ kg} \cdot 10 \text{ m/s²}\)
\(\text{F} = \text{ gaya berat} = 4 \text{ N}\)
\(\text{P}_{\text{min}} = \dfrac{\text{F}}{\text{A}_{\text{max}}}\)
\(\text{P}_{\text{min}} = \dfrac{4}{2 \times 10^{-2}}\)
\(\text{P}_{\text{min}} = 200 \text{ N/m²}\)
B. Tekanan Hidrostatis
Tekanan hidrostatis adalah tekanan yang diberikan oleh suatu fluida yang berada dalam kesetimbangan (statis) ke segala arah pada suatu benda.
\(\color{blue} \text{P}_{\text{h}} = \rho_{\text{fluida}} \cdot g \cdot h\)
\(\text{P}_{\text{h}}\) = tekanan hidrostatis (Pa atau N/m²)
\(\rho_{\text{fluida}}\) = massa jenis fluida (kg/m³)
\(g\) = percepatan gravitasi (m/s²)
\(h\) = kedalaman (m}
Contoh 1
Tentukan tekanan hidrostatis yang dirasakan oleh seorang penyelam yang berada pada kedalaman 20 meter di bawah permukaan air laut.
(g = 10 m/s², massa jenis air laut ρ = 1,02 g/cm³)
Penyelesaian:
\(\text{P}_{\text{h}} = \rho_{\text{fluida}} \cdot g \cdot h\)
massa jenis air laut ρ = 1,02 g/cm³ = 1020 kg/m³
\(\text{P}_{\text{h}} = 1020 \cdot 10 \cdot 20\)
\(\text{P}_{\text{h}} = 204.000 \text{ Pa}\)
\(\text{P}_{\text{h}} = 204 \text{ kPa}\)
Contoh 2
Tentukan tekanan mutlak (tekanan total) yang dirasakan oleh seorang penyelam yang berada pada kedalaman 20 meter di bawah permukaan air laut.
(g = 10 m/s², massa jenis air laut ρ = 1,02 g/cm³, tekanan udara di permukaan air laut = \(1 \times 10^5\) Pa)
Penyelesaian:
Untuk menghitung tekanan mutlak yang dirasakan oleh seorang penyelam yang berada pada kedalaman 20 meter di bawah permukaan air laut adalah dengan cara menjumlahkan antara tekanan hidrostatis dan tekanan udara di permukaan air laut.
\(\text{P}_{\text{mutlak}} = \text{P}_{\text{h}} + \text{P}_{\text{0}} \)
\(\text{P}_{\text{mutlak}} = \rho_{\text{fluida}} \cdot g \cdot h + 1 \times 10^5 \)
\(\text{P}_{\text{mutlak}} = 1020 \cdot 10 \cdot 20 + 1 \times 10^5 \)
\(\text{P}_{\text{mutlak}} = 204.000 + 100.000 \)
\(\text{P}_{\text{mutlak}} = 304.000 \text{ Pa}\)
\(\text{P}_{\text{mutlak}} = 304 \text{ kPa}\)
