Diketahui kubus ABCD.EFGH. P titik tengah CG, O pusat ABCD. Bila \(\theta\) adalah sudut antara bidang PBD dan bidang BDE. Hitunglah \(\cos \theta\)
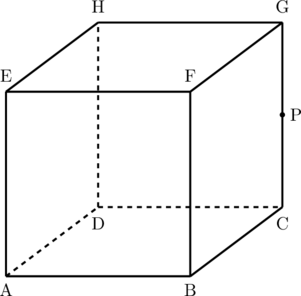
Pembahasan:
Langkah 1: Gambar bidang PBD dan bidang BDE
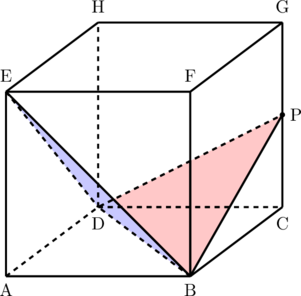
Langkah 2: Buat bidang yang memotong PBD dan BDE secara tegak lurus.
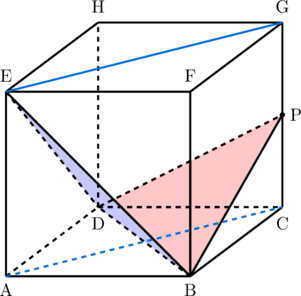
Bidang tersebut adalah ACGE
Langkah 3: Tentukan garis potong antara bidang ACGE dengan bidang PBD dan bidang BDE.
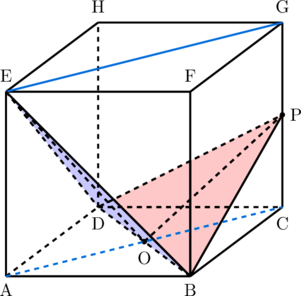
Garis potong antara bidang ACGE dan BDE adalah OE
Garis potong antara bidang ACGE dan PBD adalah OP
Langkah 4: Menentukan sudut yang dibentuk oleh garis OE dan OP
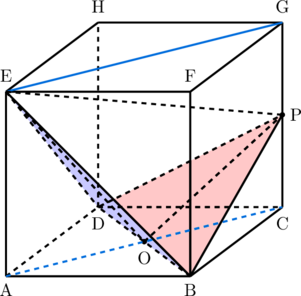
Lihat segitiga EOP,
Misal sudut yang dibentuk oleh garis OE dan OP adalah θ
Gunakan aturan cosinus untuk menghitung cos θ
\(\text{EP}^2 = \text{EO}^2 + \text{OP}^2 \:-\:2\cdot \text{EO}\cdot \text{OP}\cdot \cos \theta\)
\(\left(\dfrac{3}{2}\right)^2 = \left(\dfrac{1}{2}\sqrt{6}\right)^2 + \left(\dfrac{1}{2}\sqrt{3}\right)^2\:-\:2\cdot \dfrac{1}{2}\sqrt{6} \cdot \dfrac{1}{2}\sqrt{3} \cdot \cos \theta\)
\(\dfrac{9}{4} = \dfrac{6}{4} + \dfrac{3}{4}\:-\:\cancel{2}\cdot \dfrac{1}{\cancel{2}}\sqrt{6} \cdot \dfrac{1}{2}\sqrt{3} \cdot \cos \theta\)
\(\dfrac{9}{4} \:-\: \dfrac{6}{4} \:-\: \dfrac{3}{4}=- \dfrac{1}{2}\sqrt{18} \cdot \cos \theta\)
\(0 =- \dfrac{1}{2}\sqrt{18} \cdot \cos \theta\)
\(\cos \theta = 0\)
