Misal titik \(\text{M}(x_1, y_1)\) berada di luar lingkaran. Langkah-langkah menentukan persamaan garis singgung lingkaran yang ditarik dari titik M adalah sebagai berikut:
Langkah 1: Menentukan Persamaan Garis Polar
Garis polar adalah garis yang melalui kedua titik singgung lingkaran (lihat gambar di bawah ini)
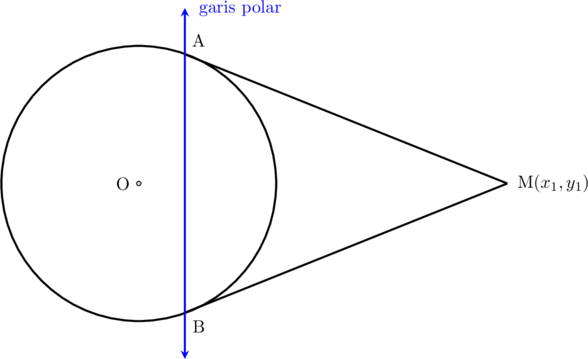
Persamaan garis polar dari titik \((x_1, y_1)\) yang terletak di luar lingkaran adalah sebagai berikut:
| Persamaan Lingkaran | Persamaan Garis Polar |
| \(x^2 + y^2 = r^2\) | \(x_1\cdot x + y_1 \cdot y = r^2\) |
| \((x\:-\:a)^2 + (y\:-\:b)^2 = r^2\) | \((x_1 \:-\:a)(x\:-\:a) + (y_1\:-\:b)(y\:-\:b) = r^2\) |
| \(x^2 + y^2 + Ax + By + C = 0\) | \(x_1\cdot x + y_1 \cdot y + \dfrac{1}{2}A(x + x_1) + \dfrac{1}{2}B(y + y_1) + C = 0\) |
Langkah 2: Menentukan Titik-Titik Singgung
Titik-titik singgung pada lingkaran dapat ditemukan dengan cara mensubstitusikan persamaan garis polar ke dalam persamaan lingkaran.
Langkah 3: Menentukan Persamaan Garis Singgung
Persamaan garis singgung lingkaran yang melalui titik singgung \((x_1, y_1)\) adalah sebagai berikut:
| Persamaan Lingkaran | Persamaan Garis Singgung |
| \(x^2 + y^2 = r^2\) | \(x_1\cdot x + y_1 \cdot y = r^2\) |
| \((x\:-\:a)^2 + (y\:-\:b)^2 = r^2\) | \((x_1 \:-\:a)(x\:-\:a) + (y_1\:-\:b)(y\:-\:b) = r^2\) |
| \(x^2 + y^2 + Ax + By + C = 0\) | \(x_1\cdot x + y_1 \cdot y + \dfrac{1}{2}A(x + x_1) + \dfrac{1}{2}B(y + y_1) + C = 0\) |
Panjang Garis Singgung
Panjang garis singgung yang ditarik dari titik \(\text{M}(x, y)\) di luar lingkaran ke titik singgung lingkaran adalah:
\(\color{blue} \sqrt{\text{K}}\)
dengan \(\text{K}\) adalah kuasa titik terhadap lingkaran
CONTOH SOAL
Contoh 1
Tentukan persamaan garis polar dari masing-masing lingkaran berikut:
(A) \(x^2 + y^2 = 11\) di titik \((3, -5)\)
(B) \((x + 3)^2 + (y\:-\:4)^2 = 10\) di titik \((7, 0)\)
(C) \(x^2 + y^2 + 10x \:-\: 2y \:-\:16 = 0\) di titik \((5, 8)\)
Contoh 2
Tentukan persamaan garis singgung lingkaran \(x^2 + y^2 = 13\) yang ditarik dari titik \(\text{M}(-5, 1)\)