PERSAMAAN GARIS
$$\bbox[yellow, 5px, border: 2px solid red] {y = mx + c}$$
Keterangan:
\(m = \text{ gradien/ukuran kemiringan garis} = \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1}\)
\(c = \text{ konstanta}\)
A. Menggambar Garis
Untuk dapat menggambar garis minimal diketahui 2 titik yang dilalui.
Contoh 01
Gambarkan garis \(y = 2x\:-\:8\)
Penyelesaian:
Ambil \(x_1 = 0\) maka \(y_1 = 2(0)\:-\:8 = -8\)
\(\color{red}(0, -8)\)
Ambil \(y_2 = 0\) maka \(0 = 2x_2\:-\:8 \rightarrow x_2 = 4\)
\(\color{red}(4, 0)\)
Tarik garis lurus melewati titik \((0, -8)\) dan \((4, 0)\), diperoleh gambar sebagai berikut:
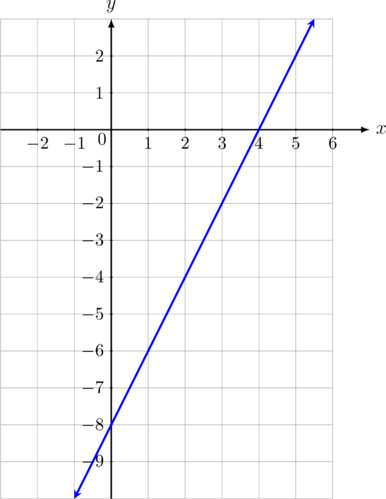
Contoh 02
Gambarkan garis \(y = 4\)
Penyelesaian:
Garis \(y = 4\) adalah garis horizontal yang melalui titik \((0, 4)\)
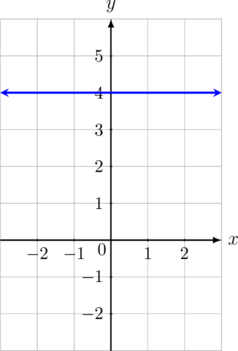
Contoh 03
Gambarkan garis \(x = 4\)
Penyelesaian:
Garis \(x = 4\) adalah garis vertikal yang melalui titik \((4, 0)\)
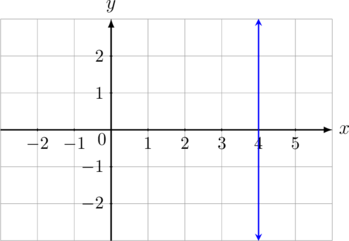
Contoh 04
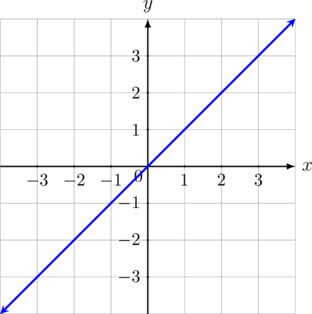
Gambarkan garis \(y = x\)
Penyelesaian:
Garis \(y = x\) melalui titik asal \((0, 0)\) dan melalui titik-titik dengan nilai absis = ordinat seperti \((-1, -1), (1, 1), (2, 2), (3, 3)\)
B. Menentukan Persamaan Garis
(1) Diketahui gradien dan satu titik yang dilalui
Persamaan garis dengan gradien \(m\) dan melalui titik \((x_1, y_1)\) adalah:
$$\bbox[yellow, 5px, border: 2px solid red] {y\:-\:y_1 = m(x\:-\:x_1)}$$
Contoh:
Tentukan persamaan garis bergradien \(-2\) dan melalui titik \((-1, 5)\).
Penyelesaian:
\(y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:5 = -2(x\:-\:(-1))\)
\(y\:-\:5 = 2x \:-\:2\)
\(y = 2x + 3\)
atau dapat ditulis:
\(y\:-\:2x\:-\:3 = 0\)
(2) Diketahui dua buah titik yang dilalui
Persamaan garis melalui titik \((x_1, y_1)\) dan \((x_2, y_2)\)
$$\bbox[yellow, 5px, border: 2px solid red] {\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}}$$
Contoh:
Tentukan persamaan garis melalui titik \((0, -3)\) dan \((4, -1)\).
Penyelesaian:
Cara 1
\(\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}\)
\(\dfrac{y\:-\:(-3)}{-1\:-\:(-3)} = \dfrac{x\:-\:0}{4\:-\:0}\)
\(\dfrac{y + 3}{2} = \dfrac{x}{4}\)
kali silang,
\(4(y + 3) = 2x\)
\(4y + 12 = 2x\)
\(4y\:-\:2x + 12 = 0\) bagi kedua ruas dengan 2
\(2y\:-\:x + 6= 0\)
Cara 2
Menentukan gradien garis \(m\)
\(m = \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1}\)
\(m = \dfrac{-1\:-\:(-3)}{4\:-\:0}\)
\(m = \dfrac{2}{4} = \dfrac{1}{2}\)
Persamaan garis \(y = mx + c\)
\(y = \dfrac{1}{2}x + c\)
kemudian substitusikan salah satu titik yang dilalui untuk menentukan konstanta \(c\)
Pilih \((0, -3)\)
\(-3= \dfrac{1}{2}(0) + c\)
\(c = -3\)
Persamaan garisnya adalah \(y = \dfrac{1}{2}x \:-\:3\) atau dapat ditulis \(2y\:-\:x + 6= 0\)
