Soal 01
Persamaan garis \(2y\:-\:6x + 1 = 0\) memiliki gradien…
(A) 1
(B) 2
(C) 3
(D) 4
Jawaban: C
Ubah persamaan garis menjadi bentuk \(y = mx + c\) dengan \(m\) adalah gradien(kemiringan) garis.
\(2y\:-\:6x + 1 = 0\)
\(2y = 6x \:-\:1\)
\(y = 3x \:-\:\dfrac{1}{2}\)
Gradien garis \(m = 3\)
Soal 02
Garis yang melalui titik \((3, 5)\) dan \((2, 1)\) memiliki gradien…
(A) 2
(B) 3
(C) 4
(D) 6
Jawaban: C
\(\color{blue} m = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\((x_1, y_1) = (3, 5)\) dan \((x_2, y_2) = (2, 1)\)
\(m = \dfrac{1\:-\:5}{2 \:-\:3}\)
\(m = \dfrac{-4}{-1}\)
\(m = 4\)
Soal 03
Garis \(y = 2x + 4\) akan melalui titik…
(A) \((2, 3)\)
(B) \((-1, 4)\)
(C) \((0, -4)\)
(D) \((-3, -2)\)
Jawaban: D
Garis \(y = 2x + 4\) akan melalui titik \((-3, -2)\), karena
\(-2 = 2(-3) + 4\)
\(-2 = -6 + 4\)
\(-2 = -2\) (membentuk kesamaan nilai)
Soal 04
Jika garis \(4x + y + c = 0\) melalui titik \((-4, 12)\), maka nilai \(c\) yang memenuhi adalah…
(A) \(-2\)
(B) 3
(C) 4
(D) 5
Jawaban: C
Garis \(4x + y + c = 0\) melalui titik \((-4, 12)\)
\(4(-4) + 12 + c = 0\)
\(-16 + 12 + c = 0\)
\(-4 + c = 0\)
\(c = 4\)
Soal 05
Garis \(2x + y \:-\:8 = 0\) memotong sumbu X di titik berabsis \(m\) dan memotong sumbu Y di titik berordinat \(n\), maka nilai \(m + n = \dotso\)
(A) 10
(B) 12
(C) 14
(D) 16
Jawaban: B
Garis \(2x + y \:-\:8 = 0\) memotong sumbu X, jika \(y = 0\)
\(2x + 0 \:-\: 8 = 0\)
\(2x = 8\)
\(x = \dfrac{8}{2} = 4\)
\(m = 4\)
Garis \(2x + y \:-\:8 = 0\) memotong sumbu Y, jika \(x = 0\)
\(2(0) + y \:-\:8 = 0\)
\(y = 8\)
\(n = 8\)
\(m + n = 4 + 8\)
\(m + n = 12\)
Soal 06
Persamaan garis yang melalui titik \((2, 3)\) dan bergradien \(m = -5\) adalah…
(A) \(y = -4x + 13\)
(B) \(y = -5x + 13\)
(C) \(y = -5x + 15\)
(D) \(y = -6x + 11\)
Jawaban: B
Persamaan garis yang melalui titik \((2, 3)\) dan bergradien \(m = -5\) adalah \(y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:3 = -5(x\:-\:2)\)
\(y\:-\:3 = -5x + 10\)
\(y = -5x + 10 + 3\)
\(y = -5x + 13\)
Soal 07
Persamaan garis yang melalui titik \((0, -4)\) dan \((-2, 8)\) adalah…
(A) \(y = -6x\:-\:4\)
(B) \(y = -3x\:-\:4\)
(C) \(y = -4x\:-\:4\)
(D) \(y = -5x\:-\:2\)
Jawaban: A
Cara 1:
Persamaan garis yang melalui dua buah titik:
\(\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2 \:-\:x_1}\)
\((x_1, y_1) =(0, -4)\) dan \((x_2, y_2) = (-2, 8)\)
\(\dfrac{y\:-\:(-4)}{8\:-\:(-4)} = \dfrac{x\:-\:0}{-2 \:-\:0}\)
\(\dfrac{y + 4}{12} = \dfrac{x}{-2}\)
Kali silang,
\(-2(y + 4) = 12x\)
\(-2y \:-\:8 = 12x\)
Bagi kedua ruas dengan \(-2\)
\(y + 4 = -6x\)
\(y = -6x\:-\:4\)
Cara 2:
Persamaan garis \(y = mx + c\)
\(m = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1} = \dfrac{8\:-\:(-4)}{-2\: – \:0}\)
\(m = \dfrac{12}{-2}\)
\(m = -6\)
Persamaan garis \(y = -6x + c\) melalui titik \((0, -4)\)
\(-4 = -6(0) + c\)
\(c = -4\)
Jadi persamaan garisnya adalah \(y = -6x\:-\:4\)
Soal 08
Persamaan garis yang melalui titik \((2, -6)\) dan sejajar dengan garis \(4x + y + 15 = 0\) adalah…
(A) \(y = -x + 1\)
(B) \(y = -2x + 2\)
(C) \(y = -4x \:-\: 2\)
(D) \(y = -4x + 2\)
Jawaban: D
Langkah 1: Menentukan gradien garis \(4x + y + 15 = 0\)
\(y = -4x \:-\:15\)
\(m_1 = -4\)
Langkah 2: Menentukan gradien garis yang dicari yaitu \(m_2\)
Karena garis \(4x + y + 15 = 0\) dan garis dicari saling sejajar, maka \(m_1 = m_2\)
\(m_2 = m_1 = -4\)
Langkah 3: Menentukan persamaan garis yang melalui titik \((2, -6)\) dan bergradien \(-4\)
\(y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:(-6) = -4(x\:-\:2)\)
\(y + 6 = -4x + 8\)
\(y = -4x + 8\:-\:6\)
\(y = -4x + 2\)
Soal 09
Perhatikan gambar berikut:
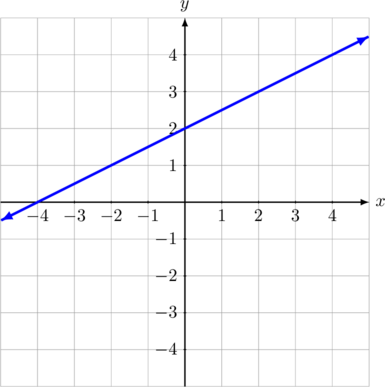
Persamaan garis di atas adalah…
(A) \(2y\:-\:x + 2 = 0\)
(B) \(y\:-\:x\:-\:4 = 0\)
(C) \(2y\:-\:x\:-\:4 = 0\)
(D) \(2y\:-\:x\:-\:5 = 0\)
Jawaban: C
Garis di atas melewati titik \((0, 2)\) dan juga \((2, 3)\)
Persamaan garis melalui dua titik tersebut adalah:
\(\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2 \:-\:x_1}\)
\(\dfrac{y\:-\:2}{3\:-\:2} = \dfrac{x\:-\:0}{2 \:-\:0}\)
\(\dfrac{y\:-\:2}{1} = \dfrac{x}{2}\)
Kali silang,
\(2(y\:-\:2) = x\)
\(2y\:-\:4 = x\)
\(2y\:-\:x\:-\:4 = 0\)
Soal 10
Perhatikan gambar berikut:
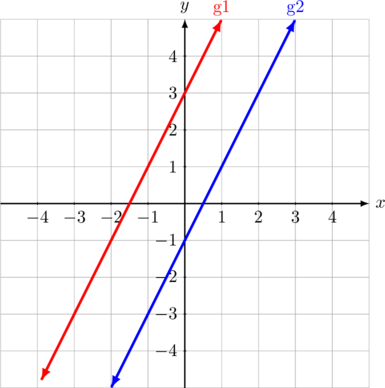
Pernyataan yang benar tentang kedua garis di atas adalah…
(A) Kedua garis tersebut saling tegak lurus
(B) Persamaan garis pertama (warna merah) adalah \(2y\:-\:x + 10 = 0\)
(C) Persamaan garis kedua (warna biru) adalah \(y\:-\:2x + 1 = 0\)
(D) Garis pertama memotong sumbu Y di titik \((3, 0)\)
Jawaban: C
Garis pertama (warna merah) melalui titik \((0, 3)\) dan \((-3, -3)\), persamaan garis pertama adalah:
\(\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2 \:-\:x_1}\)
\(\dfrac{y\:-\:3}{-3\:-\:3} = \dfrac{x\:-\:0}{-3 \:-\:0}\)
\(\dfrac{y\:-\:3}{-6} = \dfrac{x}{-3}\)
Kali silang,
\(-3(y\:-\:3) = -6x\)
\(-3y + 9 = -6x\)
Bagi kedua ruas dengan \(-3\)
\(y\:-\:3 = 2x\)
\(y\:-\:2x \:-\:3 = 0\)
Garis kedua (warna biru) melalui titik \((1, 1)\) dan \((2, 3)\), persamaan garis kedua adalah:
\(\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2 \:-\:x_1}\)
\(\dfrac{y\:-\:1}{3\:-\:1} = \dfrac{x\:-\:1}{2 \:-\:1}\)
\(\dfrac{y\:-\:1}{2} = \dfrac{x\:-\:1}{1}\)
Kali silang,
\(y\:-\:1 = 2(x\:-\:1)\)
\(y\:-\:1 = 2x \:-\:2\)
\(y\:-\:2x + 1 = 0\)
Garis pertama dan kedua saling sejajar karena memiliki gradien yang sama.
