SOAL 1
Tentukan luas daerah yang diarsir berikut:
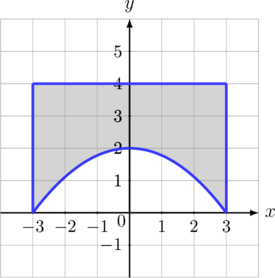
Luas daerah yang diarsir dapat dihitung dengan mengurangi luas persegi panjang dengan luas daerah yang dibatasi parabola dengan sumbu \(x\)
karena fungsi parabola belum diketahui maka kita cari persamaan fungsinya terlebih dahulu
Parabola memotong sumbu \(x\) di titik (−3, 0) dan (3, 0) sehingga \(x_1 = -3 \text{ dan } x_2 = 3\)
Persamaan parabola:
\(y = a(x \:-\: x_1)(x \:-\: x_2)\)
\(y = a(x +3)(x \:-\: 3)\)
Selanjutnya mencari nilai \(a\) dengan substitusi titik lain yang terletak pada parabola, yaitu (0, 2)
\(2 = a(0 +3)(0 – 3)\)
\(2 = a(-9)\)
\(a = -\frac{2}{9}\)
Jadi persamaan parabolanya adalah \(y = -\frac{2}{9}(x +3)(x\:-\: 3)\) atau \(y = -\frac{2}{9}x^2 + 2\)
Luas daerah yang diarsir = \((6 \times 4) \:-\: \int_{-3}^{3}(-\frac{2}{9}x^2 + 2) \text{ dx}\)
Luas daerah yang diarsir = \(24 \:-\: \left.(-\frac{2}{27}x^3 + 2x) \right |_{-3}^{3}\)
Luas daerah yang diarsir = 24 – [4 – (-4)]
Luas daerah yang diarsir = 24 – 8 = 16 satuan luas
