SOAL 01
Tentukan luas daerah yang diarsir berikut:
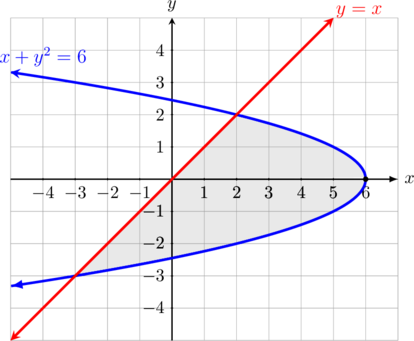
Langkah 1: Menentukan titik potong kedua grafik
Substitusikan \(y = x\) ke dalam persamaan \( x + y^2 = 6\)
\(x + x^2 = 6\)
\(x^2 + x – 6 = 0\:\:\:\:\:\color{blue}\text{faktorkan}\)
\((x + 3)(x – 2) = 0\)
\(x_1 = -3 \rightarrow y_1 = -3\)
\(x_2 = 2 \rightarrow y_1 = 2\)
Jadi titik potong kedua grafik berada di koordinat \((-3, -3)\) dan \((2, 2)\)
Langkah 2: Menentukan luas
persamaan \(y=x\) kita ubah menjadi bentuk \( x= y\) sehingga \(g(y) = y\)
Persamaan kurva \( x + y^2 = 6\) kita ubah menjadi bentuk \( x = 6 – y^2\) sehingga \(f(y) = 6 – y^2\)
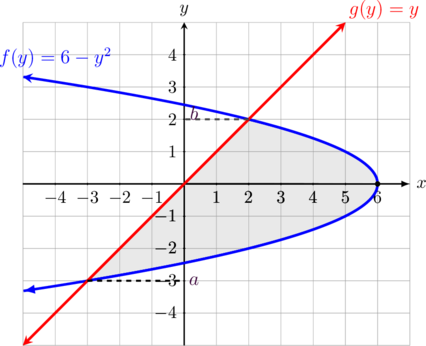
Untuk menghitung luas kita gunakan batas integral terhadap sumbu y dari \(a\) sampai \(b\) untuk fungsi sebelah kanan \(f(y) = 6 – y^2\) dikurangi fungsi sebelah kiri \(g(y) = y\) pada daerah yang diarsir.
\(\text{Luas daerah yang diarsir} = \int_{a}^{b} (f(y) – g(y)) \text{ dy}\)
\(\int_{-3}^{2} (6 \:-\: y^2\:-\:y) \text{ dy}\)
\(\int_{-3}^{2} (-y^2 \:-\: y + 6) \text{ dy}\)
\(\left.(-\frac{1}{3}y^3\: -\: \frac{1}{2}y^2 + 6y)\right |_{-3}^2\)
\((-\frac{1}{3}(2)^3 \:-\: \frac{1}{2}(2)^2 + 6(2)) \:-\: (-\frac{1}{3}(-3)^3 – \frac{1}{2}(-3)^2 + 6(-3))\)
\((-\frac{8}{3} – 2 + 12) \:-\: (9 \:-\: \frac{9}{2} -18) \)
\(-\frac{8}{3} + \frac{9}{2} + 19\)
\(\frac{125}{6}\text{ satuan luas}\)
Jadi luas daerah yang diarsir adalah \(\frac{125}{6}\text{ satuan luas}\)
