Diagram Venn digunakan untuk menggambarkan semua kemungkinan hubungan dari himpunan yang berbeda.
Dalam diagram Venn terdapat himpunan semesta dan himpunan-himpunan lainnya yang berada di dalamnya.
Himpunan semesta biasanya digambarkan dengan bentuk persegi panjang sedangkan himpunan-himpunan yang berada di dalamnya digambarkan dengan bentuk lingkaran.
Gambarkan diagram Venn yang memuat himpunan semesta \(\color{blue} \textbf{S} \color{black}= \lbrace 1, 2, 3, 4, 5, 6, 7, 8 \rbrace\), himpunan \(\textbf{A} = \lbrace 2, 3, 5 \rbrace\), dan himpunan \(\textbf{B} = \lbrace 5, 7, 8 \rbrace\).
(4) Gabungan dari himpunan A dan B \(\:\:\color{red}(\textbf{A} \cup \textbf{B})\)
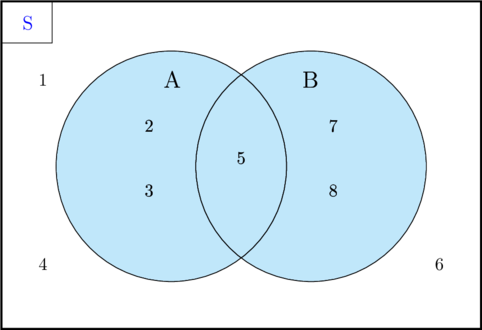
(1) Menentukan komplemen dari himpunan A \(\:\:\color{red}(\textbf{A}^c)\)
Komplemen dari himpunan A adalah semua anggota himpunan semesta yang bukan anggota himpunan A.
\(\:\:\color{red}(\textbf{A}^c) = \lbrace 1, 4, 6, 7, 8 \rbrace\)
(2) Menentukan komplemen dari himpunan B\(\:\:\color{red}(\textbf{B}^c)\)
Komplemen dari himpunan B adalah semua anggota himpunan semesta yang bukan anggota himpunan B.
\(\:\:\color{red}(\textbf{B}^c) = \lbrace 1, 2, 3, 4, 6 \rbrace\)
(3) Menentukan irisan dari himpunan A dan B \(\:\:\color{red}(\textbf{A} \cap \textbf{B})\)
Irisan dari himpunan A dan B adalah himpunan yang anggota-anggotanya ada di himpunan A dan ada di himpunan B.
\(\:\:\color{red}(\textbf{A} \cap \textbf{B}) = \lbrace 5 \rbrace\)
(4) Menentukan gabungan dari himpunan A dan B \(\:\:\color{red}(\textbf{A} \cup \textbf{B})\)
Gabungan dari himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan gabungan dari himpunan A dan himpunan B.
\(\:\:\color{red}(\textbf{A} \cup \textbf{B}) = \lbrace 2, 3, 5, 7, 8 \rbrace\)
Terdapat 32 siswa dalam satu kelas.
Dua belas siswa suka menggambar.
Dua puluh siswa suka menari.
Tiga orang siswa suka menggambar dan menari.
(1) Menggambar diagram Venn
Misal:
Semesta himpunannya adalah semua siswa di kelas tersebut.
\(n\textbf{(S)} = 32\)
A = himpunan siswa yang suka menggambar
\(n\textbf{(A)} = 12\)
B = himpunan siswa yang suka menari
\(n\textbf{(B)} = 20\)
Irisan himpunan A dan B
n\((\textbf{A} \cap \textbf{B}) = 3\)
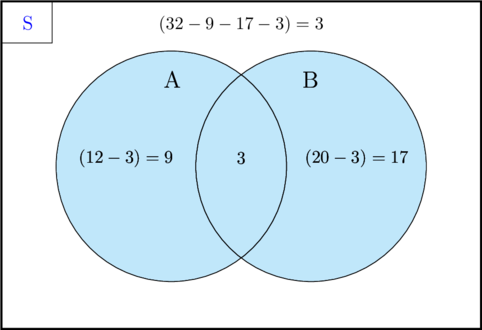
(2) Menentukan jumlah siswa yang hanya suka menggambar saja
Jumlah siswa yang hanya suka menggambar = jumlah siswa yang suka menggambar − jumlah siswa yang suka menggambar dan menari
\(n(\textbf{A} \:-\: \textbf{B}) = n(\textbf{A})\:-\:n(\textbf{A} \cap \textbf{B})\)
\(n(\textbf{A} \:-\: \textbf{B}) = 12 \:-\:3 = 9\)
Jadi, jumlah siswa yang hanya suka menggambar ada 9 orang
(3) Menentukan jumlah siswa yang hanya suka menari saja
Jumlah siswa yang hanya suka menari = jumlah siswa yang suka menari − jumlah siswa yang suka menggambar dan menari
\(n(\textbf{B} \:-\: \textbf{A}) = n(\textbf{B})\:-\:n(\textbf{A} \cap \textbf{B})\)
\(n(\textbf{B} \:-\: \textbf{A}) = 20 \:-\:3 = 17\)
Jadi, jumlah siswa yang hanya suka menari ada 17 orang
(4) Menentukan jumlah siswa yang suka menggambar atau menari
Jumlah siswa yang suka menggambar atau menari = jumlah siswa yang suka menggambar + jumlah siswa yang suka menari − jumlah siswa yang suka menggambar dan menari
\(n(\textbf{A} \cup \textbf{B}) = n(\textbf{A}) + n(\textbf{B})\:-\:n(\textbf{A} \cap \textbf{B})\)
\(n(\textbf{A} \cup \textbf{B}) = 12 + 20\:-\:3\)
\(n(\textbf{A} \cup \textbf{B}) = 29\)
Jadi, jumlah siswa yang suka menggambar atau menari ada 29 orang
(5) Menentukan jumlah siswa yang tidak suka keduanya
Jumlah siswa yang tidak suka keduanya = jumlah seluruh siswa − jumlah siswa yang suka menggambar atau menari.
\(n(\textbf{A} \cup\textbf{B})^c = n(\textbf{S})\:-\:n(\textbf{A} \cup \textbf{B})\)
\(n(\textbf{A} \cup\textbf{B})^c = 32 \:-\: 29\)
Jadi, jumlah siswa yang tidak suka menggambar maupun menari ada 3 orang
Terdapat 32 siswa dalam satu kelas.
Empat belas siswa menyukai warna merah.
Sepuluh siswa menyukai warna kuning.
Empat belas siswa menyukai warna hijau.
Empat siswa menyukai warna merah dan kuning.
Lima siswa menyukai warna hijau dan kuning.
Lima siswa menyukai warna merah dan hijau.
Tujuh siswa tidak menyukai ketiga warna tersebut.
Jumlah siswa yang senang ketiga warna tersebut \(x\) orang.
(1) Diagram Venn dari informasi tersebut.
(2) Jumlah siswa yang menyukai ketiga warna tersebut.
(3) Jumlah siswa yang hanya menyukai warna merah.
(4) Jumlah siswa yang hanya menyukai warna kuning.
(5) Jumlah siswa yang hanya menyukai warna hijau.
(6) Jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau.
(7) Jumlah siswa yang menyukai warna merah dan kuning tetapi tidak menyukai warna hijau.
(1) Menggambar diagram Venn
Misal:
Semesta himpunannya adalah semua siswa di kelas tersebut.
\(n\textbf{(S)} = 32\)
A = himpunan siswa yang menyukai warna merah
\(n\textbf{(A)} = 14\)
B = himpunan siswa yang menyukai warna kuning
\(n\textbf{(B)} = 10\)
C = himpunan siswa yang menyukai warna hijau
\(n\textbf{(C)} = 14\)
Irisan himpunan A, B, dan C
n\((\textbf{A} \cap \textbf{B} \cap \textbf{C}) = x\)
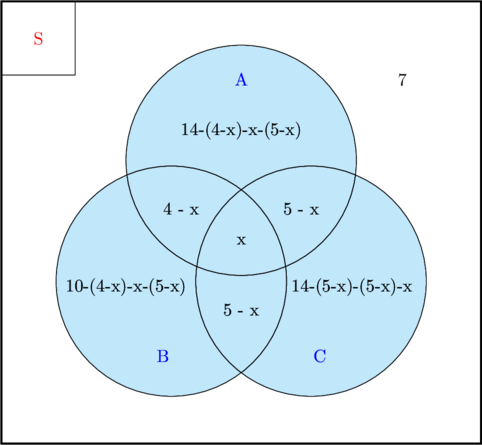
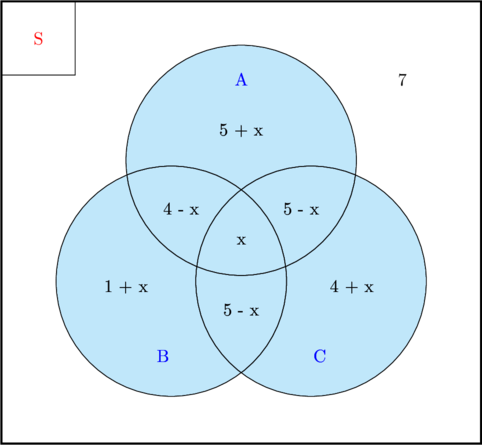
(2) Menentukan jumlah siswa yang menyukai ketiga warna tersebut.
(5 + x) + (4 − x) + x + (5 − x) + (1 + x) + (5 − x) + (4 + x) + 7 = 32
31 + x = 32
x = 32 − 31
x = 1
Jadi, jumlah siswa yang menyukai ketiga warna tersebut ada 1 orang.
(3) Menentukan jumlah siswa yang hanya menyukai warna merah.
Jumlah siswa yang hanya menyukai warna merah = 5 + x
Jumlah siswa yang hanya menyukai warna merah = 5 + 1 = 6
Jadi, jumlah siswa yang hanya menyukai warna merah ada 6 orang
(4) Menentukan jumlah siswa yang hanya menyukai warna kuning.
Jumlah siswa yang hanya menyukai warna kuning = 1 + x
Jumlah siswa yang hanya menyukai warna kuning = 1 + 1 = 2
Jadi, jumlah siswa yang hanya menyukai warna kuning ada 2 orang
(5) Menentukan jumlah siswa yang hanya menyukai warna hijau.
Jumlah siswa yang hanya menyukai warna hijau = 4 + x
Jumlah siswa yang hanya menyukai warna hijau = 4 + 1 = 5
Jadi, jumlah siswa yang hanya menyukai warna hijau ada 5 orang
(6) Menentukan jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau.
Jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau = (5 + x) + (4 − x) + (1 + x)
Jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau = 10 + x
Jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau = 10 + 1 = 11
Jadi, jumlah siswa yang menyukai warna merah atau kuning tetapi tidak menyukai warna hijau ada 11 orang.
(7) Menentukan jumlah siswa yang menyukai warna merah dan kuning tetapi tidak menyukai warna hijau.
Jumlah siswa yang menyukai warna merah dan kuning tetapi tidak menyukai warna hijau = 4 − x
Jumlah siswa yang menyukai warna merah dan kuning tetapi tidak menyukai warna hijau = 4 − 1 = 3
Jadi, jumlah siswa yang menyukai warna merah dan kuning tetapi tidak menyukai warna hijau ada 3 orang.
