Quiz-summary
0 of 15 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 30 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 15 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 15
1. Pertanyaan
1 pointsBerikut ini terdapat ukuran sisi-sisi dalam suatu segitiga.
(1) 3 cm, 4 cm, 5 cm
(2) 6 cm, 8 cm, 10 cm
(3) 5 cm, 12 cm, 13 cm
(4) 7 cm, 24 cm, 25 cm
(5) 8 cm, 10 cm, 12 cm
Yang bukan merupakan ukuran sisi dari segitiga siku-siku adalah pernyataan nomor…
Benar
Pada segitiga siku-siku berlaku rumus Pythagoras.
\(a^2 + b^2 = c^2\)
Dengan \(c\) adalah sisi miring (sisi terpanjang dalam segitiga siku-siku)
(1) \(3^2 + 4^2 = 5^2\:\:\color{blue} \text{benar}\)
(2) \(6^2 + 8^2 = 10^2\:\:\color{blue} \text{benar}\)
(3) \(5^2 + 12^2 = 13^2\:\:\color{blue} \text{benar}\)
(4) \(7^2 + 24^2 = 25^2\:\:\color{blue} \text{benar}\)
(5) \(8^2 + 10^2 \neq 12^2\:\:\color{blue} \text{salah}\)
Jadi, yang bukan merupakan ukuran sisi dalam segitiga siku-siku adalah pernyataan nomor 5.
Salah
Pada segitiga siku-siku berlaku rumus Pythagoras.
\(a^2 + b^2 = c^2\)
Dengan \(c\) adalah sisi miring (sisi terpanjang dalam segitiga siku-siku)
(1) \(3^2 + 4^2 = 5^2\:\:\color{blue} \text{benar}\)
(2) \(6^2 + 8^2 = 10^2\:\:\color{blue} \text{benar}\)
(3) \(5^2 + 12^2 = 13^2\:\:\color{blue} \text{benar}\)
(4) \(7^2 + 24^2 = 25^2\:\:\color{blue} \text{benar}\)
(5) \(8^2 + 10^2 \neq 12^2\:\:\color{blue} \text{salah}\)
Jadi, yang bukan merupakan ukuran sisi dalam segitiga siku-siku adalah pernyataan nomor 5.
-
Pertanyaan 2 dari 15
2. Pertanyaan
1 pointsTerdapat tiga buah persegi yang disusun seperti gambar di bawah ini.
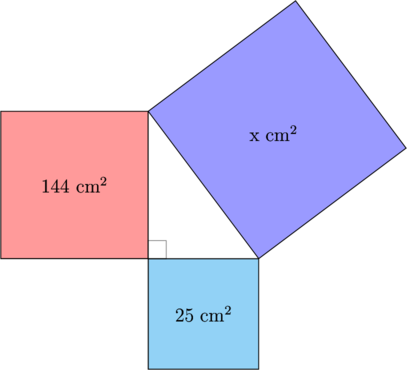
Nilai \(x = \dotso\)
Benar
\(x = 25 + 144 = 169\)
Salah
\(x = 25 + 144 = 169\)
-
Pertanyaan 3 dari 15
3. Pertanyaan
1 pointsPerhatikan segitiga siku-siku di bawah ini.
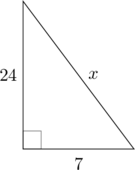
Nilai \(x = \dotso\)
Benar
\(7^2 + 24^2 = x^2\)
\(49 + 576 = x^2\)
\(x^2 = 625\)
\(x = \sqrt{625} = 25\)
Salah
\(7^2 + 24^2 = x^2\)
\(49 + 576 = x^2\)
\(x^2 = 625\)
\(x = \sqrt{625} = 25\)
-
Pertanyaan 4 dari 15
4. Pertanyaan
1 pointsPerhatikan segitiga siku-siku di bawah ini.
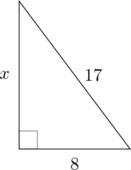
Nilai \(x = \dotso\)
Benar
\(x^2 + 8^2 = 17^2\)
\(x^2 + 64 = 289\)
\(x^2 = 289\:-\:64\)
\(x^2 = 225\)
\(x = \sqrt{225}\)
\(x = 15\)
Salah
\(x^2 + 8^2 = 17^2\)
\(x^2 + 64 = 289\)
\(x^2 = 289\:-\:64\)
\(x^2 = 225\)
\(x = \sqrt{225}\)
\(x = 15\)
-
Pertanyaan 5 dari 15
5. Pertanyaan
1 pointsPerhatikan segitiga siku-siku di bawah ini.
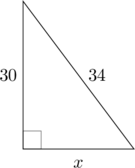
Nilai \(x = \dotso\)
Benar
\(x^2 + 30^2 = 34^2\)
\(x^2 + 900 = 1156\)
\(x^2 = 1156\:-\:900\)
\(x^2 = 256\)
\(x = \sqrt{256}\)
\(x = 16\)
Salah
\(x^2 + 30^2 = 34^2\)
\(x^2 + 900 = 1156\)
\(x^2 = 1156\:-\:900\)
\(x^2 = 256\)
\(x = \sqrt{256}\)
\(x = 16\)
-
Pertanyaan 6 dari 15
6. Pertanyaan
1 pointsPerhatikan segitiga siku-siku di bawah ini.
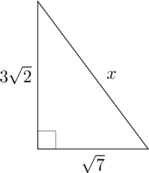
Nilai \(x = \dotso\)
Benar
\((\sqrt{7})^2 + (3\sqrt{2})^2 = x^2\)
\(7 + 18 = x^2\)
\(x^2 = 25\)
\(x = \sqrt{25}\)
\(x = 5\)
Salah
\((\sqrt{7})^2 + (3\sqrt{2})^2 = x^2\)
\(7 + 18 = x^2\)
\(x^2 = 25\)
\(x = \sqrt{25}\)
\(x = 5\)
-
Pertanyaan 7 dari 15
7. Pertanyaan
1 pointsPerhatikan segitiga siku-siku di bawah ini.
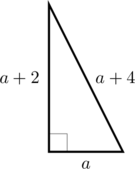
Nilai \(a = \dotso\)
Benar
\(a^2 + (a + 2)^2 = (a + 4)^2\)
Rumus penjabaran: \(\color{blue} (x + y)^2 = x^2 + 2xy + y^2\)
\(a^2 + a^2 + 4a + 4 = a^2 + 8a + 16\)
\(2a^2 \:-\:a^2+ 4a\:-\:8a + 4 \:-\:16 = 0\)
\(a^2 \:-\:4a \:-\:12 = 0\)
Faktorkan
\((a\:-\:6)(a + 2) = 0\)
\(a\:-\:6 = 0 \rightarrow a = 6\text{ memenuhi}\)
\(a + 2= 0 \rightarrow a = -2\color{red}\text{ TM}\)
Salah
\(a^2 + (a + 2)^2 = (a + 4)^2\)
Rumus penjabaran: \(\color{blue} (x + y)^2 = x^2 + 2xy + y^2\)
\(a^2 + a^2 + 4a + 4 = a^2 + 8a + 16\)
\(2a^2 \:-\:a^2+ 4a\:-\:8a + 4 \:-\:16 = 0\)
\(a^2 \:-\:4a \:-\:12 = 0\)
Faktorkan
\((a\:-\:6)(a + 2) = 0\)
\(a\:-\:6 = 0 \rightarrow a = 6\text{ memenuhi}\)
\(a + 2= 0 \rightarrow a = -2\color{red}\text{ TM}\)
-
Pertanyaan 8 dari 15
8. Pertanyaan
1 pointsPerhatikan balok ABCD.EFGH berikut ini.
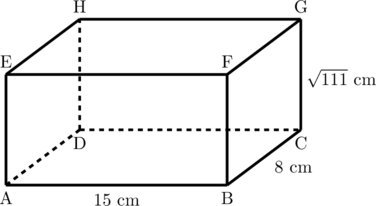
Panjang diagonal ruang \(\textbf{AG} = \dotso\)
Benar
Perhatikan segitiga siku-siku ABC untuk mencari panjang AC.
\(\text{AB}^2 + \text{BC}^2 = \text{AC}^2\)
\(15^2 + 8^2 = \text{AC}^2\)
\(225 + 64 = \text{AC}^2\)
\(\text{AC}^2 = 289\)
\(\text{AC} = \sqrt{289} = 17 \text{ cm}\)
Perhatikan segitiga siku-siku ACG
\(\text{AC}^2 + \text{CG}^2 = \text{AG}^2\)
\(17^2 + (\sqrt{111})^2 = \text{AG}^2\)
\(289 +111 = \text{AG}^2\)
\(\text{AG}^2 = 400\)
\(\text{AG} = \sqrt{400} = 20\text{ cm}\)
Salah
Perhatikan segitiga siku-siku ABC untuk mencari panjang AC.
\(\text{AB}^2 + \text{BC}^2 = \text{AC}^2\)
\(15^2 + 8^2 = \text{AC}^2\)
\(225 + 64 = \text{AC}^2\)
\(\text{AC}^2 = 289\)
\(\text{AC} = \sqrt{289} = 17 \text{ cm}\)
Perhatikan segitiga siku-siku ACG
\(\text{AC}^2 + \text{CG}^2 = \text{AG}^2\)
\(17^2 + (\sqrt{111})^2 = \text{AG}^2\)
\(289 +111 = \text{AG}^2\)
\(\text{AG}^2 = 400\)
\(\text{AG} = \sqrt{400} = 20\text{ cm}\)
-
Pertanyaan 9 dari 15
9. Pertanyaan
1 pointsPerhatikan belah ketupat ABCD berikut ini.
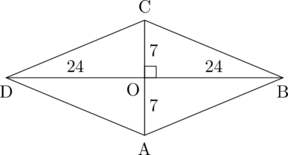
Keliling belah ketupat ABCD adalah…
Benar
Perhatikan segitiga siku-siku BOC
\(\text{BO}^2 + \text{CO}^2 = \text{BC}^2\)
\(24^2 + 7^2 = \text{BC}^2\)
\(576 + 49 = \text{BC}^2\)
\(\text{BC}^2 = 625\)
\(\text{BC} = \sqrt{625} = 25\)
Belah ketupat memiliki 4 buah sisi berukuran sama, AB = BC = CD = AD = 25
Keliling belah ketupat = 4 × panjang sisi
Keliling belah ketupat = 4 × 25 = 100
Salah
Perhatikan segitiga siku-siku BOC
\(\text{BO}^2 + \text{CO}^2 = \text{BC}^2\)
\(24^2 + 7^2 = \text{BC}^2\)
\(576 + 49 = \text{BC}^2\)
\(\text{BC}^2 = 625\)
\(\text{BC} = \sqrt{625} = 25\)
Belah ketupat memiliki 4 buah sisi berukuran sama, AB = BC = CD = AD = 25
Keliling belah ketupat = 4 × panjang sisi
Keliling belah ketupat = 4 × 25 = 100
-
Pertanyaan 10 dari 15
10. Pertanyaan
1 pointsPanjang diagonal ruang sebuah kubus dengan panjang sisi 8 cm adalah…
Benar
Kubus dengan panjang sisi \(s\) memiliki:
- panjang diagonal sisi \(s\sqrt{2}\)
- panjang diagonal ruang \(s\sqrt{3}\)
Kalian dapat menggunakan rumus pythagoras untuk membuktikan pernyataan di atas.
Jadi, panjang diagonal ruang sebuah kubus dengan panjang sisi 8 cm adalah \(8 \sqrt{3} \text{ cm}\)
Salah
Kubus dengan panjang sisi \(s\) memiliki:
- panjang diagonal sisi \(s\sqrt{2}\)
- panjang diagonal ruang \(s\sqrt{3}\)
Kalian dapat menggunakan rumus pythagoras untuk membuktikan pernyataan di atas.
Jadi, panjang diagonal ruang sebuah kubus dengan panjang sisi 8 cm adalah \(8 \sqrt{3} \text{ cm}\)
-
Pertanyaan 11 dari 15
11. Pertanyaan
1 pointsBerikut ini adalah trapezium sama kaki ABCD dengan CD = 5 cm, AB = 15 cm, dan tinggi trapezium 4 cm.
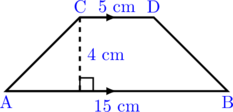
Keliling trapezium sama kaki ABCD adalah…
Benar
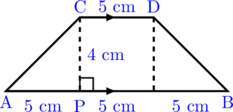
Perhatikan segitiga siku-siku APC
\(\text{AP}^2 + \text{PC}^2 = \text{AC}^2\)
\(5^2 + 4^2 = \text{AC}^2\)
\(25 + 16 = \text{AC}^2\)
\(\text{AC}^2 = 41 \)
\(\text{AC} = \sqrt{41} \text{ cm}\)
Karena trapezium sama kaki, maka \(\text{AC} = \text{BD} = \sqrt{41} \text{ cm}\)
Keliling trapezium = AB + BD + CD + AC
Keliling trapezium = 15 + \(\sqrt{41} \) + 5 + \(\sqrt{41} \)
Keliling trapezium = 20 + \(2\sqrt{41} \text{ cm} \)
Salah
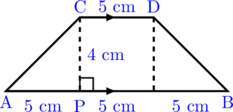
Perhatikan segitiga siku-siku APC
\(\text{AP}^2 + \text{PC}^2 = \text{AC}^2\)
\(5^2 + 4^2 = \text{AC}^2\)
\(25 + 16 = \text{AC}^2\)
\(\text{AC}^2 = 41 \)
\(\text{AC} = \sqrt{41} \text{ cm}\)
Karena trapezium sama kaki, maka \(\text{AC} = \text{BD} = \sqrt{41} \text{ cm}\)
Keliling trapezium = AB + BD + CD + AC
Keliling trapezium = 15 + \(\sqrt{41} \) + 5 + \(\sqrt{41} \)
Keliling trapezium = 20 + \(2\sqrt{41} \text{ cm} \)
-
Pertanyaan 12 dari 15
12. Pertanyaan
1 pointsLuas segi enam beraturan dengan sisi 16 cm adalah…
Benar
Segi enam beraturan terbentuk dari enam buah segitiga sama sisi seperti pada gambar di bawah ini.
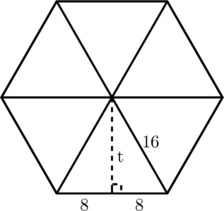
Perhatikan salah satu segitiga sama sisi.
Tinggi segitiga dapat dicari menggunakan rumus Pythagoras.
\(8^2 + t^2 = 16^2\)
\(64 + t^2 = 256\)
\(t^2 = 256 \:-\:64\)
\(t^2 = 192\)
\(t = \sqrt{192} \text{ cm}\)
\(t = \sqrt{64 \times 3} \text{ cm}\)
\(t = 8\sqrt{3} \text{ cm}\)
Luas segitiga sama sisi = \(\dfrac{1}{2} \times 16 \times 8\sqrt{3}\)
Luas segitiga sama sisi = \(\dfrac{1}{\cancel{2}} \times \cancelto{8}{16} \times 8\sqrt{3}\)
Luas segitiga sama sisi = \(64\sqrt{3} \text{ cm}^2\)
Luas segi enam beraturan = \(6 \times \text{ luas segitiga sama sisi}\)
Luas segi enam beraturan = \(6 \times 64\sqrt{3} \text{ cm}^2\)
Luas segi enam beraturan = \(384\sqrt{3} \text{ cm}^2\)
Salah
Segi enam beraturan terbentuk dari enam buah segitiga sama sisi seperti pada gambar di bawah ini.

Perhatikan salah satu segitiga sama sisi.
Tinggi segitiga dapat dicari menggunakan rumus Pythagoras.
\(8^2 + t^2 = 16^2\)
\(64 + t^2 = 256\)
\(t^2 = 256 \:-\:64\)
\(t^2 = 192\)
\(t = \sqrt{192} \text{ cm}\)
\(t = \sqrt{64 \times 3} \text{ cm}\)
\(t = 8\sqrt{3} \text{ cm}\)
Luas segitiga sama sisi = \(\dfrac{1}{2} \times 16 \times 8\sqrt{3}\)
Luas segitiga sama sisi = \(\dfrac{1}{\cancel{2}} \times \cancelto{8}{16} \times 8\sqrt{3}\)
Luas segitiga sama sisi = \(64\sqrt{3} \text{ cm}^2\)
Luas segi enam beraturan = \(6 \times \text{ luas segitiga sama sisi}\)
Luas segi enam beraturan = \(6 \times 64\sqrt{3} \text{ cm}^2\)
Luas segi enam beraturan = \(384\sqrt{3} \text{ cm}^2\)
-
Pertanyaan 13 dari 15
13. Pertanyaan
1 pointsSebuah kerucut memiliki panjang jari-jari alas 14 cm dan tinggi kerucut 48 cm. Panjang garis pelukis kerucut tersebut adalah… cm
Benar
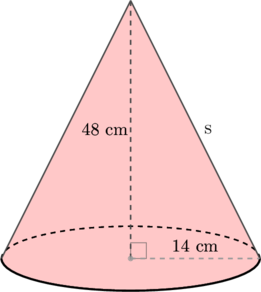
Panjang garis pelukis = \(s\)
Gunakan rumus Pythagoras
\(r^2 + t^2 = s^2\)
\(14^2 + 48^2 = s^2\)
\(196 + 2304 = s^2\)
\(s^2 = 2500\)
\(s = \sqrt{2500} = 50 \text{ cm}\)
Jadi, panjang garis pelukis kerucut tersebut adalah 50 cm.
Salah

Panjang garis pelukis = \(s\)
Gunakan rumus Pythagoras
\(r^2 + t^2 = s^2\)
\(14^2 + 48^2 = s^2\)
\(196 + 2304 = s^2\)
\(s^2 = 2500\)
\(s = \sqrt{2500} = 50 \text{ cm}\)
Jadi, panjang garis pelukis kerucut tersebut adalah 50 cm.
-
Pertanyaan 14 dari 15
14. Pertanyaan
1 pointsSebuah tangga yang panjangnya 8 meter disandarkan pada sebuah dinding yang tingginya 4 m. Jika kaki tangga itu terletak 3 m dari dinding, panjang bagian tangga yang menonjol di atas dinding adalah… meter.
Benar
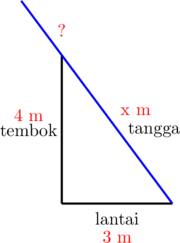
Menentukan panjang \(x\)
\(3^2 + 4^2 = x^2\)
\(9 + 16 = x^2\)
\(x^2 = 25\)
\(x = \sqrt{25} = 5 \text{ m}\)
Panjang bagian tangga yang menonjol di atas dinding adalah 8 m − 5 m = 3 meter.
Salah

Menentukan panjang \(x\)
\(3^2 + 4^2 = x^2\)
\(9 + 16 = x^2\)
\(x^2 = 25\)
\(x = \sqrt{25} = 5 \text{ m}\)
Panjang bagian tangga yang menonjol di atas dinding adalah 8 m − 5 m = 3 meter.
-
Pertanyaan 15 dari 15
15. Pertanyaan
1 pointsBerikut ini adalah ukuran sisi-sisi pada suatu segitiga siku-siku.
1) 3 m, 5 m, dan 4 m
2) 8 m, 10 m, dan 6 m
3) 13 m, 12 m, dan 5 m
4) 15 m, 8 cm, dan 17 m
Segitiga siku-siku dengan luas terbesar adalah nomor…
Benar
Luas segitiga = ½ × alas × tinggi
Sisi yang menjadi alas dan tinggi pada segitiga siku-siku bukanlah sisi miring (sisi terpanjang). Jadi untuk menghitung luas segitiga tidak menggunakan sisi terpanjang.
Luas segitiga pertama = ½ × 3 × 4 = 6 m²
Luas segitiga kedua = ½ × 6 × 8 = 24 m²
Luas segitiga ketiga= ½ × 5 × 12 = 30 m²
Luas segitiga keempat = ½ × 8 × 15 = 60 m² (luas terbesar)
Salah
Luas segitiga = ½ × alas × tinggi
Sisi yang menjadi alas dan tinggi pada segitiga siku-siku bukanlah sisi miring (sisi terpanjang). Jadi untuk menghitung luas segitiga tidak menggunakan sisi terpanjang.
Luas segitiga pertama = ½ × 3 × 4 = 6 m²
Luas segitiga kedua = ½ × 6 × 8 = 24 m²
Luas segitiga ketiga= ½ × 5 × 12 = 30 m²
Luas segitiga keempat = ½ × 8 × 15 = 60 m² (luas terbesar)
