Soal 01
Koordinat titik puncak grafik fungsi kuadrat \(f(x) = -x^2 + 4x\: -\: 12\) beserta jenisnya adalah…
(A) Titik balik minimum \((2, -8)\)
(B) Titik balik maksimum \((2, -8)\)
(C) Titik balik minimum \((8, -4)\)
(D) Titik balik maksimum \((8, -4)\)
Jawaban: B
\(f(x) = -x^2 + 4x \:-\: 12\)
\(a = -1\) Karena nilai \(a\) negatif, maka jenis titik baliknya adalah maksimum.
\(b = 4\)
\(x_p = – \dfrac{b}{2a}\)
\(x_p = – \dfrac{4}{2(-1)}\)
\(x_p = 2\)
Substitusikan nilai \(x = 2\) ke dalam persamaan \(f(x) = -x^2 + 4x\: -\: 12\)
\(f(2) = -(2)^2 + 4(2) \:-\: 12\)
\(f(2) = -4 + 8 \:-\: 12\)
\(f(2) = -8\)
Jadi, koordinat titik puncak grafik fungsi kuadrat \(f(x) = -x^2 + 4x\: -\: 12\) berada di titik \((2, -8)\) dan merupakan titik balik maksimum.
Soal 02
Grafik fungsi kuadrat \(f(x) = 3x^2 + 6x + 2a\:-\:1\) memotong sumbu Y di titik \((0, -3)\). Nilai \(a\) yang memenuhi adalah…
(A) \(-2\)
(B) \(-1\)
(C) \(0\)
(D) \(1\)
Jawaban: B
Grafik fungsi kuadrat \(f(x) = 3x^2 + 6x + 2a\:-\:1\) memotong sumbu Y di titik \((0, -3)\).
Substitusikan titik \((0, -3)\) ke \(f(x) = 3x^2 + 6x + 2a\:-\:1\).
\(-3 = 3(0)^2 + 6(0) + 2a\:-\:1\)
\(-3 = 2a\:-\:1\)
\(-3 + 1 = 2a\)
\(-2 = 2a\)
\(a = -1\)
Jadi, nilai \(a\) yang memenuhi adalah \(-1\).
Soal 03
Grafik fungsi kuadrat memiliki nilai minimum 3 untuk \(x = -2\) dan memiliki nilai \(39\) untuk \(x = 4\). Persamaan fungsi kuadrat tersebut adalah…
(A) \(f(x) = 2x^2 + 3x + 1\)
(B) \(f(x) = x^2 + 3x + 5\)
(C) \(f(x) = x^2 + 4x \:-\: 7\)
(D) \(f(x) = x^2 + 4x + 7\)
Jawaban: D
Grafik fungsi kuadrat memiliki nilai minimum 3 untuk \(x = -2\) maka koordinat titik balik minimum berada di titik \((-2, 3)\).
\((x_p, y_p) = (-2, 3)\)
Menentukan persamaan fungsi kuadrat
\(f(x) = a(x\:-\:x_p)^2 + y_p\)
\(f(x) = a(x + 2)^2 + 3\)
Grafik memiliki nilai \(39\) untuk \(x = 4\) artinya grafik fungsi kuadrat juga melalui titik \((4, 39)\).
\(f(4) = a(x + 2)^2 + 3\)
\(39 = a(4 + 2)^2 + 3\)
\(39\:-\: 3 = 36a\)
\(36 = 36a\)
\(a = 1\)
Substitusikan \(a = 1\) ke persamaan \(f(x) = a(x + 2)^2 + 3\)
\(f(x) = (x + 2)^2 + 3\)
\(f(x) = x^2 + 4x + 4 + 3\)
\(f(x) = x^2 + 4x + 7\)
Jadi, persamaan grafik fungsi kuadratnya adalah \(f(x) = x^2 + 4x + 7\).
Soal 04
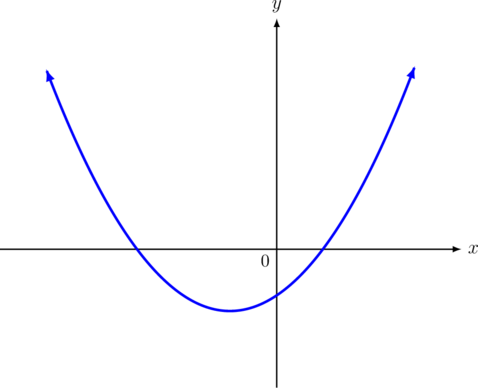
Diberikan persamaan fungsi kuadrat berikut:
(1) \(f(x) = \dfrac{1}{3}x^2 + \dfrac{2}{3}x \:-\:1\)
(2) \(f(x) = 2x^2 \:-\:8x + 6\)
(3) \(f(x) = \dfrac{1}{4}x^2 + \dfrac{1}{2}x \:-\:2\)
(4) \(f(x) = -\dfrac{1}{3}x^2 + \dfrac{2}{3}x \:-\:1\)
Persamaan yang mungkin dari sketsa grafik fungsi kuadrat tersebut adalah…
(A) (1) dan (2)
(B) (1) dan (3)
(C) (2) dan (3)
(D) (2) dan (4)
Jawaban: B
Grafik fungsi kuadrat berbentuk parabola yang membuka ke atas, sehingga nilai \(a\) positif.
Fungsi kuadrat nomor (4) salah karena nilai \(a\) negatif
Grafik fungsi kuadrat memotong sumbu x negatif dan sumbu x positif.
Fungsi kuadrat nomor (2) salah karena \(f(x) = 2x^2 \:-\:8x + 6\) memiliki dua titik potong terhadap sumbu x positif.
\(0 = 2x^2 \:-\:8x + 6\)
\(0 = (2x\:-\:6)(x\:-\:1)\)
\(2x\:-\:6 = 0 \rightarrow x = 3\)
\(x\:-\:1 = 0 \rightarrow x = 1\)
Titik potong \(f(x) = 2x^2 \:-\:8x + 6\) terhadap sumbu X berada di titik (3, 0) dan (1, 0)
Soal 05
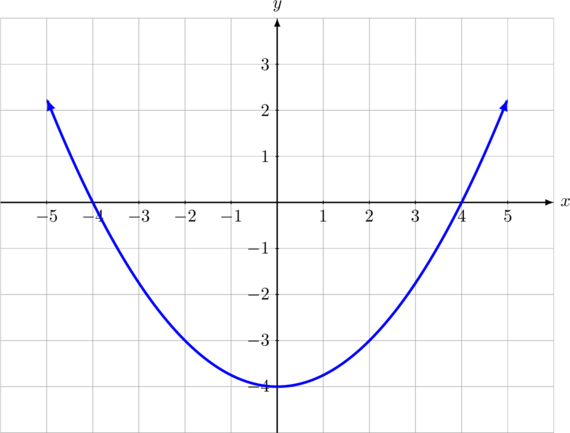
Persamaan fungsi kuadrat di atas adalah…
(A) \(f(x) = \dfrac{1}{2}x^2 + 3\)
(B) \(f(x) = \dfrac{1}{2}x^2 \:-\:4\)
(C) \(f(x) = \dfrac{1}{4}x^2 + 4\)
(D) \(f(x) = \dfrac{1}{4}x^2 \:-\:4\)
Jawaban: D
Grafik fungsi kuadrat memotong sumbu X di titik (-4, 0) dan (4, 0).
\(\color{blue} f(x) = a(x\:-\:x_1)(x\:-\:x_2)\)
\(f(x) = a(x + 4)(x\:-\:4)\)
Grafik juga melalui titik potong sumbu Y di (0, -4)
\(-4 = a(0 + 4)(0\:-\:4)\)
\(-4 = -16a\)
\(a = \dfrac{1}{4}\)
\(f(x) = \dfrac{1}{4}(x + 4)(x\:-\:4)\)
\(f(x) = \dfrac{1}{4}(x^2 \:-\:16)\)
\(f(x) = \dfrac{1}{4}x^2 \:-\:4\)
Soal 06
Terdapat persamaan fungsi kuadrat:
(1) \(f(x) = 2x^2 + x \:-\: 3\)
(2) \(f(x) = x^2 + 2x + 5\)
(3) \(f(x) = 2x^2 + x + 3\)
(4) \(f(x) = -x^2 + x + 5\)
Fungsi kuadrat yang grafiknya tidak memotong maupun menyinggung sumbu X adalah…
(A) (1) dan (2)
(B) (2) dan (3)
(C) (1) dan (4)
(D) (2) dan (4)
Jawaban: B
Fungsi kuadrat dengan nilai diskriminan negatif grafiknya tidak akan memotong maupun menyinggung sumbu X.
\(\textbf{D} = b^2 \:-\: 4ac\)
\(f(x) = 2x^2 + x \:-\: 3\)
\(a = 2, b = 1, c = -3\)
\(\textbf{D} = b^2 \:-\: 4ac\)
\(\textbf{D} = 1^2 \:-\: 4(2)(-3) = 25 > 0\)
\(\color{blue}f(x) = x^2 + 2x + 5\)
\(a = 1, b = 2, c = 5\)
\(\textbf{D} = b^2 \:-\: 4ac\)
\(\textbf{D} = 2^2 \:-\: 4(1)(5) = -16 < 0\)
\(\color{blue} f(x) = 2x^2 + x + 3\)
\(a = 2, b = 1, c = 3\)
\(\textbf{D} = b^2 \:-\: 4ac\)
\(\textbf{D} = 1^2 \:-\: 4(2)(3) = -23 < 0\)
\(f(x) = -x^2 + x + 5\)
\(a = -1, b = 1, c = 5\)
\(\textbf{D} = b^2 \:-\: 4ac\)
\(\textbf{D} = 1^2 \:-\: 4(-1)(5) = 21 > 0\)
Jadi, fungsi kuadrat yang grafiknya tidak memotong maupun menyinggung sumbu X adalah (2) dan (3).
Soal 07
Terdapat persamaan fungsi kuadrat:
(1) \(f(x) = x^2 + 3x \:-\: 1\)
(2) \(f(x) = x^2 + 5x + 3\)
(3) \(f(x) = 2x^2 +2x + 5\)
(4) \(f(x) = -x^2 + x \:-\: 5\)
Fungsi kuadrat yang grafiknya memotong sumbu Y negatif adalah…
(A) (1) dan (2)
(B) (2) dan (3)
(C) (1) dan (4)
(D) (2) dan (4)
Jawaban: C
Fungsi kuadrat dengan nilai \(c\) negatif grafiknya memotong sumbu Y negatif.
(1) \(f(x) = x^2 + 3x \color{blue}\:-\: 1\)
(2) \(f(x) = x^2 + 5x + 3\)
(3) \(f(x) = 2x^2 +2x + 5\)
(4) \(f(x) = -x^2 + x \color{blue}\:-\: 5\)
Dari persamaan fungsi kuadrat di atas, fungsi kuadrat (1) dan (4) memiliki nilai \(c\) yang negatif.
Soal 08
Diberikan fungsi kuadrat \(f(x) = ax^2 \:-\:4x + 3\). Tentukan batas nilai \(a\) agar fungsi \(f(x)\) selalu bernilai positif.
Jawaban:
Fungsi \(f(x)\) selalu bernilai positif, artinya definit positif.
Grafiknya selalu berada di atas sumbu X.
Syarat definit positif:
(1) \(\textbf{D} < 0\)
(2) \(a > 0\)
\(f(x) = ax^2 \:-\:4x + 3\)
\(\textbf{D} = b^2\:-\:4ac < 0\)
\((-4)^2\:-\:4a(3) < 0\)
\(16\:-\:12a < 0\)
\(-12a < -16\)
Bagi kedua ruas dengan \(-12\)
\(a > \dfrac{16}{12}\)
\(a > \dfrac{4}{3}\dotso \color{red} (1)\)
\(a > 0\dotso \color{red} (2)\)
Irisan penyelesaian (1) dan (2) adalah \(a > \dfrac{4}{3}\).
Jadi, batas nilai \(a\) agar fungsi kuadrat selalu bernilai positif adalah \(a > \dfrac{4}{3}\).
Soal 09
Terdapat persamaan fungsi kuadrat:
(1) \(f(x) = -3x^2 \:-\:5x \:-\: 4\)
(2) \(f(x) = -5x^2\:-\: 2x + 3\)
(3) \(f(x) = -2x^2 + x \:-\:6\)
(4) \(f(x) = -3x^2 \:-\:2x + 3\)
Fungsi kuadrat yang selalu bernilai negatif adalah…
(A) (1) dan (2)
(B) (1) dan (3)
(C) (1) dan (4)
(D) (2) dan (4)
Jawaban: B
Fungsi \(f(x)\) selalu bernilai negatif, artinya definit negatif.
Grafiknya selalu berada di bawah sumbu X.
Syarat definit negatif:
(1) \(\textbf{D}= b^2\:-\:4ac < 0\)
(2) \(a < 0\)
\(f(x) = -3x^2 \:-\:5x \:-\: 4\) → definit negatif
\(\textbf{D} = (-5)^2 \:-\:4(-3)(-4) = -23 <0\)
\(a = -3 < 0\)
\(f(x) = -5x^2\:-\: 2x + 3\)
\(\textbf{D} = (-2)^2 \:-\:4(-5)(3) = 64 > 0\)
\(a = -5 < 0\)
\(f(x) = -2x^2 + x \:-\:6\)
\(\textbf{D} = 1^2 \:-\:4(-2)(-6) = -47 < 0\) → definit negatif
\(a = -2 < 0\)
\(f(x) = -3x^2 \:-\:2x + 3\)
\(\textbf{D} = (-2)^2 \:-\:4(-3)(3) = 40 > 0\)
\(a = -3 < 0\)
Soal 10
Seorang pemain golf memukul bola dengan kecepatan awal \(\textbf{V}_0\) m/s sehingga melambung ke udara. Tinggi bola setelah \(t\) detik adalah \(h(t)\) meter. Bola yang melambung di udara dipengaruhi oleh gaya gravitasi bumi (\(g = 10 \text{ m/s²}\)). Ketinggian bola memenuhi persamaan fungsi kuadrat \(h(t) = \textbf{V}_0\cdot t \:-\: \dfrac{1}{2} g t^2\). Jika kecepatan awal \(\textbf{V}_0 = 15 \text{ m/s}\), tinggi maksimum bola golf tersebut adalah…
(A) 11,25 meter
(B) 11,50 meter
(C) 22,25 meter
(D) 22,50 meter
(E) 23,50 meter
Jawaban: A
\(h(t) = \textbf{V}_0\cdot t \:-\: \dfrac{1}{2} g t^2\)
\(h(t) = 15t \:-\: \dfrac{1}{2} \cdot 10 \cdot t^2\)
\(h(t) = 15t \:-\: 5t^2\)
\(a = -5\)
\(b = 15\)
Bola mencapai ketinggian maksimum saat \(t = – \dfrac{b}{2a}\)
\(t_{\text{max}} = -\dfrac{15}{2(-5)}\)
\(t_{\text{max}} = \dfrac{15}{10}\)
\(t_{\text{max}} = \dfrac{3}{2} \text{ detik}\)
Substitusikan \(t_{\text{max}} = \dfrac{3}{2} \text{ detik}\) ke dalam persamaan \(h(t) = 15t \:-\: 5t^2\)
\(h \left(\dfrac{3}{2} \right) = 15 \cdot \dfrac{3}{2} \:-\: 5 \cdot \left( \dfrac{3}{2} \right)^2\)
\(h \left(\dfrac{3}{2} \right) = \dfrac{45}{2} \:-\: 5 \cdot \dfrac{9}{4}\)
\(h \left(\dfrac{3}{2} \right) = \dfrac{90}{4} \:-\: \dfrac{45}{4}\)
\(h \left(\dfrac{3}{2} \right) = \dfrac{45}{4} \text{ meter}\)
\(h \left(\dfrac{3}{2} \right) = 11,25 \text{ meter}\)
Jadi, ketinggian maksimum yang dicapai bola golf tersebut adalah 11,25 meter.
