Soal 01
Diketahui limas tegak T.ABCD dengan alas berbentuk persegi, AB = 6 satuan dan AT = 10 satuan. Jika P adalah titik potong antara garis DM dan AC, tentukan jarak antara titik T dan P.

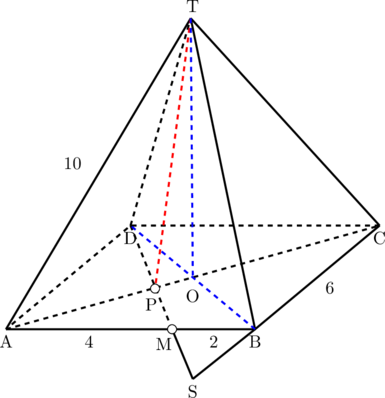
Langkah 1: menentukan panjang SB
\(\triangle \text{SBM} \sim \triangle \text{SCD}\)
\(\dfrac{\text{SB}}{\text{SC}} = \dfrac{\text{MB}}{\text{CD}}\)
\(\dfrac{\text{SB}}{\text{SB} + 6} = \dfrac{2}{6}\)
\(\dfrac{\text{SB}}{\text{SB} + 6} = \dfrac{1}{3}\)
\(3 \text{SB} = \text{SB} + 6\)
\(2 \text{SB} = 6\)
\(\text{SB} = 3 \text{ satuan}\)
Langkah 2: menentukan panjang AP
\(\triangle \text{APD} = \triangle \text{CPS}\)
\(\dfrac{\text{AD}}{\text{SC}} = \dfrac{\text{AP}}{\text{PC}}\)
\(\dfrac{6}{9} = \dfrac{\text{AP}}{6\sqrt{2}\:-\:\text{AP}}\)
\(\dfrac{2}{3} = \dfrac{\text{AP}}{6\sqrt{2}\:-\:\text{AP}}\)
\(12\sqrt{2}\:-\:2\text{AP}= 3\text{AP}\)
\(12\sqrt{2}= 5\text{AP}\)
\(\text{AP} = \dfrac{12}{5} \sqrt{2} \text{ satuan}\)
Langkah 3: menentukan panjang TO
Perhatikan segitiga siku-siku TOA
\(\text{AO}^2 + \text{TO}^2 = \text{AT}^2\)
\((3\sqrt{2})^2 + \text{TO}^2 = 10^2\)
\(18 + \text{TO}^2 = 100\)
\(\text{TO}^2 = 100 \:-\: 18\)
\(\text{TO}^2 = 82\)
\(\text{TO} = \sqrt{82} \text{ satuan}\)
Langkah 4: menentukan panjang PO
\(\text{PO} = \text{AO}\:-\:\text{AP}\)
\(\text{PO} = 3\sqrt{2}\:-\: \dfrac{12}{5} \sqrt{2}\)
\(\text{PO} =\dfrac{3}{5} \sqrt{2}\text{ satuan}\)
Langkah 5: menentukan panjang TP
Lihat segitiga siku-siku TOP
\(\text{PO}^2 + \text{TO}^2 = \text{TP}^2\)
\(\left( \dfrac{3}{5} \sqrt{2} \right)^2 + (\sqrt{82})^2 = \text{TP}^2\)
\(\dfrac{18}{25} + 82 = \text{TP}^2\)
\(\dfrac{2068}{25} = \text{TP}^2\)
\(\text{TP} = \sqrt{\dfrac{2068}{25}}\)
\(\text{TP} =\dfrac{2\sqrt{517}}{5} \text{ satuan}\)
Jadi, jarak antara titik T ke P adalah \(\color{blue} \dfrac{2\sqrt{517}}{5} \text{ satuan}\)
Soal 02
Diketahui kubus ABCD.EFGH dengan panjang rusuk 5 satuan dan titik P berapa pada AB dengan AP = 2PB. Jika titik K adalah perpotongan antara ruas garis AG dan HP, jarak titik F ke titik K adalah… satuan.
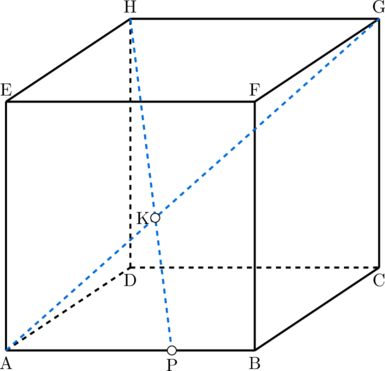
Langkah 1: menentukan perbandingan PK dan KH
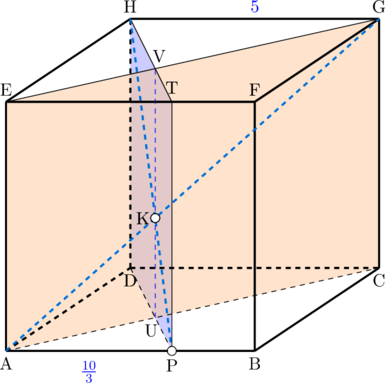
\(\triangle \text{AKP} \sim \triangle \text{GKH}\)
\(\dfrac{\text{AP}}{\text{GH}} = \dfrac{\text{PK}}{\text{HK}}\)
\(\dfrac{\frac{10}{3}}{5} = \dfrac{\text{PK}}{\text{HK}}\)
\(\dfrac{2}{3} = \dfrac{\text{PK}}{\text{HK}}\)
\(\text{PK} : \text{HK} = 2 : 3\)
Langkah 2: menentukan panjang UK
\(\triangle \text{PUK} \sim \triangle \text{HVK}\)
\(\dfrac{\text{PK}}{\text{HK}} = \dfrac{\text{UK}}{\text{VK}}\)
\(\dfrac{2}{3} = \dfrac{\text{UK}}{\text{VK}}\)
\(\text{UK} : \text{VK} = 2 : 3\)
\(\text{UK} = \dfrac{2}{2 + 3} \times 5\)
\(\text{UK} = 2 \text{ satuan}\)
Langkah 3: menentukan panjang FK menggunakan cara vektor 3D
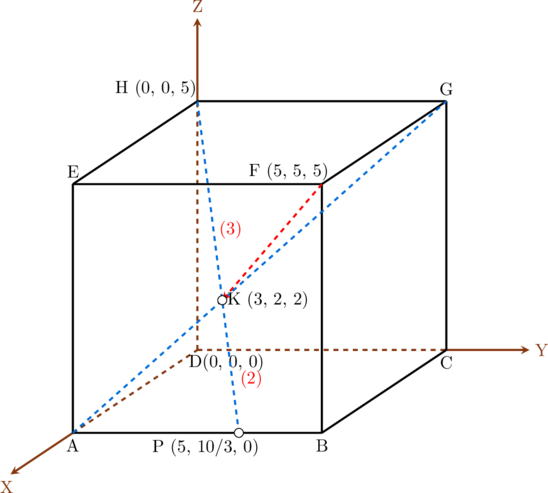
Koordinat K dapat dicari dari perbandingan ruas garis HP
\(\textbf{K} = \dfrac{2\left(\begin{array}{c}0\\0\\5\end{array}\right)+ 3\left(\begin{array}{c}5\\ \frac{10}{3}\\0\end{array}\right)}{2 + 3}\)
\(\textbf{K} = \dfrac{\left(\begin{array}{c}15\\10\\10\end{array}\right)}{5}\)
\(\textbf{K} = \left(\begin{array}{c}3\\2\\2\end{array}\right)\)
Menentukan vektor FK
\(\textbf{FK} = \textbf{k}\:-\:\textbf{f}\)
\(\textbf{FK} = \left(\begin{array}{c}3\\2\\2\end{array}\right)\:-\: \left(\begin{array}{c}5\\5\\5\end{array}\right)\)
\(\textbf{FK} = \left(\begin{array}{c}-2\\-3\\-3\end{array}\right)\)
\(\textbf{|FK|} = \sqrt{(-2)^2 + (-3)^2 + (-3)^2}\)
\(\textbf{|FK|} = \sqrt{22}\)
Jadi, jarak antara titik F dengan titik K adalah \(\color{blue} \sqrt{22} \text{ satuan}\)
