Contoh Soal 01
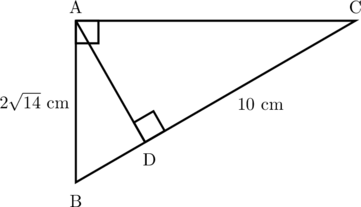
Tentukan panjang:
(A) BD
(B) AC
(C) AD
Menentukan panjang BD
\(\color{blue} \textbf{AB}^2 = \textbf{BD} \times \textbf{BC}\)
\((2\sqrt{14})^2 = \textbf{BD} \times (\textbf{BD} + 10)\)
\(56 = \textbf{BD}^2 + 10 \textbf{BD}\)
\(\textbf{BD}^2 + 10 \textbf{BD}\:-\:56 = 0\)
\((\textbf{BD} + 14)(\textbf{BD}\:-\:4 ) = 0\)
\(\textbf{BD} + 14 = 0 \rightarrow \textbf{BD} = -14 \dotso \color{red} \text{ TM}\)
\(\textbf{BD} \:-\: 4 = 0 \rightarrow \textbf{BD} = 4 \)
Jadi, panjang BD adalah 4 cm.
Menentukan panjang AC
\(\color{blue} \textbf{AC}^2 = \textbf{CD} \times \textbf{CB}\)
\(\textbf{AC}^2 = 10 \times (10 + 4)\)
\(\textbf{AC}^2 = 140\)
\(\textbf{AC} = \sqrt{140} = 2\sqrt{35}\)
Jadi, panjang AC adalah \(2\sqrt{35}\) cm.
Menentukan panjang AD
\(\color{blue} \textbf{AD}^2 = \textbf{DB} \times \textbf{DC}\)
\(\textbf{AD}^2 = 4 \times 10\)
\(\textbf{AD} = \sqrt{40} = 2\sqrt{10}\text{ cm}\)
Jadi, panjang AD adalah \(2\sqrt{10}\) cm.
Contoh Soal 02
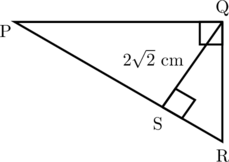
Diketahui panjang QS = \(2\sqrt{2}\) cm dan panjang PR = 6 cm.
Tentukan panjang:
(A) SR
(B) SP
(C) QR
(D) QP
Menentukan panjang SR dan SP
Misal panjang SR adalah x cm, maka panjang SP = (6 − x) cm
\(\color{blue} \textbf{QS}^2 = \textbf{SR} \times \textbf{SP}\)
\((2\sqrt{2})^2 =x \times (6\:-\:x)\)
\(8 = 6x\:-\:x^2\)
\(x^2\:-\:6x + 8 = 0\)
\((x\:-\:4)(x\:-\:2) = 0\)
\(x\:-\:4 = 0 \rightarrow x = 4 \text{ cm}\)
\(x\:-\:2 = 0 \rightarrow x = 2 \text{ cm}\)
Karena SR lebih pendek dari SP maka SR = 2 cm dan SP = (6 − 2) = 4 cm
Menentukan panjang QR
\(\color{blue} \textbf{QR}^2 = \textbf{RS} \times \textbf{RP}\)
\(\textbf{QR}^2 = 2 \times 6\)
\(\textbf{QR}^2 = 12\)
\(\textbf{QR} = \sqrt{12} = 2\sqrt{3}\text{ cm}\)
Jadi, panjang QR adalah \( 2\sqrt{3}\text{ cm}\)
Menentukan panjang QP
\(\color{blue} \textbf{QP}^2 = \textbf{PS} \times \textbf{PR}\)
\(\textbf{QP}^2 = 4 \times 6\)
\(\textbf{QP}^2 = 24\)
\(\textbf{QP} = \sqrt{24} = 2\sqrt{6}\text{ cm}\)
Jadi, panjang QP adalah \( 2\sqrt{6}\text{ cm}\)
