Quiz-summary
0 of 20 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Halo, teman-teman!
Selamat datang di Tryout Penalaran Matematika UTBK.
Kalian akan mengerjakan 20 soal PM dalam waktu maksimal 42,5 menit. Bacalah setiap soal dengan cermat, pahami pertanyaannya, dan pilih jawaban yang paling tepat. Tetap fokus dan percaya diri dalam mengerjakan soal.
Jadikan tryout ini sebagai sarana untuk mengasah kemampuan dan meningkatkan kesiapan kalian menghadapi UTBK.
Selamat mengerjakan, semoga sukses!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 20 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 20
1. Pertanyaan
1 pointsUTBK 2023
Seorang pedagang kacang rebus menggunakan alat takar besar, sedang, dan kecil untuk menakar banyaknya kacang yang dijual. Kacang sebanyak 1 takaran besar dan 2 takaran sedang dijual seharga Rp26.000,00, sementara kacang sebanyak 1 takaran besar dan 2 takaran kecil dijual seharga Rp20.000,00.
Jika Siti membeli kacang sebanyak 4 takaran besar, 4 takaran sedang, dan 4 takaran kecil, ia harus membayar sebanyak…
Benar
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Jumlahkan persamaan (1) dan (2)
2B + 2S + 2K = 46.000
Kali kedua ruas dengan 2
4B + 4S + 4K = Rp92.000,00
Jadi, Siti harus membayar sebanyak Rp92.000,00
Salah
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Jumlahkan persamaan (1) dan (2)
2B + 2S + 2K = 46.000
Kali kedua ruas dengan 2
4B + 4S + 4K = Rp92.000,00
Jadi, Siti harus membayar sebanyak Rp92.000,00
-
Pertanyaan 2 dari 20
2. Pertanyaan
1 pointsUTBK 2023
Seorang pedagang kacang rebus menggunakan alat takar besar, sedang, dan kecil untuk menakar banyaknya kacang yang dijual. Kacang sebanyak 1 takaran besar dan 2 takaran sedang dijual seharga Rp26.000,00, sementara kacang sebanyak 1 takaran besar dan 2 takaran kecil dijual seharga Rp20.000,00.
Selisih harga kacang untuk 1 takaran sedang dan 1 takaran kecil adalah…
Benar
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Kurangkan persamaan (1) dengan persamaan (2)
2S − 2K = 6.000
Bagi kedua ruas dengan 2
S − K = 3.000
Jadi, selisih harga kacang untuk 1 takaran sedang dan 1 takaran kecil adalah Rp3.000,00
Salah
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Kurangkan persamaan (1) dengan persamaan (2)
2S − 2K = 6.000
Bagi kedua ruas dengan 2
S − K = 3.000
Jadi, selisih harga kacang untuk 1 takaran sedang dan 1 takaran kecil adalah Rp3.000,00
-
Pertanyaan 3 dari 20
3. Pertanyaan
1 pointsUTBK 2023
Seorang pedagang kacang rebus menggunakan alat takar besar, sedang, dan kecil untuk menakar banyaknya kacang yang dijual. Kacang sebanyak 1 takaran besar dan 2 takaran sedang dijual seharga Rp26.000,00, sementara kacang sebanyak 1 takaran besar dan 2 takaran kecil dijual seharga Rp20.000,00.
Jika Ani membawa uang sebesar Rp66.000,00, maka ia mendapat kacang sebanyak 3 takaran besar, 2 takaran sedang, dan … takaran kecil.
Benar
2B + 2S + 2K = 46.000
Bagi kedua ruas dengan 2
B + S + K = 23.000 … (3)
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Ambil, B = 10.000, maka S = 8.000 dan K = 5.000
3B + 2S + xK = 66.000
3(10.000) + 2(8.000) + x(5.000) = 66.000
46.000 + 5.000 x = 66.000
5000 x = 20.000
x = 4
Jadi, ada 4 takaran kecil.
Salah
2B + 2S + 2K = 46.000
Bagi kedua ruas dengan 2
B + S + K = 23.000 … (3)
B + 2S = 26.000 … (1)
B + 2K = 20.000 … (2)
Ambil, B = 10.000, maka S = 8.000 dan K = 5.000
3B + 2S + xK = 66.000
3(10.000) + 2(8.000) + x(5.000) = 66.000
46.000 + 5.000 x = 66.000
5000 x = 20.000
x = 4
Jadi, ada 4 takaran kecil.
-
Pertanyaan 4 dari 20
4. Pertanyaan
1 pointsUTBK 2023
Tabel di bawah ini menyatakan banyaknya siswa berkacamata pada lima SMP di Kota Bandar Lampung. Diketahui persentase siswa perempuan di SMP 1 dan SMP 2 adalah 70% masing-masing, sedangkan persentase siswa perempuan di SMP 3, SMP 4, dan SMP 5 adalah 40% masing-masing.
Sekolah Jumlah Siswa Rasio Jumlah Siswa Berkacamata dengan Jumlah Siswa Jumlah Siswa Laki-laki Berkacamata Jumlah Siswa Perempuan Berkacamata SMP 1 90 2 : 3 24 SMP 2 120 1 : 2 18 SMP 3 100 7 : 10 42 SMP 4 140 3 : 7 30 SMP 5 150 8 : 15 56 Selisih jumlah siswa laki-laki berkacamata dan perempuan yang berkacamata adalah… orang
Benar
Sekolah Jumlah Siswa Rasio Jumlah Siswa Berkacamata dengan Jumlah Siswa Jumlah Siswa Laki-laki Berkacamata Jumlah Siswa Perempuan Berkacamata SMP 1 90 \(\dfrac{2}{3}\times 90 = 60\) 24 36 SMP 2 120 \(\dfrac{1}{2}\times 120 = 60\) 18 42 SMP 3 100 \(\dfrac{7}{10}\times 100 = 70\) 42 28 SMP 4 140 \(\dfrac{3}{7}\times 140 = 60\) 30 30 SMP 5 150 \(\dfrac{8}{15}\times 150 = 80\) 56 24 Jumlah Siswa Laki-laki Berkacamata = 170
Jumlah Siswa Perempuan Berkacamata = 160
Selisihnya adalah 10 orang.
Salah
Sekolah Jumlah Siswa Rasio Jumlah Siswa Berkacamata dengan Jumlah Siswa Jumlah Siswa Laki-laki Berkacamata Jumlah Siswa Perempuan Berkacamata SMP 1 90 \(\dfrac{2}{3}\times 90 = 60\) 24 36 SMP 2 120 \(\dfrac{1}{2}\times 120 = 60\) 18 42 SMP 3 100 \(\dfrac{7}{10}\times 100 = 70\) 42 28 SMP 4 140 \(\dfrac{3}{7}\times 140 = 60\) 30 30 SMP 5 150 \(\dfrac{8}{15}\times 150 = 80\) 56 24 Jumlah Siswa Laki-laki Berkacamata = 170
Jumlah Siswa Perempuan Berkacamata = 160
Selisihnya adalah 10 orang.
-
Pertanyaan 5 dari 20
5. Pertanyaan
1 pointsUTBK 2023
Tabel di bawah ini menyatakan banyaknya siswa berkacamata pada lima SMP di Kota Bandar Lampung. Diketahui persentase siswa perempuan di SMP 1 dan SMP 2 adalah 70% masing-masing, sedangkan persentase siswa perempuan di SMP 3, SMP 4, dan SMP 5 adalah 40% masing-masing.
Sekolah Jumlah Siswa Rasio Jumlah Siswa Berkacamata dengan Jumlah Siswa Jumlah Siswa Laki-laki Berkacamata Jumlah Siswa Perempuan Berkacamata SMP 1 90 2 : 3 24 SMP 2 120 1 : 2 18 SMP 3 100 7 : 10 42 SMP 4 140 3 : 7 30 SMP 5 150 8 : 15 56 Manakah dari pernyataan berikut yang benar?
Pasangkan pada kolom Benar atau Salah untuk setiap pernyataan berikut ini.
Pasangkan
- Benar
- Benar
- Salah
-
Jumlah siswa perempuan berkacamata di SMP 1 dan SMP 2 adalah 78 orang.
-
Rasio siswa laki-laki berkacamata di SMP 2 dan SMP 4 adalah 3 : 5.
-
Rata-rata jumlah siswa laki-laki di SMP 3, SMP 4, dan SMP 5 adalah 77 orang.
Benar
Salah
-
Pertanyaan 6 dari 20
6. Pertanyaan
1 pointsUTBK 2023
Tabel di bawah ini menyatakan banyaknya siswa berkacamata pada lima SMP di Kota Bandar Lampung. Diketahui persentase siswa perempuan di SMP 1 dan SMP 2 adalah 70% masing-masing, sedangkan persentase siswa perempuan di SMP 3, SMP 4, dan SMP 5 adalah 40% masing-masing.
Sekolah Jumlah Siswa Rasio Jumlah Siswa Berkacamata dengan Jumlah Siswa Jumlah Siswa Laki-laki Berkacamata Jumlah Siswa Perempuan Berkacamata SMP 1 90 2 : 3 24 SMP 2 120 1 : 2 18 SMP 3 100 7 : 10 42 SMP 4 140 3 : 7 30 SMP 5 150 8 : 15 56 Sekolah yang memiliki jumlah siswa perempuan berkacamata terbanyak adalah…
Benar
Salah
-
Pertanyaan 7 dari 20
7. Pertanyaan
1 pointsUTBK 2023
Sebuah perusahaan swasta setiap bulannya mengalami kenaikan keuntungan tetap. Oleh karena itu, perusahaan tersebut akan menaikkan gaji beberapa pegawai yang memenuhi kriteria setiap bulannya. Kriterianya dapat dilihat pada tabel berikut.
Jabatan Gaji Bulan Pertama Besar Kenaikan Setiap Bulan Manajer Rp15.000.000,00 Rp200.000,00 Administrasi Rp7.000.000,00 Rp150.000,00 Staf Rp5.000.000,00 Rp100.000,00 Jika Irawan merupakan pegawai baru di perusahaan tersebut dengan jabatan sebagai Manager. Jumlah gaji Irawan dalam 1 tahun sebesar…
Benar
\(\text{S}_n = \dfrac{n}{2}(2a + (n\:-\:1)b)\)
\(\text{S}_{12} = \dfrac{12}{2}(2\cdot 15.000.000 + (12\:-\:1)\cdot 200.000)\)
\(\text{S}_{12} = 193.200.000\)
Salah
\(\text{S}_n = \dfrac{n}{2}(2a + (n\:-\:1)b)\)
\(\text{S}_{12} = \dfrac{12}{2}(2\cdot 15.000.000 + (12\:-\:1)\cdot 200.000)\)
\(\text{S}_{12} = 193.200.000\)
-
Pertanyaan 8 dari 20
8. Pertanyaan
1 pointsUTBK 2023
Sebuah perusahaan swasta setiap bulannya mengalami kenaikan keuntungan tetap. Oleh karena itu, perusahaan tersebut akan menaikkan gaji beberapa pegawai yang memenuhi kriteria setiap bulannya. Kriterianya dapat dilihat pada tabel berikut.
Jabatan Gaji Bulan Pertama Besar Kenaikan Setiap Bulan Manajer Rp15.000.000,00 Rp200.000,00 Administrasi Rp7.000.000,00 Rp150.000,00 Staf Rp5.000.000,00 Rp100.000,00 Staf baru akan mendapatkan gaji bulanan sebesar Rp7.000.000,00 pada bulan ke-…
Benar
\(\text{U}_n = a + (n\:-\:1)b\)
\(7.000.000 = 5.000.000 + (n\:-\:1)\cdot 100.000\)
\(n = 21\)
Salah
\(\text{U}_n = a + (n\:-\:1)b\)
\(7.000.000 = 5.000.000 + (n\:-\:1)\cdot 100.000\)
\(n = 21\)
-
Pertanyaan 9 dari 20
9. Pertanyaan
1 pointsUTBK 2024
Pendapatan seorang youtuber didapat dari iklan yang tayang di setiap video yang dia buat. Pendapatan dari iklan dihitung Rp3.000,00 per iklan. Dalam setiap video terdapat 2 iklan di awal video dan 1 iklan setiap 10 menit video berjalan.
Jika suatu video mempunyai \(x\) menit durasi, maka banyak iklan maksimal yang dapat tayang dapat dirumuskan oleh persamaan…
Benar
\(2 + \dfrac{x}{10}\)
\(2 + 0,1x\)
Salah
\(2 + \dfrac{x}{10}\)
\(2 + 0,1x\)
-
Pertanyaan 10 dari 20
10. Pertanyaan
1 pointsUTBK 2024
Pendapatan seorang youtuber didapat dari iklan yang tayang di setiap video yang dia buat. Pendapatan dari iklan dihitung Rp3.000,00 per iklan. Dalam setiap video terdapat 2 iklan di awal video dan 1 iklan setiap 10 menit video berjalan.
Jika terdapat \(y\) iklan dalam satu video, maka pendapatan maksimal video tersebut adalah…
Benar
Salah
-
Pertanyaan 11 dari 20
11. Pertanyaan
1 pointsUTBK 2024
Pendapatan seorang youtuber didapat dari iklan yang tayang di setiap video yang dia buat. Pendapatan dari iklan dihitung Rp3.000,00 per iklan. Dalam setiap video terdapat 2 iklan di awal video dan 1 iklan setiap 10 menit video berjalan.
Berapa maksimal waktu jika total pendapatan dalam satu video adalah Rp432.000,00?
Benar
Salah
-
Pertanyaan 12 dari 20
12. Pertanyaan
1 pointsUTBK 2024
Pendapatan seorang youtuber didapat dari iklan yang tayang di setiap video yang dia buat. Pendapatan dari iklan dihitung Rp3.000,00 per iklan. Dalam setiap video terdapat 2 iklan di awal video dan 1 iklan setiap 10 menit video berjalan.
Jika youtuber tersebut membuat video dengan durasi 100 menit, maka pendapatan dari video tersebut sebesar…
Benar
Salah
-
Pertanyaan 13 dari 20
13. Pertanyaan
1 pointsUTBK 2023
Tempat pakan ayam berbentuk balok dengan luas alas \(\left(-x + 20 + \dfrac{300}{x} \right) \text{ cm}^2\) dan tingginya \(x\) cm.
Volume maksimum tempat pakan ayam tersebut adalah… \(\text{ cm}^3\)
Benar
\(\text{Volume} = \text{ luas alas } \times \text{ tinggi}\)
\(\text{V} = \left(-x + 20 + \dfrac{300}{x} \right) \times x\)
\(\text{V} = -x^2 + 20x + 300\)
Agar volume maksimum, maka \(\text{V}’ = 0\)
\(-2x + 20 = 0\)
\(-2x = -20\)
\(x = 10\)
Substitusikan nilai \(x = 10\) ke dalam persamaan volume
\(\text{V}_{\text{max}} = -10^2 + 20(10) + 300\)
\(\text{V}_{\text{max}} = -100 + 200 + 300\)
\(\text{V}_{\text{max}} = 400 \text{ cm}^3\)
Salah
\(\text{Volume} = \text{ luas alas } \times \text{ tinggi}\)
\(\text{V} = \left(-x + 20 + \dfrac{300}{x} \right) \times x\)
\(\text{V} = -x^2 + 20x + 300\)
Agar volume maksimum, maka \(\text{V}’ = 0\)
\(-2x + 20 = 0\)
\(-2x = -20\)
\(x = 10\)
Substitusikan nilai \(x = 10\) ke dalam persamaan volume
\(\text{V}_{\text{max}} = -10^2 + 20(10) + 300\)
\(\text{V}_{\text{max}} = -100 + 200 + 300\)
\(\text{V}_{\text{max}} = 400 \text{ cm}^3\)
-
Pertanyaan 14 dari 20
14. Pertanyaan
1 pointsUTBK 2023
Tempat pakan ayam berbentuk balok dengan luas alas \(\left(-x + 20 + \dfrac{300}{x} \right) \text{ cm}^2\) dan tingginya \(x\) cm.
Jika tempat pakan ayam tersebut diisi setengah dari volume maksimum, maka pakan ayam dalam balok mencapai tinggi… cm
Benar
Volume maksimum terjadi saat \(x = 10\)
Saat tempat pakan ayam diisi setengah dari volume maksimum, maka pakan ayam dalam balok mencapai \(\dfrac{1}{2}x = \dfrac{1}{2}\cdot 10 = 5 \text{ cm}\)
Salah
Volume maksimum terjadi saat \(x = 10\)
Saat tempat pakan ayam diisi setengah dari volume maksimum, maka pakan ayam dalam balok mencapai \(\dfrac{1}{2}x = \dfrac{1}{2}\cdot 10 = 5 \text{ cm}\)
-
Pertanyaan 15 dari 20
15. Pertanyaan
1 pointsUTBK 2023
Persentase waktu yang dihabiskan pegawai dalam satu jabatan (posisi tunggal) di dua industri.
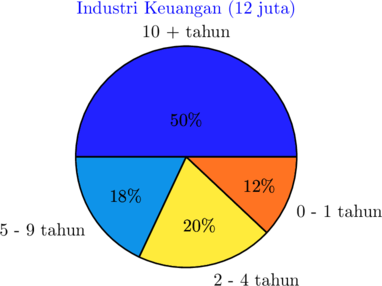
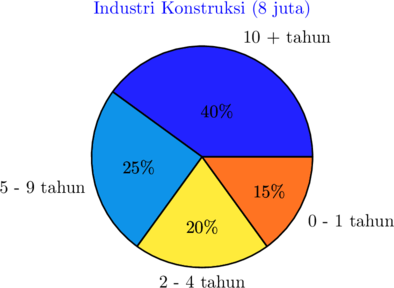
Berdasarkan diagram di atas, untuk pegawai yang bekerja selama 5 sampai 9 tahun di posisi yang sama, berapa besar selisih (dalam derajat) antara bidang konstruksi dengan bidang keuangan?
Benar
Selisih persentase pegawai = 25% − 18% = 7%
Besar selisih = \(\dfrac{7}{100} \times 360^{\circ} = 25^{\circ}\)
Salah
Selisih persentase pegawai = 25% − 18% = 7%
Besar selisih = \(\dfrac{7}{100} \times 360^{\circ} = 25^{\circ}\)
-
Pertanyaan 16 dari 20
16. Pertanyaan
1 pointsUTBK 2023
Persentase waktu yang dihabiskan pegawai dalam satu jabatan (posisi tunggal) di dua industri.


Jika salah satu pegawai di kedua industri tersebut dipilih secara acak, berapa probabilitas pegawai di industri konstruksi yang berada di posisi/jabatan yang sama selama 5 tahun atau lebih?
Benar
Persentase pegawai di industri konstruksi yang bekerja selama 5 tahun atau lebih adalah 25% + 40% = 65%.
Banyak pegawai yang bekerja selama 5 tahun atau lebih:
\(\dfrac{65}{100} \times 8.000.000 = 5.200.000\)
\(n(A) = 5,2 \text{ juta}\)
\(n(S) = 12 \text{ juta } + 8 \text{ juta } = 20 \text{ juta }\)
\(P(A) = \dfrac{n(A) }{n(S) }\)
\(P(A) = \dfrac{5,2 }{20 }= 0,26 \)
\(P(A) = 26\% \)
Salah
Persentase pegawai di industri konstruksi yang bekerja selama 5 tahun atau lebih adalah 25% + 40% = 65%.
Banyak pegawai yang bekerja selama 5 tahun atau lebih:
\(\dfrac{65}{100} \times 8.000.000 = 5.200.000\)
\(n(A) = 5,2 \text{ juta}\)
\(n(S) = 12 \text{ juta } + 8 \text{ juta } = 20 \text{ juta }\)
\(P(A) = \dfrac{n(A) }{n(S) }\)
\(P(A) = \dfrac{5,2 }{20 }= 0,26 \)
\(P(A) = 26\% \)
-
Pertanyaan 17 dari 20
17. Pertanyaan
1 pointsUTBK 2023
Persentase waktu yang dihabiskan pegawai dalam satu jabatan (posisi tunggal) di dua industri.


Perbandingan antara jumlah pegawai industri keuangan yang berada di posisi/jabatan yang sama selama 2 − 9 tahun dengan jumlah pegawai industri konstruksi yang berada di posisi/jabatan yang sama selama 0 − 4 tahun adalah…
Benar
Jumlah pegawai industri keuangan yang berada di posisi yang sama selama 2 – 9 tahun ada sebanyak:
38% × 12 juta = 4,56 juta pegawai
Jumlah pegawai industri konstruksi yang berada di posisi yang sama selama 0 – 4 tahun ada sebanyak:
35% × 8 juta = 2,8 juta pegawai
Perbandiangan antara keduanya adalah 4,56 : 2,8 = 8 : 5
Salah
Jumlah pegawai industri keuangan yang berada di posisi yang sama selama 2 – 9 tahun ada sebanyak:
38% × 12 juta = 4,56 juta pegawai
Jumlah pegawai industri konstruksi yang berada di posisi yang sama selama 0 – 4 tahun ada sebanyak:
35% × 8 juta = 2,8 juta pegawai
Perbandiangan antara keduanya adalah 4,56 : 2,8 = 8 : 5
-
Pertanyaan 18 dari 20
18. Pertanyaan
1 pointsUTBK 2024
Sebuah kolam berbentuk persegi dengan panjang sisi 4 m. Sebuah batu akan dilemparkan tepat di tengah kolam sehingga menimbulkan riak gelombang berbentuk lingkaran. Riak gelombang yang terjadi akan melebar dengan jari-jari bertambah 10 cm tiap detik.
Jika \(R(t)\) menyatakan jari-jari riak gelombang setelah \(t\) detik, maka \(R(t)\) dapat dinyatakan dengan persamaan… (dalam cm).
Benar
\(R(t) = 10t\)
Salah
\(R(t) = 10t\)
-
Pertanyaan 19 dari 20
19. Pertanyaan
1 pointsUTBK 2024
Sebuah kolam berbentuk persegi dengan panjang sisi 4 m. Sebuah batu akan dilemparkan tepat di tengah kolam sehingga menimbulkan riak gelombang berbentuk lingkaran. Riak gelombang yang terjadi akan melebar dengan jari-jari bertambah 10 cm tiap detik.
Luas di dalam lingkaran riak gelombang setelah \(t\) detik dinyatakan dengan \(L(t)\), maka bentuk sistematis dari \(L(t)\) adalah… \(\text{ cm}^2\)
Benar
\(L(t) = \pi \cdot (R(t))^2\)
\(L(t) = \pi \cdot (10t)^2\)
\(L(t) = 100\pi t^2\)
Salah
\(L(t) = \pi \cdot (R(t))^2\)
\(L(t) = \pi \cdot (10t)^2\)
\(L(t) = 100\pi t^2\)
-
Pertanyaan 20 dari 20
20. Pertanyaan
1 pointsUTBK 2024
Sebuah kolam berbentuk persegi dengan panjang sisi 4 m. Sebuah batu akan dilemparkan tepat di tengah kolam sehingga menimbulkan riak gelombang berbentuk lingkaran. Riak gelombang yang terjadi akan melebar dengan jari-jari bertambah 10 cm tiap detik.
Setelah 10 detik riak berjalan, maka luas daerah di luar riak gelombang pertama adalah… \(\text{ cm}^2\)
Benar
Luas daerah yang diarsir = luas kolam − luas lingkaran
Luas daerah yang diarsir = \((400 \times 400) – 100 \pi \cdot 10^2\)
Luas daerah yang diarsir = \(16 \times 10^4 – \:\pi \times 10^4\)
Luas daerah yang diarsir = \((16 – \pi)\cdot 10^4 \text{ cm}^2\)
Salah
Luas daerah yang diarsir = luas kolam − luas lingkaran
Luas daerah yang diarsir = \((400 \times 400) – 100 \pi \cdot 10^2\)
Luas daerah yang diarsir = \(16 \times 10^4 – \:\pi \times 10^4\)
Luas daerah yang diarsir = \((16 – \pi)\cdot 10^4 \text{ cm}^2\)
