Soal 01
Panjang diagonal ruang sebuah kubus tanpa tutup adalah 6 cm. Luas permukaan kubus tersebut adalah…
(A) 60 cm²
(B) 72 cm²
(C) 90 cm²
(D) 108 cm²
Answer: A
Panjang diagonal ruang kubus = \(s\sqrt{3}\)
\(s\sqrt{3} = 6\)
\(s = \dfrac{6}{\sqrt{3}}\)
\(s = \dfrac{6}{\sqrt{3}}\times \color{red} \dfrac{\sqrt{3}}{\sqrt{3}}\)
\(s = 2\sqrt{3}\text{ cm}\)
Panjang sisi kubus = \(2\sqrt{3}\text{ cm}\)
Luas permukaan kubus tanpa tutup = \(5\cdot s^2\)
Luas permukaan kubus tanpa tutup = \(5\cdot (2\sqrt{3})^2\)
Luas permukaan kubus tanpa tutup = \(5\cdot 12 = 60 \text{ cm}^2\)
Soal 02
Dari kawat sepanjang 6 meter akan dibuat 5 buah kerangka kubus identik dengan panjang rusuk 9 cm. Sisa kawatnya adalah…
(A) 20 cm
(B) 40 cm
(C) 60 cm
(D) 80 cm
Answer: C
Kubus memiliki 12 rusuk
Keliling 1 buah kubus = \(12 \times s\)
Keliling 1 buah kubus = \(12 \times 9 = 108 \text{ cm}\)
Keliling 5 buah kubus = \(5 \times 108 = 540\text{ cm}\)
Sisa kawat = \(600 \text{ cm} \:-\: 540 \text{ cm}\)
Sisa kawat = \(60 \text{ cm}\)
Soal 03
Jika volume sebuah kubus sama dengan luas permukaannya, panjang sisi kubus tersebut adalah…
(A) \(5 \text{ cm}\)
(B) \(5\sqrt{2} \text{ cm}\)
(C) \(6 \text{ cm}\)
(D) \(6\sqrt{2} \text{ cm}\)
Answer: C
Volume kubus = luas permukaan kubus
\(s^3 = 6\cdot s^2\)
Bagi kedua ruas dengan \(s^2\)
\(\dfrac{\cancelto{s}{s^3}}{\cancel{s^2}} = \dfrac{6 \cdot \cancel{s^2}}{\cancel{s^2}}\)
\(s = 6 \text{ cm}\)
Soal 04
Sebuah kubus memiliki luas bidang diagonal \(196\sqrt{2} \text{ cm}^2\). Panjang diagonal ruang kubus tersebut adalah…
(A) \(13\sqrt{2} \text{ cm}\)
(B) \(6 \sqrt{3} \text{ cm}\)
(C) \(14\sqrt{2} \text{ cm}\)
(D) \(14\sqrt{3} \text{ cm}\)
Answer: D
Luas bidang diagonal ACGE
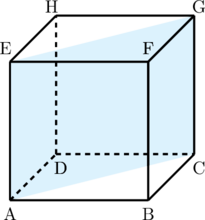
ACGE berbentuk persegi panjang
Luas ACGE = AC × CG
\(196\sqrt{2} = s\sqrt{2} \times s\)
\(196 \cdot \cancel{\sqrt{2}} = s^2 \cdot \cancel{\sqrt{2}}\)
\(s^2 = 196\)
\(s = \sqrt{196}\)
\(s = 14 \text{ cm}\)
Panjang diagonal ruang kubus = \(s\sqrt{3}\)
Panjang diagonal ruang kubus = \(14\sqrt{3} \text{ cm}\)
Soal 05
Sebuah kubus memiliki panjang diagonal sisi \(8\sqrt{2} \text{ cm}\). Volume kubus tersebut adalah…
(A) \(320 \text{ cm}^3\)
(B) \(384 \text{ cm}^3\)
(C) \(512 \text{ cm}^3\)
(D) \(612 \text{ cm}^3\)
Answer: C
Panjang diagonal sisi kubus = \(s\sqrt{2}\)
\(8\cdot \cancel{\sqrt{2}} = s \cdot \cancel{\sqrt{2}}\)
\(s = 8 \text{ cm}\)
Volume kubus = \(s^3\)
Volume kubus = \(8^3 \)
Volume kubus = \(512 \text{ cm}^3 \)
Soal 06
Adi memiliki kotak tempat mainan berbentuk balok tanpa tutup. Kotak tersebut memiliki panjang 30 cm, lebar 15 cm, dan tinggi 10 cm. Luas permukaan kotak tersebut adalah…
(A) \(1.350 \text{ cm}^2\)
(B) \(1.450 \text{ cm}^2\)
(C) \(1.550 \text{ cm}^2\)
(D) \(1.650 \text{ cm}^2\)
Answer: A
Luas permukaan balok tanpa tutup = \(p\cdot l + 2p \cdot t + 2l \cdot t\)
Luas permukaan balok tanpa tutup = \(30\cdot 15 + 2\cdot 30 \cdot 10 + 2\cdot 15 \cdot 10\)
Luas permukaan balok tanpa tutup = \(450 + 600 + 300\)
Luas permukaan balok tanpa tutup = \(1.350 \text{ cm}^2\)
Soal 07
Sebuah prisma alasnya berbentuk belah ketupat dengan panjang diagonal 12 cm dan 16 cm. Jika volume prisma tersebut adalah 1.920 cm³, luas permukaan prisma adalah…
(A) 296 cm²
(B) 392 cm²
(C) 896 cm²
(D) 992 cm²
Answer: D
Volume prisma = luas belah ketupat × tinggi prisma
\(1920 = \dfrac{d_1 \times d_2}{2} \times h\)
\(1920 = \dfrac{12 \times 16}{2} \times h\)
\(1920 = 96 h\)
\(h = \dfrac{1920}{96}\)
\(h = 20 \text{ cm}\)
Tinggi prisma adalah 20 cm
Luas permukaan prisma = (2 × luas belah ketupat) + (keliling belah ketupat × tinggi prisma)
Luas belah ketupat = \(\dfrac{12 \times 16}{2} = 96 \text{ cm}^2\)
Sisi belah ketupat dapat dihitung menggunakan rumus pythagoras.
Kedua diagonal belah ketupat berpotongan secara tegak lurus sehingga membentuk segitiga siku-siku dengan sisi siku-sikunya 6 cm dan 8 cm
Panjang sisi miring = sisi belah ketupat
Panjang sisi miring = \(\sqrt{6^2 + 8^2}\)
Panjang sisi miring = \(\sqrt{100} = 10 \text{ cm}\)
Keliling belah ketupat = 4 × 10 = 40 cm
Luas permukaan prisma = (2 × 96) + (40 × 20)
Luas permukaan prisma = 192 + 800
Luas permukaan prisma = 992 cm²
Soal 08
Sebuah limas T.ABCD alasnya berbentuk persegi dengan panjang sisi 12 cm dan tinggi limas 8 cm.
Tentukan:
(1) Volume limas
(2) Luas permukaan limas
(1) Menentukan volume limas
\(\textbf{Volume limas} = \dfrac{1}{3} \times \textbf{ luas alas } \times \textbf{ tinggi}\)
\(\textbf{Volume limas} = \dfrac{1}{3} \cdot (12\times 12) \cdot 8\)
\(\textbf{Volume limas} = \dfrac{1}{\cancel{3}} \cdot (\cancelto{4}{12}\times 12) \cdot 8\)
\(\textbf{Volume limas} = 384 \text{ cm}^3\)
(2) Menentukan luas permukaan limas
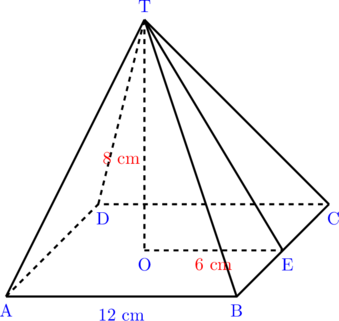
Perhatikan segitiga siku-siku TOE
\(\textbf{TE}^2 = \textbf{TO}^2 + \textbf{OE}^2\)
\(\textbf{TE}^2 = 8^2 + 6^2\)
\(\textbf{TE}^2 = 64 + 36\)
\(\textbf{TE}^2 = 100\)
\(\textbf{TE} = \sqrt{100} =10 \text{ cm}\)
Luas sisi tegak TBC = \(\dfrac{1}{2} \times \textbf{BC} \times \textbf{TE}\)
Luas sisi tegak TBC = \(\dfrac{1}{2} \times 12 \times 10\)
Luas sisi tegak TBC = \(60 \text{ cm}^2\)
\(\textbf{Luas permukaan limas} = \textbf{ luas alas } + 4\cdot \textbf{ luas sisi tegak TBC}\)
\(\textbf{Luas permukaan limas} = (12 \times 12) + 4\cdot (60)\)
\(\textbf{Luas permukaan limas} = 144 + 240\)
\(\textbf{Luas permukaan limas} = 384 \text{ cm}^2\)
Soal 09
Berikut ini adalah gambar prisma trapesium siku-siku.
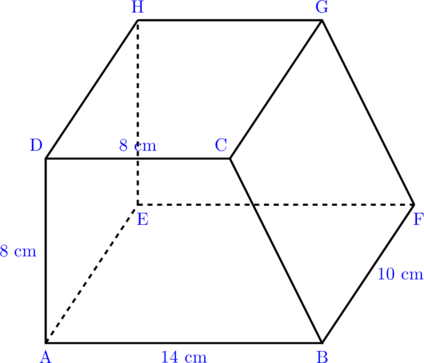
Diketahui AB//DC, panjang AB = 14 cm, DC = 8 cm, AD = 8 cm, dan panjang BF = 10 cm.
Tentukan:
(1) Volume prisma
(2) Panjang BC
(3) Keliling alas prisma
(4) Luas permukaan prisma
(1) Menentukan volume prisma
Volume prisma = luas alas × tinggi prisma
Alas prima adalah trapesium siku-siku ABCD, dengan luas = (jumlah sisi sejajar × tinggi) ÷ 2
\(\textbf{Luas alas} = \dfrac{(\text{AB} + \text{DC}) \times \text {AD}}{2}\)
\(\textbf{Luas alas} = \dfrac{(14 + 8) \times 8}{2}\)
\(\textbf{Luas alas} = 88 \text{ cm}^2\)
Tinggi prisma adalah BF = 10 cm
Volume prisma = luas alas × tinggi prisma
Volume prisma = 88 × 10
Volume prisma = 880 cm²
(2) Menentukan panjang BC
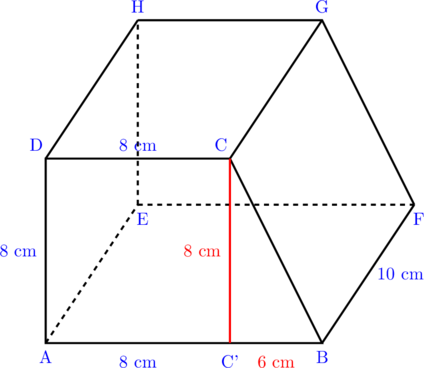
\(\textbf{BC}^2 = \textbf{C’B}^2 + \textbf{CC’}^2\)
\(\textbf{BC}^2 = 6^2 + 8^2\)
\(\textbf{BC}^2 = 36 + 64 =100\)
\(\textbf{BC} = \sqrt{100}\)
\(\textbf{BC} = 10 \text{ cm}\)
(3) Menentukan keliling alas
Keliling alas = AB + BC + CD + AD
Keliling alas = 14 + 10 + 8 + 8
Keliling alas = 40 cm
(4) Menentukan luas permukaan prisma
Luas permukaan prisma = (2 × luas alas) + (keliling alas × tinggi prisma)
Luas permukaan prisma = (2 × 88) + (40 × 10)
Luas permukaan prisma = 176 + 400
Luas permukaan prisma = 576 cm²
Soal 10
Perhatikan gambar berikut.
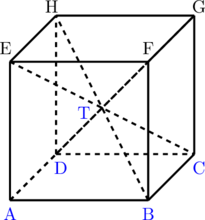
Sebuah kubus ABCD.EFGH memiliki volume 216 cm³. Volume limas T.ABCD yang berada di dalam kubus tersebut adalah…
Kubus ABCD.EFGH terbentuk dari 6 buah limas yang identik dengan limas T.ABCD.
Volume limas T.ABCD = \(\dfrac{1}{6} \times \text{ volume kubus}\)
Volume limas T.ABCD = \(\dfrac{1}{6} \times 216\)
Volume limas T.ABCD = \(36 \text{ cm}^3\)
