Apa Artinya Kongruen?
Bayangkan kamu memiliki dua potongan kertas berbentuk persegi. Jika kamu meletakkan satu di atas yang lain, dan kedua potongan kertas itu pas menutupi satu sama lain, maka kedua potongan kertas itu kongruen.
Dua bangun dikatakan kongruen jika bentuknya sama, ukuran sisinya sama, dan sudut yang bersesuaian sama besar.
Contoh Gambar Bangun yang Kongruen

Selanjutnya, mari kita pelajari kekongruenan pada segitiga.
Dua buah segitiga dikatakan kongruen jika semua sisi dan sudut yang bersesuaian memiliki ukuran yang sama. Artinya, jika kedua segitiga memiliki panjang sisi yang sama dan sudut yang bersesuaian juga sama besar, maka segitiga-segitiga tersebut kongruen.
Berikut ini adalah aturan untuk membuktikan bahwa dua segitiga saling kongruen:
(1) SSS (Sisi, Sisi, Sisi)

Pada gambar di atas, \(\text{AB = PQ}\), \(\text{BC = QR}\), dan \(\text{AC = PR}\), maka \(\triangle \text{ABC} \cong \triangle \text{PQR}\) (dibaca segitiga ABC kongruen dengan segitiga PQR).
(2) SAS (Sisi, Sudut, Sisi)

Pada gambar di atas, \(\text{AB = PQ}\), \(\angle \text{B} = \angle \text{Q} = \beta\), dan \(\text{BC = QR}\), maka \(\triangle \text{ABC} \cong \triangle \text{PQR}\).
(3) ASA (Sudut, Sisi, Sudut)

Pada gambar di atas, \(\angle \text{A} = \angle \text{P} = \alpha\), \(\angle \text{B} = \angle \text{Q} = \beta\), dan \(\text{AB = PQ}\) , maka \(\triangle \text{ABC} \cong \triangle \text{PQR}\).
(4) AAS (Sudut, Sudut, Sisi)
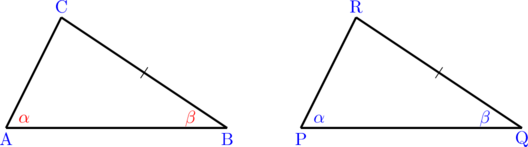
Pada gambar di atas, \(\angle \text{A} = \angle \text{P} = \alpha\), \(\angle \text{B} = \angle \text{Q} = \beta\), dan \(\text{BC = QR}\), maka \(\triangle \text{ABC} \cong \triangle \text{PQR}\).
(5) RHS (Sudut Siku-Siku, Hipotenusa (Sisi Miring), Sebuah Sisi Siku-Siku)

Pada segitiga siku-siku di atas, \(\angle \text{B} = \angle \text{Q} = 90^{\circ}\), \(\text{AC = PR (sisi miring)}\), \(\text{BC = QR}\), maka \(\triangle \text{ABC} \cong \triangle \text{PQR}\).
Catatan:
- Dua buah segitiga yang kongruen sudah pasti sebangun
- Dua buah segitiga yang sebangun belum tentu kongruen
