Soal 01
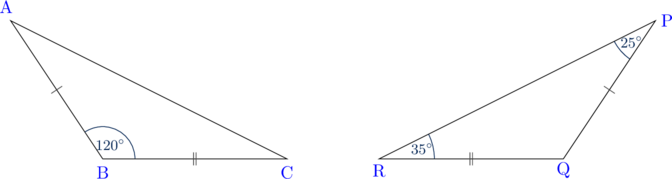
Buktikan bahwa \(\triangle \text{ABC} \cong \triangle \text{PQR}\)
Pada ΔPQR, besar ∠PQR = 180° − 35° − 25° = 120°
(1) AB = PQ (sisi sama panjang)
(2) Besar ∠ABC = ∠PQR = 120° (sudut sama besar)
(3) BC = QR (sisi sama panjang)
Dengan menggunakan aturan SAS (Sisi, Sudut, Sisi), maka ΔABC ≅ ΔPQR.
Soal 02

Buktikan bahwa \(\triangle \text{ABC} \cong \triangle \text{DCB}\)
(1) AB = DC (sisi sama panjang)
(2) Besar ∠ABC = ∠DCB = 160° (sudut sama besar)
(3) BC = BC (sisi yang berhimpit sama panjang)
Dengan menggunakan aturan SAS (Sisi, Sudut, Sisi), maka ΔABC ≅ ΔDCB.
Soal 03
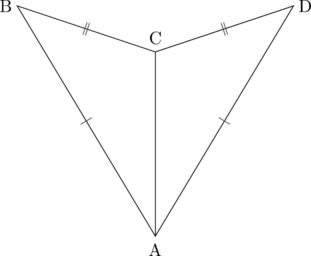
Buktikan bahwa \(\triangle \text{ABC} \cong \triangle \text{ADC}\)
(1) AB = AD (sisi sama panjang)
(2) AC = AC (sisi yang berhimpit sama panjang)
(3) BC = DC (sisi yang berhimpit sama panjang)
Dengan menggunakan aturan SSS (Sisi, Sisi, Sisi), maka ΔABC ≅ ΔADC.
Soal 04
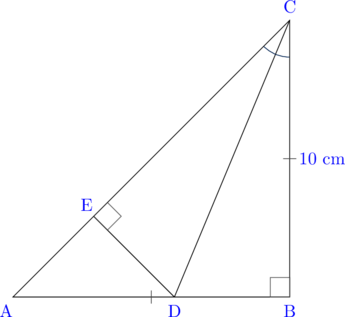
Diketahui panjang AB = BC = 10 cm dan CD bisektor ∠BCA. Tentukan panjang AE.
Akan dibuktikan ΔCBD ≅ ΔCED
(1) Besar ∠DBC = ∠CED = 90° (sudut sama besar)
(2) Besar ∠BCD = ∠ECD (CD membagi ∠BCA menjadi dua sama besar)
(3) CD = CD (sisi yang berhimpit sama panjang)
Dengan menggunakan aturan AAS (Sudut, Sudut, Sisi), maka ΔCBD ≅ ΔCED. Akibatnya panjang CE = CB = 10 cm.
Selanjutnya menentukan panjang AC
Perhatikan segitiga siku-siku sama kaki ABC. Gunakan rumus Pythagoras.
\(\text{AC}^2 = \text{AB}^2 + \text{BC}^2\)
\(\text{AC}^2 = 10^2 + 10^2\)
\(\text{AC}^2 = 100 + 100\)
\(\text{AC}^2 = 200\)
\(\text{AC} = \sqrt{200} = 10\sqrt{2} \text{ cm}\)
Panjang AE = AC − CE
Panjang AE = \(\color{red} (10\sqrt{2}\:-\:10)\text{ cm}\)
Soal 05

ABCD adalah persegi panjang dengan AB = 16 cm dan AD = 12 cm. Tentukan panjang EF.
Akan dibuktikan ΔAED ≅ ΔCFB
(1) Besar ∠AED = ∠CFB= 90° (sudut sama besar)
(2) Besar ∠DAE = ∠BCF (sudut dalam berseberangan sama besar)
(3) AD = CB (sisi yang sama panjang)
Dengan menggunakan aturan AAS (Sudut, Sudut, Sisi), maka ΔAED ≅ ΔCFB. Akibatnya panjang AE = CF.
Misal panjang AE = CF = \(x\) cm.
Menentukan panjang AC
\(\text{AC}^2 = \text{AB}^2 + \text{BC}^2\)
\(\text{AC}^2 = 16^2 + 12^2\)
\(\text{AC}^2 = 256 + 144\)
\(\text{AC}^2 = 400\)
\(\text{AC} = \sqrt{400} = 20 \text{ cm}\)
Perhatikan segitiga siku-siku ADC
\(\text{DA}^2 = \text{AE} \times \text{AC}\)
\(12^2 = x \times 20\)
\(144 = 20x\)
\(x = \dfrac{144}{20}\)
\(x = 7,2 \text{ cm}\)
Panjang EF = AC − 2x
Panjang EF = 20 − 2(7,2)
Panjang EF = 20 − 14,4
Panjang EF = 5,6 cm
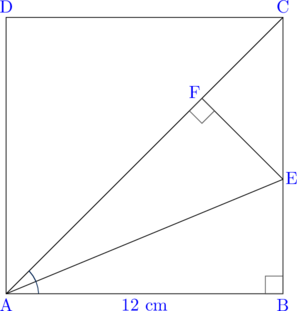
ABCD adalah persegi dengan AB = 12 cm dan AE bisektor ∠BAC. Tentukan panjang CE.
Akan dibuktikan ΔABE ≅ ΔAFE
(1) Besar ∠ABE = ∠AFE = 90° (sudut sama besar)
(2) Besar ∠BAE = ∠FAE (AE membagi ∠BAC menjadi dua sama besar)
(3) AE = AE (sisi yang berhimpit sama panjang)
Dengan menggunakan aturan AAS (Sudut, Sudut, Sisi), maka ΔABE ≅ ΔAFE. Akibatnya panjang AF = AB = 12 cm.
Selanjutnya menentukan panjang AC
Perhatikan segitiga siku-siku sama kaki ABC. Gunakan rumus Pythagoras.
\(\text{AC}^2 = \text{AB}^2 + \text{BC}^2\)
\(\text{AC}^2 = 12^2 + 12^2\)
\(\text{AC}^2 = 144 + 144\)
\(\text{AC}^2 = 2\times 144\)
\(\text{AC} = \sqrt{ 2\times 144} = 12\sqrt{2} \text{ cm}\)
Menentukan panjang CF
CF = AC − AF
CF = \(12\sqrt{2} \:-\: 12\) cm
Perhatikan segitiga siku-siku sama kaki CFE (karena ∠ECF = 45° dan ΔCFE merupakan segitiga siku-siku)
CF = FE = \((12\sqrt{2} \:-\: 12)\) cm
Gunakan rumus Pythagoras untuk menentukan panjang CE
\(\text{CE}^2 = \text{CF}^2 + \text{FE}^2\)
\(\text{CE}^2 = (12\sqrt{2} \:-\: 12)^2 + (12\sqrt{2} \:-\: 12)^2\)
\(\text{CE}^2 = 2(12\sqrt{2} \:-\: 12)^2\)
\(\text{CE} = \sqrt{2(12\sqrt{2} \:-\: 12)^2}\)
\(\text{CE} = (12\sqrt{2}\:-\:12)\sqrt{2}\)
\(\text{CE} = \color{red} (24\:-\:12\sqrt{2}) \text{ cm}\)
