Contoh 01
Gambarkan grafik \(y = 3 \cos \frac{1}{2}x \:-\: 1\) untuk domain \(-2\pi \leq x \leq 2\pi\)
Penyelesaian:
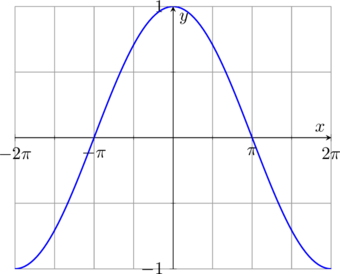
Langkah 1: kita gambar dahulu grafik \(y = \cos \color{red}\frac{1}{2} \color{black}x\)
Periode grafik ini = \(\dfrac{2\pi}{\color{red} \frac{1}{2}} = 4\pi\)
Langkah 2: kita gambar grafik \(y = 3 \cos \frac{1}{2}x\)
Gafik \(y =\color{red}3 \color{black} \cos \frac{1}{2}x\) diperoleh dengan mengalikan semua ordinat (nilai y) pada grafik \(y = \cos \frac{1}{2}x\) dengan 3.
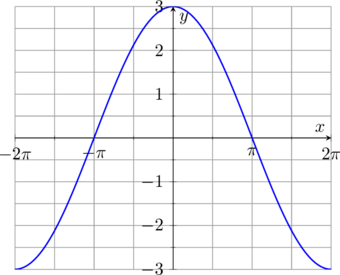
Perhatikan bahwa pada grafik \(y = 3 \cos \frac{1}{2}x\) nilai maksimumnya adalah \(3\) dan nilai minimumnya adalah \(-3\)
Langkah 3: kita gambar grafik \(y = 3 \cos \frac{1}{2}x \:-\: 1\)
Perhatikan bahwa grafik \(y = 3 \cos \frac{1}{2}x \:-\: 1\) diperoleh dengan menggeser grafik \(y = 3 \cos \frac{1}{2}x\) sebesar 1 satuan ke bawah.
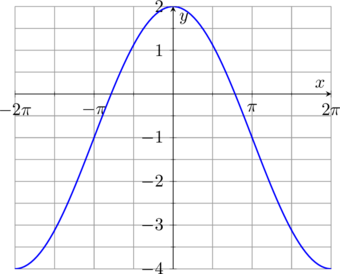
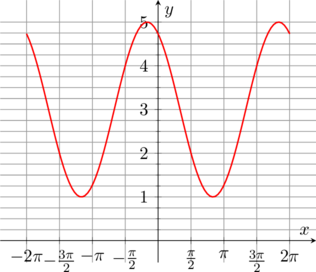
Grafik \(y = 3 \cos \frac{1}{2}x \:-\: 1\) memiliki nilai maksimum \(3 \:-\: 1 = 2\) dan nilai minimum \(-3 \:-\: 1 = -4\)
Jadi, grafik \(y = 3 \cos \frac{1}{2}x \:-\: 1\) untuk domain \(-2\pi \leq x \leq 2\pi\) adalah:
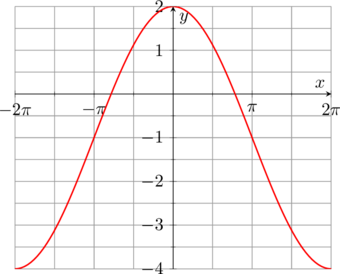
Contoh 02
Gambarkan grafik \(y = 2\cos (x + \frac{\pi}{6}) + 3\) untuk domain \(-2\pi \leq x \leq 2\pi\)
Penyelesaian:
Langkah 1: kita gambar dahulu grafik \(y = \cos(x +\frac{\pi}{6})\)
Periode grafik ini = \(2\pi\)
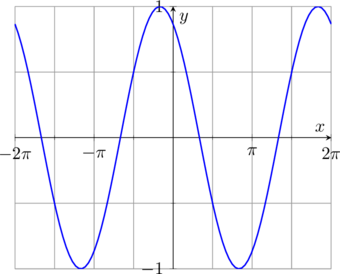
Grafik \(y = \cos (x +\frac{\pi}{6})\) diperoleh dengan menggeser grafik \(y = \cos x\) ke arah kiri sebesar \(\frac{\pi}{6}\).
Langkah 2: kita gambar grafik \(y =2\cos (x +\frac{\pi}{6})\)
Gafik \(y =\color{red}2 \color{black} \cos (x + \frac{\pi}{6})\) diperoleh dengan mengalikan semua ordinat (nilai y) pada grafik \(y = \cos (x + \frac{\pi}{6})\) dengan 2.
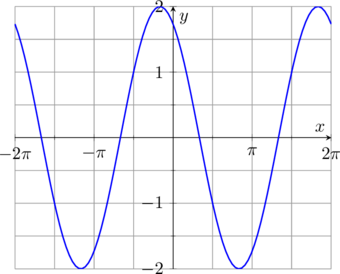
Perhatikan bahwa pada grafik \(y = 2\cos (x +\frac{\pi}{6})\) nilai maksimumnya adalah \(2\) dan nilai minimumnya adalah \(-2\)
Langkah 3: kita gambar grafik \(y = 2\cos (x+\frac{\pi}{6}) + 3\)
Perhatikan bahwa grafik \(y =2\cos (x +\frac{\pi}{6})+ 3\) diperoleh dengan menggeser grafik \(2\cos (x+\frac{\pi}{6})\) sebesar 3 satuan ke atas.
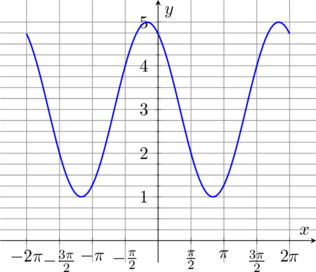
Grafik \(y =2\cos (x+\frac{\pi}{6}) + 3\) memiliki nilai maksimum \(2+ 3 = 5\) dan nilai minimum \(-2 +3 = 1\)
jadi, grafik \(y =2\cos (x+\frac{\pi}{6}) + 3\) untuk domain \(-2\pi \leq x \leq 2\pi\) adalah: