Fungsi \(f(x)\) dan \(g(x)\) dapat dikomposisikan menjadi fungsi baru \(h(x) = (f \circ g)(x) = f(g(x))\) dengan syarat daerah hasil (range) dari \(g(x)\) harus berada di dalam domain \(f(x)\).
Contoh 01
Diketahui \(f(x) = x^2\) dan \(g(x) = x + 1\). Jika \(h(x) = (f \circ g)(x)\), tentukan \(h(3)\).
Domain dari \(f(x) = x^2\) adalah \(\lbrace x|\: x \in \text{ R} \rbrace\:\) (berlaku untuk semua bilangan real).
Range dari \(g(x) = x + 1\) adalah \(\lbrace y|\: y \in \text{ R} \rbrace\:\) (berlaku untuk semua bilangan real juga).
Evaluasi untuk \(x = 3\)
\(g(3) = 3 + 1 = 4\)
Cek apakah hasil dari \(g(3)\) masuk domain \(f(x)\)
- Karena domain \(f(x)\) adalah semua bilangan real, maka 4 termasuk dalam domain \(f(x)\).
- Jadi, 4 valid untuk disubstitusikan ke \(f(x)\)
Langkah perhitungan:
\(h(x) = (f \circ g)(x)\)
\(h(x) = f(g(x))\)
\(h(x) = f(x + 1)\)
Substitusikan \(g(x) = x + 1\) ke dalam \(f(x)\)
\(h(x) = (\color{red} x + 1 \color{gray})^2\)
\(h(3) = (3 + 1)^2\)
\(h(3) = 4^2\)
\(h(3) = 16\)
Contoh 02
Diketahui \(f(x) = \dfrac{x + 1}{x + 2}\) dan \(g(x) = 2x + 3\). Jika \(h(x) = (f \circ g)(x)\), tentukan \(h(0)\).
Domain dari \(f(x) = \dfrac{x + 1}{x + 2}\) adalah \(\lbrace x \in \text{ R}| \: x \neq -2 \rbrace\:\) (berlaku untuk semua bilangan real kecuali −2).
Range dari \(g(x) = 2x + 3\) adalah \(\lbrace y|\: y \in \text{ R} \rbrace\:\) (berlaku untuk semua bilangan real).
Evaluasi untuk \(x = 0\)
\(g(0) = 2(0) + 3 = 3\)
Cek apakah hasil dari \(g(0)\) masuk domain \(f(x)\)
- Karena domain \(f(x)\) adalah semua bilangan real kecuali −2, maka 3 termasuk dalam domain \(f(x)\).
- Jadi, 3 valid untuk disubstitusikan ke \(f(x)\)
Langkah perhitungan:
\(h(x) = (f \circ g)(x)\)
\(h(x) = f(g(x))\)
\(h(x) = f(2x + 3)\)
Substitusikan \(g(x) = 2x +3\) ke dalam \(f(x)\)
\(h(x) = \dfrac{\color{red} 2x + 3 \color{gray} + 1}{\color{red} 2x + 3 \color{gray} + 2}\)
\(h(x) = \dfrac{2x + 4}{2x + 5}\)
\(h(0) = \dfrac{2(0) + 4}{2(0) + 5}\)
\(h(0) = \dfrac{4}{5}\)
Contoh 03
Diketahui \(f(x) = \sqrt{x}\) dan \(g(x) = -x^2\:-\:1\). Apakah \((f \circ g)(x)\) dapat diselesaikan?
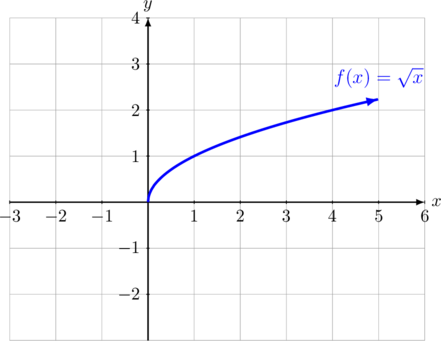
Domain dari \(f(x) = \sqrt{x}\) adalah \(\lbrace x|\: x \geq 0, \: x \in \text{ R} \rbrace\:\) (berlaku untuk semua bilangan real yang lebih besar atau sama dengan nol).
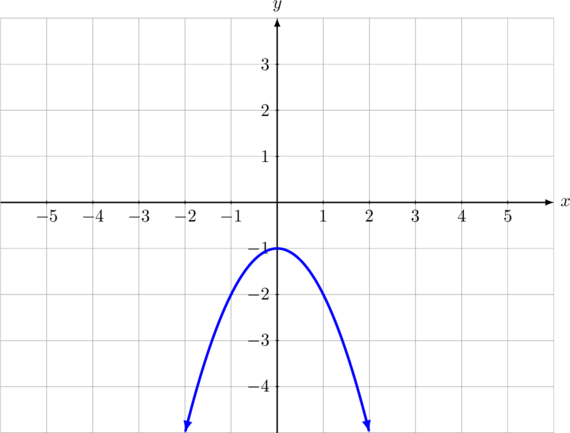
Range dari \(g(x) = -x^2\:-\:1\) adalah \(\lbrace y|\: y \leq -1, \: y \in \text{ R} \rbrace\:\) (berlaku untuk semua bilangan real kurang dari atau sama dengan −1).
Karena output (range) dari \(g(x)\) tidak berada di dalam domain \(f(x)\), maka \((f \circ g)(x)\) tidak dapat diselesaikan.
