Quiz-summary
0 of 14 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
Halo, teman-teman!
Selamat datang di Tryout Pengetahuan Kuantitatif UTBK.
Kalian akan mengerjakan 20 soal PK dalam waktu maksimal 20 menit. Bacalah setiap soal dengan cermat, pahami pertanyaannya, dan pilih jawaban yang paling tepat. Tetap fokus dan percaya diri dalam mengerjakan soal.
Jadikan tryout ini sebagai sarana untuk mengasah kemampuan dan meningkatkan kesiapan kalian menghadapi UTBK.
Selamat mengerjakan, semoga sukses!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 14 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 14
1. Pertanyaan
1 pointsDiketahui bahwa nilai minimum fungsi kuadrat \(g(x)\) adalah −9, dan grafiknya melalui titik (2, 0) dan (6, 0). Grafik fungsi ini juga melalui titik (8, c). Nilai c adalah…
Benar
\(g(x)\) melalui titik (2, 0) dan (6, 0)
\(g(x) = a(x\:-\:x_1)(x\:-\:x_2)\)
\(g(x) = a(x\:-\:2)(x\:-\:6)\)
Sumbu simetri
\(x_p = \dfrac{x_1 + x_2}{2}\)
\(x_p = \dfrac{2 + 6}{2}\)
\(x_p = 4\)
Telah diketahui juga bahwa nilai minimum fungsi adalah \(y_p = -9\)
Substitusikan \((4, -9)\) ke persamaan \(g(x) = a(x\:-\:2)(x\:-\:6)\)
\(-9 = a(4\:-\:2)(4\:-\:6)\)
\(-9 = a(2)(-2)\)
\(-9 = -4a\)
\(a = \dfrac{9}{4}\)
\(g(x) = \dfrac{9}{4}(x\:-\:2)(x\:-\:6)\)
Grafik fungsi ini juga melalui titik (8, c).
Substitusikan titik (8, c) ke \(g(x) = \dfrac{9}{4}(x\:-\:2)(x\:-\:6)\)
\(c = \dfrac{9}{4}(8\:-\:2)(8\:-\:6)\)
\(c = \dfrac{9}{4}(6)(2)\)
\(c = 27\)
Salah
\(g(x)\) melalui titik (2, 0) dan (6, 0)
\(g(x) = a(x\:-\:x_1)(x\:-\:x_2)\)
\(g(x) = a(x\:-\:2)(x\:-\:6)\)
Sumbu simetri
\(x_p = \dfrac{x_1 + x_2}{2}\)
\(x_p = \dfrac{2 + 6}{2}\)
\(x_p = 4\)
Telah diketahui juga bahwa nilai minimum fungsi adalah \(y_p = -9\)
Substitusikan \((4, -9)\) ke persamaan \(g(x) = a(x\:-\:2)(x\:-\:6)\)
\(-9 = a(4\:-\:2)(4\:-\:6)\)
\(-9 = a(2)(-2)\)
\(-9 = -4a\)
\(a = \dfrac{9}{4}\)
\(g(x) = \dfrac{9}{4}(x\:-\:2)(x\:-\:6)\)
Grafik fungsi ini juga melalui titik (8, c).
Substitusikan titik (8, c) ke \(g(x) = \dfrac{9}{4}(x\:-\:2)(x\:-\:6)\)
\(c = \dfrac{9}{4}(8\:-\:2)(8\:-\:6)\)
\(c = \dfrac{9}{4}(6)(2)\)
\(c = 27\)
-
Pertanyaan 2 dari 14
2. Pertanyaan
1 pointsBilangan empat angka \(c385\) kurang dari 7000.
Jika bilangan tersebut dibagi 3 bersisa 2, maka \(c = \dotso\)
Benar
Ambil \(c =1\)
1385 dibagi 3 apakah bersisa 2?
Suatu bilangan habis dibagi 3 jika jumlah semua digitnya merupakan kelipatan 3.
1 + 3 + 8 + 5 = 17
17 dibagi 3 bersisa 2
Jadi, 1385 dibagi 3 akan bersisa 2
Untuk \(c = 1\) bernilai benar
Salah
Ambil \(c =1\)
1385 dibagi 3 apakah bersisa 2?
Suatu bilangan habis dibagi 3 jika jumlah semua digitnya merupakan kelipatan 3.
1 + 3 + 8 + 5 = 17
17 dibagi 3 bersisa 2
Jadi, 1385 dibagi 3 akan bersisa 2
Untuk \(c = 1\) bernilai benar
-
Pertanyaan 3 dari 14
3. Pertanyaan
1 pointsDiketahui kumpulan data berikut:
\(a, -9, 4, -6, b\)
(1) Rata-rata dari kumpulan data tersebut adalah \(-4\) jika \(a = -7\) dan \(b = -4\)
(2) Median dari kumpulan data tersebut adalah \(-7\) jika \(a = -8\) dan \(b = -7\)
(3) Modus dari kumpulan data tersebut adalah \(-6\) jika \(a = -6\) dan \(b = -6\)
(4) Jangkauan dari kumpulan data tersebut adalah \(10\) jika \(a = -10\) dan \(b = 0\)
Pilihan jawaban yang benar adalah…
Benar
(1) Perhitungan rata-rata
Rata-rata = \(\dfrac{-7 + (-9) + 4 + (-6) + (-4)}{5}\)
Rata-rata = \(\dfrac{-22}{5} = -4,4\)
(2) Perhitungan median
Median = nilai tengah dari data terurut (data yang diurutkan dari yang terkecil sampai terbesar)
Median dari data terurut \(-9, -8, -7, -6, 4\) adalah \(-7\)
(3) Perhitungan modus
Modus adalah data yang paling sering muncul
Modus dari data \(-6, -9, 4, -6, -6\) adalah \(-6\)
(4) Perhitungan jangkauan
Jangkauan = data terbesar – data terkecil
Jangkauan dari data \(-10. -9, 4, -6, 0\) adalah \(4\:-\:(-10) = 14\)
Jadi, (2) dan (3) SAJA yang benar.
Salah
(1) Perhitungan rata-rata
Rata-rata = \(\dfrac{-7 + (-9) + 4 + (-6) + (-4)}{5}\)
Rata-rata = \(\dfrac{-22}{5} = -4,4\)
(2) Perhitungan median
Median = nilai tengah dari data terurut (data yang diurutkan dari yang terkecil sampai terbesar)
Median dari data terurut \(-9, -8, -7, -6, 4\) adalah \(-7\)
(3) Perhitungan modus
Modus adalah data yang paling sering muncul
Modus dari data \(-6, -9, 4, -6, -6\) adalah \(-6\)
(4) Perhitungan jangkauan
Jangkauan = data terbesar – data terkecil
Jangkauan dari data \(-10. -9, 4, -6, 0\) adalah \(4\:-\:(-10) = 14\)
Jadi, (2) dan (3) SAJA yang benar.
-
Pertanyaan 4 dari 14
4. Pertanyaan
1 pointsABCD adalah sebuah jajargenjang.
Berdasarkan informasi di atas, berilah tanda √ pada kolom berikut yang sesuai.
Pernyataan Benar Salah ABCD mempunyai dua pasang sudut berhadapan sama besar. ABCD mempunyai dua pasang sisi sama panjang. Kedua diagonal ABCD sama panjang. Pilihan jawaban:
Benar
Dalam jajargenjang:
- Sudut yang berhadapan selalu sama besar.
- Sisi yang berhadapan memiliki panjang yang sama.
- Diagonal suatu jajargenjang bisa tidak sama panjang, tetapi saling membagi dua bagian yang sama besar.
Salah
Dalam jajargenjang:
- Sudut yang berhadapan selalu sama besar.
- Sisi yang berhadapan memiliki panjang yang sama.
- Diagonal suatu jajargenjang bisa tidak sama panjang, tetapi saling membagi dua bagian yang sama besar.
-
Pertanyaan 5 dari 14
5. Pertanyaan
1 pointsLima bilangan asli berbeda yang kurang dari 12 dipilih secara acak. Berapakah banyaknya dari empat pernyataan berikut yang bernilai benar berdasarkan informasi di atas?
(1) Peluang semua bilangan yang terpilih adalah bilangan prima kurang dari \(\dfrac{1}{15}\).
(2) Peluang semua bilangan yang terpilih adalah bilangan genap lebih dari \(\dfrac{1}{10}\).
(3) Peluang semua bilangan yang terpilih adalah bilangan ganjil kurang dari \(\dfrac{1}{5}\).
(4) Peluang jumlah semua bilangan yang terpilih lebih dari 44 adalah \(\dfrac{1}{231}\).
Pilihan jawaban:
Benar
Bilangan asli kurang dari 12
\(S = \lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 \rbrace\)
Banyak cara memilih 5 bilangan dari 11
\(n(S) = \:^{11}\text{C}_{5} = 462\)
Pernyataan (1)
Bilangan prima kurang dari 12: {2, 3, 5, 7, 11}
\(n(A) = \:^5\text{C}_5 = 1\)
\(P(A) = \dfrac{n(A)}{n(S)}\)
\(P(A) = \dfrac{1}{463}\)
\(\dfrac{1}{462} < \dfrac{1}{15}\) BENAR
Pernyataan (2)
Bilangan genap kurang dari 12: {2, 4, 6, 8, 10}
\(n(B) =\: ^5\text{C}_5 = 1\)
\(P(B) = \dfrac{n(B)}{n(S)}\)
\(P(B) = \dfrac{1}{463}\)
\(\dfrac{1}{462} < \dfrac{1}{10}\) SALAH
Pernyataan (3)
Bilangan ganjil kurang dari 12: {1, 3, 5, 7, 9, 11}
Banyak cara memilih 5 bilangan dari 6:
\(n(C) = \:^6\text{C}_5 = 6\)
\(P(C) = \dfrac{n(C) }{n(S) }\)
\(P(C) = \dfrac{6}{462}\)
\(P(C) = \dfrac{1}{77}\)
\(\dfrac{1}{77} < \dfrac{1}{5}\) BENAR
Pernyataan (4)
Kombinasi 5 bilangan yang jumlahnya lebih dari 44:
(7, 8, 9, 10, 11) Jumlah = 45 (memenuhi)
(6, 8, 9, 10, 11) Jumlah = 44 (tidak memenuhi)
Jadi hanya ada 1 kombinasi 5 bilangan yang jumlahnya lebih dari 44.
\(P(D) = \dfrac{1}{462}\) SALAH
Salah
Bilangan asli kurang dari 12
\(S = \lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 \rbrace\)
Banyak cara memilih 5 bilangan dari 11
\(n(S) = \:^{11}\text{C}_{5} = 462\)
Pernyataan (1)
Bilangan prima kurang dari 12: {2, 3, 5, 7, 11}
\(n(A) = \:^5\text{C}_5 = 1\)
\(P(A) = \dfrac{n(A)}{n(S)}\)
\(P(A) = \dfrac{1}{463}\)
\(\dfrac{1}{462} < \dfrac{1}{15}\) BENAR
Pernyataan (2)
Bilangan genap kurang dari 12: {2, 4, 6, 8, 10}
\(n(B) =\: ^5\text{C}_5 = 1\)
\(P(B) = \dfrac{n(B)}{n(S)}\)
\(P(B) = \dfrac{1}{463}\)
\(\dfrac{1}{462} < \dfrac{1}{10}\) SALAH
Pernyataan (3)
Bilangan ganjil kurang dari 12: {1, 3, 5, 7, 9, 11}
Banyak cara memilih 5 bilangan dari 6:
\(n(C) = \:^6\text{C}_5 = 6\)
\(P(C) = \dfrac{n(C) }{n(S) }\)
\(P(C) = \dfrac{6}{462}\)
\(P(C) = \dfrac{1}{77}\)
\(\dfrac{1}{77} < \dfrac{1}{5}\) BENAR
Pernyataan (4)
Kombinasi 5 bilangan yang jumlahnya lebih dari 44:
(7, 8, 9, 10, 11) Jumlah = 45 (memenuhi)
(6, 8, 9, 10, 11) Jumlah = 44 (tidak memenuhi)
Jadi hanya ada 1 kombinasi 5 bilangan yang jumlahnya lebih dari 44.
\(P(D) = \dfrac{1}{462}\) SALAH
-
Pertanyaan 6 dari 14
6. Pertanyaan
1 pointsSegitiga \(XYZ\) adalah segitiga siku-siku dengan \(\angle X\:-\:\angle Y = 30^{\circ}\) dan \(\angle Z = b^{\circ}\).
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas \(P\) dan \(Q\) berikut yang benar?
P Q \(b\) \(70\) Benar
Tidak dapat ditentukan hubungan P dan Q
Salah
Tidak dapat ditentukan hubungan P dan Q
-
Pertanyaan 7 dari 14
7. Pertanyaan
1 pointsDiketahui barisan bilangan real 3, b, 11, …
Apakah 23 merupakan salah satu suku barisan tersebut?
Putuskan apakah pernyataan berikut cukup untuk menjawab pertanyaan tersebut.
- Barisan tersebut adalah barisan aritmetika.
- Barisan tersebut terdiri dari bilangan ganjil positif.
Benar
Pernyataan 1: barisan tersebut adalah barisan aritmetika.
Barisan aritmetika memiliki beda tetap/konstan.
3, b, 11, …
\(b\:-\:3 = 11 \:-\:b\)
\(2b = 14\)
\(b = 7\)
Barisan aritmetika: 3, 7, 11, 15, 19, 23, …
23 merupakan salah satu suku barisan ini (terbukti)
Pernyataan 2: barisan tersebut terdiri dari bilangan ganjil positif.
Namun, ini tidak cukup untuk menentukan pola barisan secara pasti, karena banyak barisan yang memenuhi kriteria ini (misalnya barisan bilangan prima ganjil atau barisan geometri dengan suku-suku ganjil). Oleh karena itu, pernyataan (2) tidak cukup.
Kesimpulan:
Pernyataan (1) saja sudah cukup, tetapi pernyataan (2) saja tidak cukup.
Jawaban yang benar adalah (A).Salah
Pernyataan 1: barisan tersebut adalah barisan aritmetika.
Barisan aritmetika memiliki beda tetap/konstan.
3, b, 11, …
\(b\:-\:3 = 11 \:-\:b\)
\(2b = 14\)
\(b = 7\)
Barisan aritmetika: 3, 7, 11, 15, 19, 23, …
23 merupakan salah satu suku barisan ini (terbukti)
Pernyataan 2: barisan tersebut terdiri dari bilangan ganjil positif.
Namun, ini tidak cukup untuk menentukan pola barisan secara pasti, karena banyak barisan yang memenuhi kriteria ini (misalnya barisan bilangan prima ganjil atau barisan geometri dengan suku-suku ganjil). Oleh karena itu, pernyataan (2) tidak cukup.
Kesimpulan:
Pernyataan (1) saja sudah cukup, tetapi pernyataan (2) saja tidak cukup.
Jawaban yang benar adalah (A). -
Pertanyaan 8 dari 14
8. Pertanyaan
1 pointsDiketahui fungsi \(g\) didefinisikan sebagai
\(g(x) = x^2 + 2x\)
Nilai dari \(\dfrac{g(g(g(1)))}{g(g(1))}\:-\:g(1)\) adalah…
Benar
Langkah 1: Hitung \(g(1)\)
\(g(1) = 1^2 + 2(1) = 3\)
Langkah 2: Hitung \(g(g(1)) = g(3)\)
\(g(3) = 3^2 + 2(3) = 15\)
Langkah 3: Hitung \(g(g(g(1)))\) = g(15)\)
\(g(15) = 15^2 + 2(15) = 255\)
Langkah 4: Hitung hasil akhir
\(\dfrac{g(g(g(1)))}{g(g(1))}\:-\:g(1) = \dfrac{255}{15}\:-\:3\)
\(17\:-\:3 = 14\)
Salah
Langkah 1: Hitung \(g(1)\)
\(g(1) = 1^2 + 2(1) = 3\)
Langkah 2: Hitung \(g(g(1)) = g(3)\)
\(g(3) = 3^2 + 2(3) = 15\)
Langkah 3: Hitung \(g(g(g(1)))\) = g(15)\)
\(g(15) = 15^2 + 2(15) = 255\)
Langkah 4: Hitung hasil akhir
\(\dfrac{g(g(g(1)))}{g(g(1))}\:-\:g(1) = \dfrac{255}{15}\:-\:3\)
\(17\:-\:3 = 14\)
-
Pertanyaan 9 dari 14
9. Pertanyaan
1 pointsSebuah persegi panjang besar dengan luas 48 cm² tersusun atas 4 buah persegi dan 2 buah persegi panjang kecil. Tiga buah persegi diketahui luasnya seperti dalam gambar berikut.
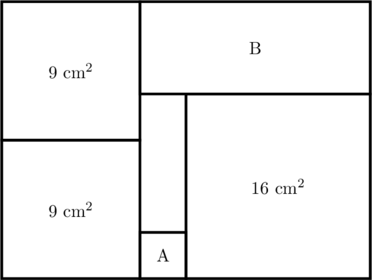
Berdasarkan gambar, tentukan perbandingan luas persegi A dan persegi panjang B dalam persegi panjang besar.
Benar
Misal luas persegi A = \(x^2\)
Ukuran persegi panjang besar
Panjang = \(7 + x\) cm
Lebar = \(6\) cm
Luas persegi panjang besar = 48 cm²
\((7 + x)(6) = 48\)
\(42 + 6x = 48\)
\(6x = 6\)
\(x = 1\)
Luas persegi A = 1 cm²
Ukuran persegi panjang B
Panjang = \(4 + x = 4 + 1 = 5\) cm
Lebar = 2 cm
Luas persegi panjang B = \(5 \times 2 = 10\) cm²
Perbandingan luas persegi A dengan persegi panjang B = 1 : 10
Salah
Misal luas persegi A = \(x^2\)
Ukuran persegi panjang besar
Panjang = \(7 + x\) cm
Lebar = \(6\) cm
Luas persegi panjang besar = 48 cm²
\((7 + x)(6) = 48\)
\(42 + 6x = 48\)
\(6x = 6\)
\(x = 1\)
Luas persegi A = 1 cm²
Ukuran persegi panjang B
Panjang = \(4 + x = 4 + 1 = 5\) cm
Lebar = 2 cm
Luas persegi panjang B = \(5 \times 2 = 10\) cm²
Perbandingan luas persegi A dengan persegi panjang B = 1 : 10
-
Pertanyaan 10 dari 14
10. Pertanyaan
1 pointsSebuah laptop mendapatkan diskon dua kali berturut-turut, yaitu 25% dan \(y\)%. Jika total diskon yang diberikan adalah 40%, maka nilai \(y\) adalah…
Benar
Bisa gunakan rumus:
\(D_{\text{total}} = a + b \:-\:\dfrac{a \cdot b}{100}\)
dengan:
\(D_{\text{total}}\) = total diskon yang diberikan
\(a\) = diskon pertama (dalam persen)
\(b\) = diskon kedua (dalam persen)
\(40 = 25 + y \:-\: \dfrac{25 \cdot y}{100}\)
Kalikan kedua ruas dengan 100
\(4000 = 2500 + 100y \:-\:25y\)
\(4000 = 2500 + 75y\)
\(1500 = 75y\)
\(y = \dfrac{1500}{75}\)
\(y = 20\)
Salah
Bisa gunakan rumus:
\(D_{\text{total}} = a + b \:-\:\dfrac{a \cdot b}{100}\)
dengan:
\(D_{\text{total}}\) = total diskon yang diberikan
\(a\) = diskon pertama (dalam persen)
\(b\) = diskon kedua (dalam persen)
\(40 = 25 + y \:-\: \dfrac{25 \cdot y}{100}\)
Kalikan kedua ruas dengan 100
\(4000 = 2500 + 100y \:-\:25y\)
\(4000 = 2500 + 75y\)
\(1500 = 75y\)
\(y = \dfrac{1500}{75}\)
\(y = 20\)
-
Pertanyaan 11 dari 14
11. Pertanyaan
1 pointsSeorang pengemudi mobil biasanya menempuh perjalanan sejauh 36 km ke kantornya dalam waktu 45 menit. Pada suatu hari, ia berangkat terlambat 9 menit. Dengan kecepatan berapa ia harus berkendara agar sampai pada waktu yang sama seperti biasanya?
Benar
Langkah 1: Tentukan waktu yang tersisa
Waktu tempuh biasa = 45 menit
Waktu tersisa setelah terlambat = 45 − 9 = 36 menit = 0,6 jam
Langkah 2: Gunakan rumus kecepatan
\(s = v \times t\)
\(36 = v \times 0,6\)
\(v = \dfrac{36}{0,6}\)
\(v = 60 \text{ km/jam}\)
Salah
Langkah 1: Tentukan waktu yang tersisa
Waktu tempuh biasa = 45 menit
Waktu tersisa setelah terlambat = 45 − 9 = 36 menit = 0,6 jam
Langkah 2: Gunakan rumus kecepatan
\(s = v \times t\)
\(36 = v \times 0,6\)
\(v = \dfrac{36}{0,6}\)
\(v = 60 \text{ km/jam}\)
-
Pertanyaan 12 dari 14
12. Pertanyaan
1 pointsDiketahui:
\(q = 5 + 2\sqrt{6}\)
Tentukan nilai dari \(5\:-\:2\sqrt{6}\) dalam bentuk yang paling sederhana.
Benar
Gunakan konsep perkalian konjugat
Perhatikan bahwa \(5\:-\:2\sqrt{6}\) adalah konjugat dari \(5 + 2\sqrt{6}\).
\(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}}\)
\(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}} \times \color{red} \dfrac{5\:-\:2\sqrt{6}}{5\:-\:2\sqrt{6}}\)
\(5\:-\:2\sqrt{6} = \dfrac{5\:-\:2\sqrt{6}}{25\:-\:24}\)
\(5\:-\:2\sqrt{6} = 5\:-\:2\sqrt{6}\) sama!
Jadi, \(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}}= \dfrac{1}{p}\)
Salah
Gunakan konsep perkalian konjugat
Perhatikan bahwa \(5\:-\:2\sqrt{6}\) adalah konjugat dari \(5 + 2\sqrt{6}\).
\(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}}\)
\(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}} \times \color{red} \dfrac{5\:-\:2\sqrt{6}}{5\:-\:2\sqrt{6}}\)
\(5\:-\:2\sqrt{6} = \dfrac{5\:-\:2\sqrt{6}}{25\:-\:24}\)
\(5\:-\:2\sqrt{6} = 5\:-\:2\sqrt{6}\) sama!
Jadi, \(5\:-\:2\sqrt{6} = \dfrac{1}{5 + 2\sqrt{6}}= \dfrac{1}{p}\)
-
Pertanyaan 13 dari 14
13. Pertanyaan
1 pointsNilai dari bentuk \(\left( \dfrac{8^3}{2^{-1} \times 16}\right)^{\dfrac{1}{3}} \) adalah…
Benar
\(\left( \dfrac{(2^3)^3}{2^{-1} \times 16}\right)^{\dfrac{1}{3}} \)
\(\left( \dfrac{2^9}{\dfrac{1}{\cancel{2}} \times \cancelto{8}{16}}\right)^{\dfrac{1}{3}} \)
\(\left( \dfrac{2^9}{2^3}\right)^{\dfrac{1}{3}}\)
\(\dfrac{2^3}{2^1}\)
\(2^{3\:-\:1}\)
\(2^2 = 4\)
Salah
\(\left( \dfrac{(2^3)^3}{2^{-1} \times 16}\right)^{\dfrac{1}{3}} \)
\(\left( \dfrac{2^9}{\dfrac{1}{\cancel{2}} \times \cancelto{8}{16}}\right)^{\dfrac{1}{3}} \)
\(\left( \dfrac{2^9}{2^3}\right)^{\dfrac{1}{3}}\)
\(\dfrac{2^3}{2^1}\)
\(2^{3\:-\:1}\)
\(2^2 = 4\)
-
Pertanyaan 14 dari 14
14. Pertanyaan
1 pointsPada segitiga siku-siku ACB, siku-siku di C, diketahui nilai \(\cos A = \dfrac{3}{5}\). Manakah dari keempat pernyataan berikut yang benar?
(1) \(\sin^2 A = \dfrac{16}{25}\)
(2) \(\tan^2A = \dfrac{9}{16}\)
(3) \(\sin^2B = \dfrac{9}{25}\)
(4) \(\cos^2 B = \dfrac{16}{25}\)
Benar
Salah
