Perhatikan ilustrasi berikut.
Pada pukul 08.10 Arum mengendarai sepeda ke rumah Santi dengan kecepatan rata-rata 8 km/jam. Pada saat yang sama, Santi mengendarai sepeda ke rumah Arum dengan kecepatan rata-rata 10 km/jam. Tiga menit kemudian mereka berpapasan.
(1) Jarak antara rumah Arum dan Santi adalah 0,9 km.
(2) Mereka berdua berpapasan pukul 08.13.
(3) Jarak yang ditempuh Santi saat berpapasan adalah 0,2 km.
(4) Jarak yang ditempuh Arum saat berpapasan adalah 0,3 km.
(5) Selisih jarak tempuh saat mereka berpapasan adalah 0,1 km.
Jawaban: C
\(s = \text{jarak yang ditempuh}\)
\(v = \text{kecepatan}\)
\(t = \text{waktu tempuh}\)
\(\color{blue} s = v \times t\)
(A) Menentukan jarak antara Rumah Arum dan Santi
Jarak antara rumah Arum dan Santi dapat dihitung dengan menjumlahkan jarak rumah Arum sampai titik mereka berpapasan (\(s_{\text{Arum}}\)) dengan jarak rumah Santi sampai titik mereka berpapasan (\(s_{\text{Santi}}\)).
Waktu mereka berpapasan \(t = 3 \text{ menit} = \dfrac{3}{60} \text{ jam} = \dfrac{1}{20} \text{ jam}\)
\(\text{Jarak rumah} = s_{\text{Arum}} + s_{\text{Santi}}\)
\(\text{Jarak rumah} = v_1 \cdot t + v_2 \cdot t\)
\(\text{Jarak rumah} = 8 \cdot \dfrac{1}{20} + 10 \cdot \dfrac{1}{20}\)
\(\text{Jarak rumah} = \dfrac{8}{20} + \dfrac{10}{20}\)
\(\text{Jarak rumah} = \dfrac{18}{20}\)
\(\text{Jarak rumah} = \dfrac{9}{10}\)
\(\text{Jarak rumah} = 0,9 \text{ km}\)
Jadi, jarak antara rumah Arum dan Santi adalah 0,9 km.
(B) Menentukan waktu mereka berdua berpapasan
Mereka berdua berangkat dari rumah masing-masing Pk 08.10 dan berpapasan 3 menit kemudian
Jadi, mereka berdua berpapasan pada Pk 08.13
(C) Menentukan jarak yang ditempuh Santi saat berpapasan
\( s_{\text{Santi}} = v_2 \cdot t\)
\( s_{\text{Santi}} = 10 \cdot \dfrac{1}{20}\)
\( s_{\text{Santi}} = \dfrac{10}{20}\)
\( s_{\text{Santi}} = 0,5 \text{ km}\)
Jadi, jarak yang ditempuh Santi saat berpapasan adalah 0,5 km.
(D) Menentukan jarak yang ditempuh Arum saat berpapasan
\( s_{\text{Arum}} = v_1 \cdot t\)
\( s_{\text{Arum}} = 8 \cdot \dfrac{1}{20}\)
\( s_{\text{Arum}} = \dfrac{8}{20}\)
\( s_{\text{Arum}} = \dfrac{2}{5}\)
\( s_{\text{Arum}} = 0,4 \text{ km}\)
Jadi, jarak yang ditempuh Arum saat berpapasan adalah 0,4 km.
(E) Menentukan selisih jarak tempuh saat mereka berpapasan
Selisih jarak tempuh saat mereka berpapasan = 0,5 km − 0,4 km = 0,1 km
Jarak rumah Erwin dan Andra adalah 60 km, Erwin berkendara dari rumahnya menuju rumah Andra pada pukul 09.10 WIB dengan kecepatan rata-rata 60 km/jam. Pada pukul 09.25 WIB Andra berkendara menuju rumah Erwin dengan kecepatan 40 km/jam. Mereka melalui jalan lurus yang sama tanpa hambatan. Mereka akan berpapasan pada pukul…
Jawaban: C
Erwin berangkat dari rumahnya pada pukul 09.10 WIB sedangkan Andra berangkat dari rumahnya pada pukul 09.25 WIB. Selisih waktu keberangkatan mereka adalah 15 menit = 1/4 jam.
Misal waktu yang dibutuhkan Erwin (yang duluan berangkat) sampai mereka berpapasan adalah \(t\) jam, maka waktu yang dibutuhkan Andra (yang berangkat terakhir) sampai mereka berpapasan adalah \((t\:-\:\dfrac{1}{4})\) jam.
Jarak = kecepatan × waktu
Jarak rumah Erwin dan Andra = Jarak Erwin sampai mereka berpapasan + Jarak Andra sampai mereka berpapasan
\(60 \text{ km} = 60 \cdot t + \left(40 \cdot \left(t\:-\:\dfrac{1}{4}\right)\right)\)
\(60 = 60t + 40t\:-\: \left(40 \times \dfrac{1}{4}\right)\)
\(60 = 60t + 40t\:-\: 10\)
\(60 = 100t\:-\: 10\)
\(60 + 10 = 100t\)
\(70 = 100t\)
Bagi kedua ruas dengan 100
\(t = \dfrac{70}{100} = \dfrac{7}{10}\text{ jam}\)
Jadi, waktu yang dibutuhkan Erwin sampai mereka berpapasan adalah \(\dfrac{7}{10}\text{ jam} = \dfrac{7}{10} \times 60 \text{ menit} = 42 \text{ menit}\), sedangkan Andra membutuhkan waktu \(\left(\dfrac{7}{10}\:-\:\dfrac{1}{4}\right)\text{ jam} = \dfrac{9}{20} \text{ jam} =\dfrac{9}{20}\times 60 \text{ menit} = 27 \text{ menit} \)
Dihitung dari waktu Erwin berangkat, mereka akan berpapasan pada pukul 09.10 + 42 = 09.52 WIB,
atau boleh juga dihitung dari waktu Andra berangkat 09.25 + 27 = 09.52 WIB.
Jarak kota Jogja-Sleman 39 km. Dora mengendarai sepeda dari Jogja ke Sleman. Ia berangkat pukul 07.15 dengan kecepatan rata-rata 12 km/jam. Emon mengendarai sepeda dari Sleman – Jogja. Ia berangkat pukul 07.35 dengan kecepatan rata-rata 16 km/jam. Mereka berkendara melalui jalan yang sama. Mereka berpapasan pada pukul…
Jawaban: B
Dora berangkat dari rumahnya pada pukul 07.15 WIB sedangkan Emon berangkat dari rumahnya pada pukul 07.35 WIB. Selisih waktu keberangkatan mereka adalah 20 menit = 1/3 jam.
Misal waktu yang dibutuhkan Dora (yang duluan berangkat) sampai mereka berpapasan adalah \(t\) jam, maka waktu yang dibutuhkan Emon (yang berangkat terakhir) sampai mereka berpapasan adalah \((t\:-\:\dfrac{1}{3})\) jam.
Jarak = kecepatan × waktu
Jarak kota Jogja-Sleman = Jarak Dora sampai mereka berpapasan + Jarak Emon sampai mereka berpapasan
\(39 \text{ km} = 12 \cdot t+ \left(16 \cdot \left(t\:-\:\dfrac{1}{3}\right)\right)\)
\(39 = 12t + 16t\:-\: \left(16 \times \dfrac{1}{3}\right)\)
\(39 = 28t\:-\: \dfrac{16}{3}\)
\(39 + \dfrac{16}{3} = 28t\)
\(\dfrac{133}{3} = 28t\)
Bagi kedua ruas dengan 28
\(t = \dfrac{133}{84} = \dfrac{19}{12}\text{ jam}\)
Jadi, waktu yang dibutuhkan Dora sampai mereka berpapasan adalah \(\dfrac{19}{12}\text{ jam} = \dfrac{19}{12} \times 60 \text{ menit} = 95 \text{ menit}\), sedangkan Emon membutuhkan waktu \(\left(\dfrac{19}{12}\:-\:\dfrac{1}{3}\right)\text{ jam} = \dfrac{5}{4} \text{ jam} =\dfrac{5}{4}\times 60 \text{ menit} = 75 \text{ menit} \)
Dihitung dari waktu Dora berangkat, mereka akan berpapasan pada pukul 07.15 + 95 = Pk 08.50,
atau boleh juga dihitung dari waktu Andra berangkat 07.35 + 75 = Pk 08.50.
Perhatikan gambar berikut.
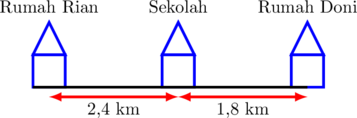
Rian berangkat ke sekolah pukul 06.22, sedangkan Doni berangkat pukul 06.28. Mereka berdua berangkat dengan menggunakan sepeda. Kecepatan rata-rata Rian bersepeda 12 km/jam. Mereka sepakat tiba di sekolah dalam waktu bersamaan. Berdasarkan ilustrasi tersebut perhatikan pernyataan berikut!
(5) Kecepatan Doni lebih tinggi daripada kecepatan Rian.
(6) Kecepatan Rian lebih tinggi daripada kecepatan Doni.
Jawaban: C
Langkah 1: Menghitung waktu perjalanan Rian sampai ke sekolah
\(\color {blue} s = v \cdot t\)
\(2,4 \text{ km} = 12 \text{ km/jam} \cdot t\)
\(t = \dfrac{2,4}{12}\text{ jam}\)
\(t = \dfrac{2,4}{12} \times 60 \text{ menit}\)
\(t = 12 \text{ menit}\)
Rian tiba di sekolah pada pukul 06.22 + 12 = Pk 06.34
Langkah 2: Menghitung kecepatan rata-rata Doni
Doni berangkat ke sekolah pada pukul 06.28
Doni tiba di sekolah pukul 06.34 (sama dengan Rian)
Waktu perjalanan Doni untuk sampai ke sekolah = 06.34 − 06.28 = 6 menit
\(6 \text{ menit} = \dfrac{6}{60} \text{ jam} = \dfrac{1}{10} \text{ jam}\)
\(\color {blue} s = v \cdot t\)
\(1,8 \text{ km} = v \cdot \dfrac{1}{10} \text{ jam}\)
Kalikan kedua ruas dengan 10
\(v = 18 \text{ km/jam}\)
Jadi, kecepatan rata-rata Doni bersepeda adalah 18 km/jam
Kecepatan rata-rata Doni bersepeda lebih tinggi daripada Rian.
Kesimpulan:
Pernyataan yang benar adalah pernyataan nomor (2), (3), dan (5)
