Soal 01
Seorang petani memiliki dua ladang yang akan ditanami kembali setelah panen. Ladang pertama dipanen setiap 18 hari sekali, sedangkan ladang kedua setiap 24 hari sekali. Jika pada tanggal 5 Maret 2025 kedua ladang dipanen bersamaan, pada tanggal berapa kedua ladang akan dipanen bersamaan lagi untuk KETIGA kalinya setelah 5 Maret 2025?
(A) 26 Juli 2025
(B) 27 Juli 2025
(C) 28 Juli 2025
(D) 29 Juli 2025
Jawaban: B
Soal cerita di atas dapat kita selesaikan dengan menghitung KPK dari 18 dan 24.
Faktorisasi prima dari 18 adalah 2 × 3²
Faktorisasi prima dari 24 adalah 2³ × 3
KPK dari 18 dan 24 pilih faktor prima dengan pangkat tertinggi
KPK dari 18 dan 24 = 2³ × 3²
KPK dari 18 dan 24 = 8 × 9 = 72
Kedua ladang akan dipanen bersama setiap 72 hari sekali.
Sekarang, hitung tanggal panen:
- Panen ke-1: 5 Maret 2025
- Panen ke-2: 5 Maret + 72 hari = 16 Mei
- Panen ke-3: 16 Mei + 72 hari = 27 Juli
Jadi, kedua ladang akan dipanen bersamaan lagi untuk KETIGA kalinya pada tanggal 27 Juli 2025.
Note:
Ingat bahwa bulan Maret ada 31 hari, April ada 30 hari, Mei ada 31 hari, Juni ada 30 hari, dan Juli ada 31 hari.
Soal 02
Sebuah kolam renang berbentuk persegi panjang memiliki panjang 25 m dan lebar 15 m. Di sekeliling kolam akan dibuat jalan setapak dengan lebar 4 m. Jika seluruh bagian jalan setapak akan dipasangi ubin dengan ukuran ubin 30 cm × 30 cm, berapa banyak ubin yang diperlukan?
(A) 4.267
(B) 4.367
(C) 4.467
(D) 4.567
Jawaban: A
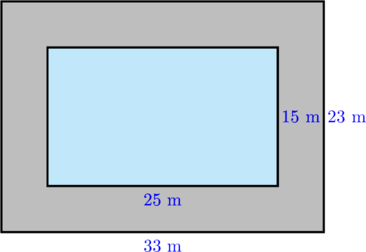
Luas jalan setapak yang dipasangi ubin = (33 × 23) − (25 × 15) m²
Luas jalan setapak yang dipasangi ubin = 759 − 375 m²
Luas jalan setapak yang dipasangi ubin = 384 m²
Luas satu buah ubin = 30 cm × 30 cm = 900 cm² = 0,09 m²
Banyak ubin yang dibutuhkan = luas jalan setapak ÷ luas satu buah ubin
Banyak ubin yang dibutuhkan = 384 m² ÷ 0,09 m²
Banyak ubin yang dibutuhkan = 4.266,67 ≈ 4.267
Soal 03
Sebuah pipa dapat mengisi bak mandi berkapasitas 600 liter dalam waktu 15 menit. Namun, pada saat bersamaan, sebuah lubang kecil di bak tersebut bocor dan mengeluarkan air dengan kecepatan 2,5 liter per menit. Berapa lama waktu yang dibutuhkan hingga bak penuh?
(A) 18 menit
(B) 17 menit
(C) 16 menit
(D) 15 menit
Jawaban: C
Diketahui:
- Pipa mengalirkan air 600 liter dalam 15 menit, berarti debitnya:
600 ÷ 15 = 40 liter/menit - Lubang bocor mengeluarkan air 2,5 liter/menit
- Debit bersih = 40 – 2,5= 37,5 liter/menit
- Ditanya: Waktu yang dibutuhkan untuk mengisi penuh bak?
Penyelesaian:
Waktu = 600 ÷ 37,5
Waktu = 6.000 ÷ 375 = 16 menit
Soal 04
Data jumlah buku yang dipinjam oleh 6 siswa dalam satu bulan di sebuah perpustakaan sekolah adalah sebagai berikut:
10, 12, 14, 10, 18, dan 16.
Jika satu siswa lagi yang bernama Jono meminjam buku sehingga nilai rata-rata pinjaman menjadi 14 buku, berapa jumlah buku yang dipinjam Jono selama satu bulan?
(A) 14 buku
(B) 16 buku
(C) 18 buku
(D) 20 buku
Jawaban: C
Jumlah buku yang dipinjam oleh 6 anak = 10 + 12 + 14 + 10 + 18 + 16 = 80 buku
Misal jumlah buku yang dipinjam Jono = x buah
Jumlah buku yang dipinjam oleh 7 anak = (80 + x) buah
Rata-rata baru = (jumlah buku yang dipinjam oleh 7 anak) ÷ 7
14 = (80 + x) ÷ 7
Kalikan kedua ruas dengan 7
98 = 80 + x
x = 98 − 80
x = 18
Jadi, selama sebulan Jono telah meminjam sebanyak 18 buku dari perpustakaan sekolah.
Soal 05
Sebuah toko elektronik memberikan diskon 20% untuk semua barang. Seorang pelanggan membeli sebuah TV yang harga awalnya (sebelum diskon) Rp4.500.000. Setelah mendapatkan diskon, pelanggan tersebut masih harus membayar pajak sebesar 10% dari harga setelah diskon.
Berapa jumlah uang yang harus dibayarkan pelanggan setelah diskon dan pajak?
(A) Rp3.960.000
(B) Rp3.990.000
(C) Rp4.050.000
(D) Rp4.080.000
Jawaban: A
Hitung harga setelah diskon
Diskon = 20% × 4.500.000 = 900.000
Harga setelah diskon = 4.500.000 − 900.000 = Rp3.600.000
Hitung pajak 10% dari harga setelah diskon
Pajak = 10% × 3.600.000 = Rp360.000
Hitung total harga yang harus dibayar
Total harga = 3.600.000 + 360.000 = Rp3.960.000
Jadi, jumlah uang yang harus dibayarkan pelanggan setelah diskon dan pajak adalah Rp3.960.000
Soal 06
Pak Budi memiliki beberapa tongkat kayu dengan panjang 75 cm, 90 cm, dan 120 cm. Ia ingin memotong tongkat-tongkat tersebut menjadi beberapa bagian yang sama panjang dan sebesar mungkin tanpa ada sisa.
Berapa panjang maksimal setiap potongan tongkat, dan berapa banyak potongan yang dihasilkan?
(A) Panjang 15 cm, total 19 potongan
(B) Panjang 30 cm, total 9 potongan
(C) Panjang 45 cm, total 6 potongan
(D) Panjang 25 cm, total 12 potongan
Jawaban: A
Langkah 1: cari FPB (Faktor Persekutuan Terbesar) dari 75, 90, dan 120
Faktorisasi prima dari 75 = 3 × 5²
Faktorisasi prima dari 90 = 2 × 3² × 5
Faktorisasi prima dari 120 = 2³ × 3 × 5
Faktor persekutuan terbesar adalah faktor persekutuan prima dengan pangkat terkecil
FPB dari 75, 90, dan 12 adalah 3 × 5 = 15 cm
Langkah 2: hitung jumlah potongan
- 75 cm ÷ 15 cm = 5 potong
- 90 cm ÷ 15 cm = 6 potong
- 120 cm ÷ 15 cm = 8 potong
- Total potongan = 5 + 6 + 8 = 19 potong
Jadi, setiap potongan memiliki panjang 15 cm dan total potongannya ada 19.
