Rumus Cermin
\(\color{blue}\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
Keterangan:
- \(f\) = jarak fokus cermin cekung (bernilai positif)
- \(s_0\) = jarak benda ke cermin
- \(s_i\) = jarak bayangan ke cermin
- Jika \(s_i\) bernilai negatif maka bayangan bersifat maya (terletak di belakang cermin)
Rumus Perbesaran
\(\color{blue} M = \dfrac{-s_i}{s_0}\)
\(\color{blue} M = \dfrac{h_i}{h_0}\)
Keterangan:
- \(h_0\) = tinggi benda
- \(h_i\) = tinggi bayangan
- Jika \(M\) bernilai positif artinya bayangan tegak, sebaliknya jika \(M\) bernilai negatif artinya bayangan terbalik
Latihan Soal
Soal 1
Sebuah benda diletakkan pada jarak 5 cm di depan cermin cekung yang memiliki jarak fokus 10 cm. Tentukan:
a. Letak bayangan
b. Perbesaran
c. Sifat bayangan
a. Menghitung jarak bayangan ke cermin
\(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{10} = \dfrac{1}{5} + \dfrac{1}{s_i}\)
\(\dfrac{1}{s_i} = \dfrac{1}{10} – \dfrac{1}{5}\)
\(\dfrac{1}{s_i} = \dfrac{1}{10} – \dfrac{2}{10}\)
\(\dfrac{1}{s_i} = \dfrac{-1}{10}\)
\(s_i = -10 \text{ cm}\)
Bayangan terletak pada jarak 10 cm di belakang cermin
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-(-10)}{5}\)
\(M = 2\)
Bayangan diperbesar 2 kali dari ukuran semula
c. Sifat-sifat bayangan
- Karena nilai \(s_i\) negatif maka bayangan bersifat maya
- Karena nilai \(M\) positif maka bayangan tegak
- Karena nilai \(|M| > 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat maya, tegak, dan diperbesar
Soal 2
Sebuah benda diletakkan pada jarak 6 cm di depan cermin cekung dan menghasilkan bayangan nyata sejauh 12 cm dari cermin cekung. Tentukan:
a. Jarak fokus cermin cekung
b. Perbesaran
c. Sifat bayangan
a. Menghitung jarak fokus cermin cekung
\(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{f} = \dfrac{1}{6} + \dfrac{1}{12}\)
\(\dfrac{1}{f} = \dfrac{2}{12} + \dfrac{1}{12}\)
\(\dfrac{1}{f} = \dfrac{3}{12}\)
\(f = \dfrac{12}{3} = 4 \text{ cm}\)
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-12}{6}\)
\(M = -2\)
\(|M| = 2\)
Bayangan diperbesar 2 kali dari ukuran semula
c. Sifat-sifat bayangan
- Nyata
- Karena nilai \(M\) negatif maka bayangan terbalik
- Karena nilai \(|M| > 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat nyata, terbalik, dan diperbesar
Soal 3
Sebuah benda diletakkan di depan sebuah cermin cekung yang memiliki jari-jari kelengkungan sebesar 12 cm. Bayangan terbentuk di belakang cermin pada jarak 4 cm dari cermin. Tentukan:
a. Letak benda
b. Perbesaran
c. Sifat bayangan
Jarak fokus sama dengan setengah jari-jari kelengkungan cermin. \(f = 6 \text{ cm}\)
Karena bayangan terbentuk di belakang cermin maka \(s_i\) bernilai negatif. \(s_i = -4 \text{ cm}\)
a. Menghitung jarak benda dari cermin
\(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{6} = \dfrac{1}{s_0} + \dfrac{1}{-4}\)
\(\dfrac{1}{s_0} = \dfrac{1}{6} + \dfrac{1}{4}\)
\(\dfrac{1}{s_0} = \dfrac{2}{12} + \dfrac{3}{12}\)
\(\dfrac{1}{s_0} = \dfrac{5}{12}\)
\(s_0 = \dfrac{12}{5} = 2\dfrac{2}{5} \text{ cm}\)
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-(-4)}{\frac{12}{5}}\)
\(M = 4\times \dfrac{5}{12}\)
\(M = \dfrac{5}{3} = 1\dfrac{2}{3}\)
Bayangan diperbesar \(1\dfrac{2}{3}\) kali dari ukuran semula
c. Sifat-sifat bayangan
- Karena bayangan terbentuk di belakang cermin, maka bayangan bersifat maya
- Karena nilai \(M\) positif maka bayangan tegak
- Karena nilai \(|M| > 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat maya, tegak, dan diperbesar
Soal 4
Sebuah bayangan nyata dengan nilai perbesaran \(\frac{2}{3}\) kali, terbentuk pada jarak 10 cm dari cermin cekung. Tentukan:
a. Letak benda
b. Jarak fokus cermin cekung
c. Sifat bayangan
a. Menghitung jarak benda dari cermin dari nilai perbesaran yang diketahui
Karena bayangan bersifat nyata maka bayangan dalam posisi terbalik, sehingga \(M\) ditulis negatif
Jarak bayangan \(s_i\) ditulis positif karena terletak di depan cermin
\(M = \dfrac{-s_i}{s_0}\)
\(-\dfrac{2}{3} = \dfrac{-10}{s_0}\)
kalikan kedua ruas dengan -1
\(\dfrac{2}{3} = \dfrac{10}{s_0}\)
Kali silang
\(2\cdot s_0 = 3 \times 10\)
\(2\cdot s_0 = 30\)
\(s_0 = \dfrac{30}{2} = 15 \text{ cm}\)
Jadi benda berada pada jarak 15 cm di depan cermin cekung
b. Menghitung jarak fokus cermin
\(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{f} = \dfrac{1}{15} + \dfrac{1}{10}\)
\(\dfrac{1}{f} = \dfrac{2}{30} + \dfrac{3}{30}\)
\(\dfrac{1}{f} = \dfrac{5}{30}\)
\(\dfrac{1}{f} = \dfrac{1}{6}\)
\(f = 6 \text{ cm}\)
c. Sifat-sifat bayangan
- Nyata
- Terbalik
- Karena nilai \(|M|< 1\) maka bayangan diperkecil
Sehingga dapat disimpulkan bahwa bayangan bersifat nyata, terbalik, dan diperkecil
Soal 5
Sebuah benda diletakkan di depan cermin cekung dengan jari-jari kelengkungan sebesar 8 cm. Bayangan nyata terbentuk dengan nilai perbesaran 2 kali. Tentukan:
a. Letak benda dan letak bayangan
b. Perbesaran
c. Sifat bayangan
a. Mencari jarak benda dari cermin
Gunakan rumus perbesaran terlebih dahulu
Karena bayangan bersifat nyata maka bayangan dalam posisi terbalik, sehingga \(M\) ditulis negatif
\(M = \dfrac{-s_i}{s_0}\)
\(-2 = \dfrac{-s_i}{s_0}\)
Kalikan kedua ruas dengan -1
\(2 = \dfrac{s_i}{s_0}\)
\(s_i = 2s_0\)
Selanjutnya substitusikan \(s_i = 2s_0\) ke dalam rumus \(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{4} = \dfrac{1}{s_0} + \dfrac{1}{2s_0}\)
\(\dfrac{1}{4} = \dfrac{2}{2s_0} + \dfrac{1}{2s_0}\)
\(\dfrac{1}{4} = \dfrac{3}{2s_0}\)
Kali silang
\(2s_0 = 4\times 3\)
\(s_0 = \dfrac{12}{2} = 6 \text{ cm}\)
Jadi benda terletak pada jarak 6 cm di depan cermin cekung
Mencari jarak bayangan dari cermin
\(s_i = 2\cdot s_0\)
\(s_i = 2\times 6 = 12 \text{ cm}\)
Jadi bayangan terletak pada jarak 12 cm di depan cermin cekung
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-12}{6}\)
\(M = -2\)
\(|M| = 2\)
Bayangan diperbesar 2 kali semula
c. Sifat-sifat bayangan
- Karena bayangan terletak di depan cermin, maka bayangan bersifat nyata
- Karena nilai \(M\) negatif maka posisi bayangan terbalik
- Karena nilai \(|M|> 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat nyata, terbalik, dan diperbesar
Soal 6
Sebuah benda diletakkan di depan cermin cekung yang memiliki jarak fokus 8 cm. Bayangan maya yang terjadi berjarak 12 cm dari benda. Tentukan:
a. Letak benda dan letak bayangan
b. Perbesaran
c. Sifat bayangan
a. Mencari jarak benda dan jarak bayangan ke cermin
Diketahui jarak antara benda dengan bayangan adalah 12 cm
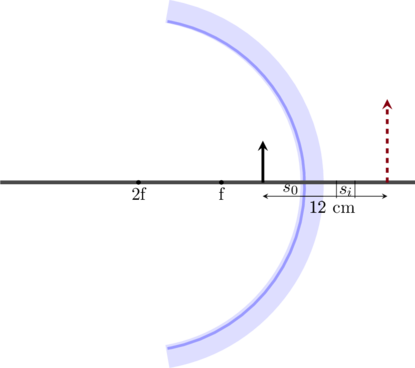
\(s_0 + |s_i| = 12 \text{ cm}\)
\(|s_i| = 12 – s_0\)
Karena bayangan bersifat maya maka \(s_i\) ditulis negatif
\(s_i= -(12 – s_0)\)
\(s_i= s_0 – 12\)
Selanjutnya substitusikan \(s_i= s_0 – 12\) ke dalam rumus \(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{8} = \dfrac{1}{s_0} + \dfrac{1}{s_0 – 12}\)
\(\dfrac{1}{8} = \dfrac{s_0 – 12 }{s_0(s_0 – 12)} +\dfrac{s_0 }{s_0(s_0 – 12)} \)
\(\dfrac{1}{8} = \dfrac{2s_0 – 12 }{s_0(s_0 – 12)}\:\:\:\:\:\:\color{blue} \text{ kalikan silang}\)
\(s_0(s_0 – 12) = 8(2s_0 – 12)\)
\(s_0^2 – 12s_0 = 16s_0 – 96\)
\(s_0^2 – 28s_0 + 96 = 0\)
\((s_0 – 24)(s_0 – 4) = 0\)
\(s_0 = 24 \text{ cm}\:\:\:\:\:\color{red} \text{TM}\)
\(s_0 = 4\text{ cm}\)
Benda terletak pada jarak 4 cm di depan cermin cekung
Selanjutnya menghitung jarak bayangan yang terjadi
\(s_i= s_0 – 12\)
\(s_i= 4 – 12\)
\(s_i= -8 \text{ cm}\)
Bayangan terletak 8 cm di belakang cermin cekung
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-(-8)}{4}\)
\(M = 2\)
Bayangan diperbesar 2 kali semula
c. Sifat-sifat bayangan
- Karena bayangan terletak di belakang cermin, maka bayangan bersifat maya
- Karena nilai \(M\) positif maka posisi bayangan tegak
- Karena nilai \(|M|> 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat maya, tegak, dan diperbesar
Soal 7
Sebuah benda diletakkan diantara titik fokus dan jari-jari kelengkungan cermin cekung. Diketahui jarak titik fokus cermin tersebut 5 cm. Jika bayangan nyata yang terjadi berjarak 24 cm dari benda maka tentukan:
a. Letak benda dan letak bayangan
b. Perbesaran
c. Sifat bayangan
Diketahui jarak antara benda dengan bayangan adalah 24 cm
Posisi benda di ruang II (antara \(f\) dan \(2f\)) maka bayangan yang terbentuk berada di ruang III (> \(2f\))
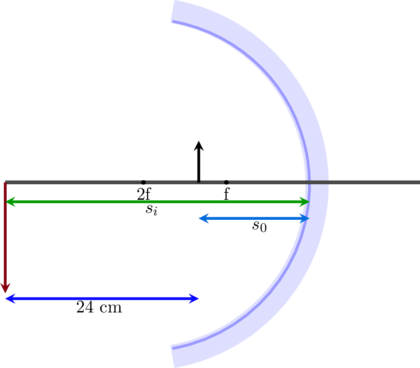
Dari gambar di atas,
\(s_i – s_0 = 24 \text{ cm}\)
\(s_i = 24 + s_0\text{ cm}\)
Selanjutnya substitusikan \(s_i= 24 + s_0 \) ke dalam rumus \(\dfrac{1}{f} = \dfrac{1}{s_0} + \dfrac{1}{s_i}\)
\(\dfrac{1}{5} = \dfrac{1}{s_0} + \dfrac{1}{24 + s_0}\)
\(\dfrac{1}{5} = \dfrac{24 + s_0}{s_0(24 + s_0)} + \dfrac{s_0}{24 + s_0}\)
\(\dfrac{1}{5} = \dfrac{24 + 2s_0}{s_0(24 + s_0)}\:\:\:\:\:\:\color{blue} \text{ kalikan silang}\)
\(s_0(24 + s_0) = 5(24 + 2s_0)\)
\(24s_0 + s_0^2) = 120 + 10s_0)\)
\(s_0^2 + 14s_0 – 120 = 0\)
\((s_0 + 20)(s_0 – 6) = 0\)
\(s_0 = -20 \text{ cm}\:\:\:\:\:\color{red} \text{TM}\)
\(s_0 = 6 \text{ cm}\)
Benda terletak 6 cm di depan cermin cekung
Selanjutnya menghitung jarak bayangan yang terjadi
\(s_i= 24 + s_0\)
\(s_i= 24 + 6\)
\(s_i= 30 \text{ cm}\)
Bayangan terletak 30 cm di depan cermin cekung
b. Menghitung nilai perbesaran
\(M = \dfrac{-s_i}{s_0}\)
\(M = \dfrac{-30}{6}\)
\(M = -5\)
\(|M| = 5\)
Bayangan diperbesar 5 kali semula
c. Sifat-sifat bayangan
- Karena bayangan terletak di depan cermin, maka bayangan bersifat nyata
- Karena nilai \(M\) negatif maka posisi bayangan terbalik
- Karena nilai \(|M|> 1\) maka bayangan diperbesar
Sehingga dapat disimpulkan bahwa bayangan bersifat nyata, terbalik, dan diperbesar
