A. Benda berada pada bidang miring yang licin
Pada bidang miring dibuat sumbu koordinat x searah dengan bidang miringnya.
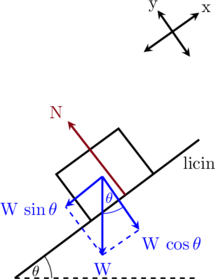
Resultan gaya arah sumbu x
\(\sum\textbf{F}_x = \textbf{m}\cdot \textbf{a}\)
\(\textbf{W}\cdot \sin \theta = \textbf{m}\cdot \textbf{a}\)
Resultan gaya arah sumbu y
\(\sum\textbf{F}_y = 0\)
\(\textbf{N}\:-\:\textbf{W}\cdot \cos \theta = 0\)
\(\textbf{N} = \textbf{W}\cdot \cos \theta\)
B. Benda berada pada bidang miring yang kasar
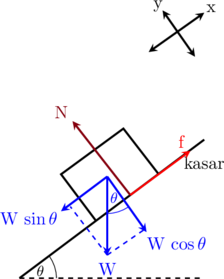
Resultan gaya arah sumbu y
\(\sum\textbf{F}_y = 0\)
\(\textbf{N}\:-\:\textbf{W}\cdot \cos \theta = 0\)
\(\textbf{N} = \textbf{W}\cdot \cos \theta\)
Resultan gaya arah sumbu x
Benda diam
Benda akan bergerak menuruni bidang miring jika \(\textbf{W}\cdot \sin \theta < \textbf{f}_{s\:max}\)
Cara menghitung gaya gesekan statis maksimum:
\(\textbf{f}_{s\:max} = \mu_s \cdot \textbf{N}\)
Benda bergerak
Benda akan bergerak menuruni bidang miring jika \(\textbf{W}\cdot \sin \theta > \textbf{f}_{s\:max}\)
\(\sum\textbf{F}_x = \textbf{m}\cdot \textbf{a}\)
\(\textbf{W}\cdot \sin \theta\:-\:\textbf{f}_{k} = \textbf{m}\cdot \textbf{a}\)
Cara menghitung gaya gesekan kinetis:
\(\textbf{f}_{k} = \mu_k \cdot \textbf{N}\)
C. Benda berada pada bidang miring yang kasar dan diberi gaya mendatar F
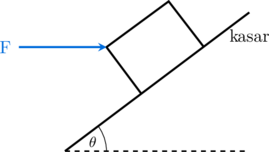
Jika benda bergerak, maka arah geraknya ada 2 kemungkinan
Kemungkinan 1: Benda bergerak ke bawah
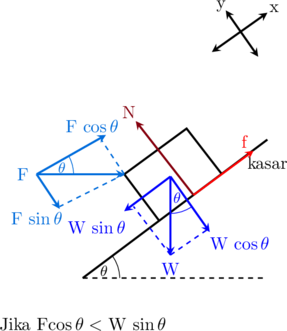
Resultan gaya arah sumbu y
\(\sum\textbf{F}_y = 0\)
\(\textbf{N}\:-\:\textbf{W}\cdot \cos \theta\:-\: \textbf{F}\cdot \sin \theta= 0\)
\(\textbf{N} = \textbf{W}\cdot \cos \theta + \textbf{F}\cdot \sin \theta\)
Resultan gaya arah sumbu x
\(\sum\textbf{F}_x = \textbf{m}\cdot \textbf{a}\)
\(\textbf{W}\cdot \sin \theta\:-\:\textbf{f}_{k}\:-\: \textbf{F}\cdot \cos \theta= \textbf{m}\cdot \textbf{a}\)
Kemungkinan 2: Benda bergerak ke atas
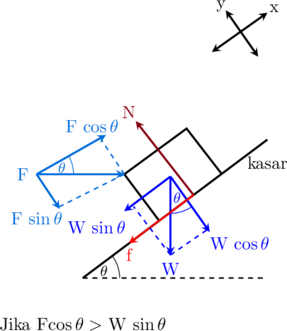
Resultan gaya arah sumbu y
\(\sum\textbf{F}_y = 0\)
\(\textbf{N}\:-\:\textbf{W}\cdot \cos \theta\:-\: \textbf{F}\cdot \sin \theta= 0\)
\(\textbf{N} = \textbf{W}\cdot \cos \theta + \textbf{F}\cdot \sin \theta\)
Resultan gaya arah sumbu x
\(\sum\textbf{F}_x = \textbf{m}\cdot \textbf{a}\)
\(\textbf{F}\cdot \cos \theta\:-\:\textbf{f}_{k}\:-\: \textbf{W}\cdot \sin \theta= \textbf{m}\cdot \textbf{a}\)
