Soal 1
Sebuah kotak bermassa 20 kg diam di atas lantai yang kasar dengan koefisien gesekan 0,3 dan 0,2. Kotak tersebut kemudian ditekan dengan gaya F sebesar 40 N, membentuk sudut 37° terhadap horizontal seperti pada gambar di bawah ini:

A. Selidiki apakah benda bergerak, tepat akan bergerak, atau tidak bergerak?
B. Tentukan besar gaya gesekan antara benda dengan lantai.
C. Tentukan percepatan benda tersebut.
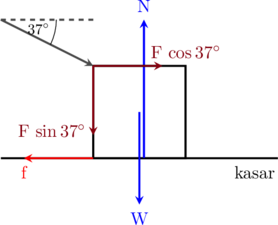
A. Menentukan apakah benda bergerak, tepat akan bergerak, atau tidak bergerak
Menghitung gaya normal
\(\sum \text{F}_y = 0\)
\(\text{N} \:-\: \text{W}\:-\:\text{F}\sin 37^{\circ} = 0\)
\(\text{N}\:-\: \text{m}\cdot \text{g} \:-\: \text{F}\sin 37^{\circ} = 0\)
\(\text{N}\:-\: 20\cdot 10\:-\: 40\cdot 0,6 = 0\)
\(\text{N}\:-\: 200\:-\: 24 = 0\)
\(\text{N} = 224 \text{ Newton}\)
Bandingkan nilai antara \(\text{F}\cos 37^{\circ}\) dengan nilai \(f_{\text{s max}}\)
\(\text{F}\cos 37^{\circ}\dotso f_{\text{s max}}\)
\(20\text{ N}\cdot 0,8 \dotso \mu_{\text{s}}\cdot \text{N}\)
\(16\text{ N} \dotso 0,3\cdot 224\text{ N}\)
\(16\text{ N} < 67,2\text{ N}\)
Karena \(\text{F}\cos 37^{\circ} < f_{\text{s max}}\) maka benda tidak bergerak
B. Menentukan besar gaya gesek
Karena benda tidak bergerak, maka besar gaya gesek statis antara benda dengan lantai sama dengan gaya tarik mendatarnya yaitu \(\text{F}\cos 37^{\circ}\)
\(f_{\text{s}} = \text{F}\cos 37^{\circ}\)
\(f_{\text{s}} = 40\cdot 0,8 = 32 \text{ N}\)
C. Menentukan percepatan benda
Karena benda tidak bergerak, maka nilai percepatan benda sama dengan nol
Soal 2
Tiga buah benda masing-masing bermassa \(\text{m}_1 = 3 \text{ kg}, \text{m}_2 = 4 \text{ kg}\), dan \(\text{m}_3 = 5 \text{ kg}\) dihubung dengan tali di atas lantai yang licin, kemudian ditarik dengan gaya \(\text{F} = 120 \text{ N}\).
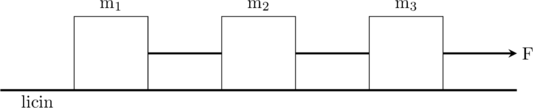
Tentukan:
A. Percepatan sistem
B. Tegangan tali antara benda 1 dengan benda 2
C. Tegangan tali antara benda 2 dan benda 3
Gambar diagram gaya:
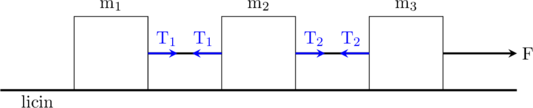
Gerak benda ke arah kanan, gaya yang searah dengan gerak benda ditulis positif
Tinjau benda 1
\(\sum \text{F}_x = \text{m}_{1}\cdot \text{a}\)
\(\text{T}_1 = \text{m}_{1}\cdot \text{a}\)
\(\text{T}_1 = 3\text{a}\)
Tinjau benda 2
\(\sum \text{F}_x = \text{m}_{2}\cdot \text{a}\)
\(\text{T}_2\:-\:\text{T}_1 = \text{m}_{2}\cdot \text{a}\)
\(\text{T}_2\:-\:3\text{a} = 4\text{a}\)
\(\text{T}_2= 4\text{a} + 3\text{a} = 7\text{a}\)
Tinjau benda 3
\(\sum \text{F}_x = \text{m}_{3}\cdot \text{a}\)
\(\text{F}\:-\:\text{T}_2 = \text{m}_{3}\cdot \text{a}\)
\(120\:-\:7\text{a} = 5\text{a}\)
\(120 = 5\text{a} + 7\text{a}\)
\(120 = 12\text{a}\)
\(\text{a} = 120 \div 12 = 10 \text{ m/s²}\)
Percepatan sistem adalah 10 m/s²
Substitusikan nilai percepatan ini ke persamaan \(\text{T}_1 = 3\text{a}\) dan \(\text{T}_2 = 7\text{a}\), sehingga diperoleh tegangan tali \(\text{T}_1 = 30 \text{ N}\) dan \(\text{T}_2 = 70 \text{ N}\).
Jadi besar tegangan tali antara benda 1 dengan benda 2 adalah 30 N dan besar tegangan tali antara benda 2 dengan benda 3 adalah 70 N.
Soal 3
Tiga buah benda masing-masing bermassa \(\text{m}_1 = 2 \text{ kg}, \text{m}_2 = 3 \text{ kg}\), dan \(\text{m}_3 = 4 \text{ kg}\) saling berhimpit di atas lantai yang kasar dan kemudian didorong dengan gaya F sebesar 54 N, seperti pada gambar di bawah ini:
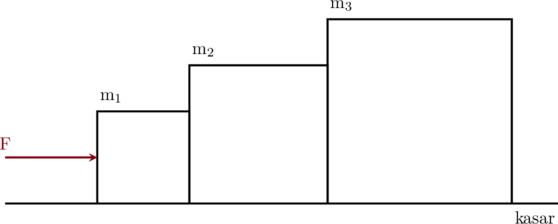
Jika koefisien gesekan kinetis antara benda dengan lantai sebesar 0,2, maka tentukan:
A. Percepatan sistem
B. Besar gaya kontak yang terjadi antara benda 1 dengan benda 2
C. Besar gaya kontak yang terjadi antara benda 2 dengan benda 3
Gambar diagram gaya:
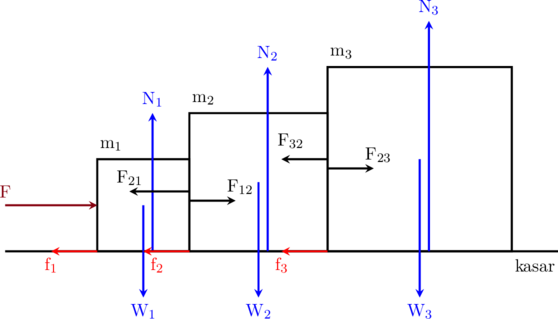
A. Menghitung Percepatan Sistem
\(\sum \text{F}_x = \text{m}_{\text{total}}\cdot \text{a}\)
\(\text{F}\:-\:\text{f}_1 \:-\:\text{F}_{21} + \text{F}_{12}\:-\:\text{f}_2\:-\: \text{F}_{32} + \text{F}_{23}\:-\:\text{f}_3 = (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(\text{F}\:-\:\text{f}_1 \:-\:\cancel{\text{F}_{21}} + \cancel{\text{F}_{12}}\:-\:\text{f}_2\:-\: \cancel{\text{F}_{32}} + \cancel{\text{F}_{23}}\:-\:\text{f}_3 = (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(\text{F}\:-\:\mu_k \cdot \text{N}_1\:-\:\mu_k \cdot \text{N}_2\:-\:\mu_k \cdot \text{N}_3= (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(\text{F}\:-\:\mu_k \cdot \text{W}_1\:-\:\mu_k \cdot \text{W}_2\:-\:\mu_k \cdot \text{W}_3= (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(\text{F}\:-\:\mu_k \cdot \text{m}_1\cdot \text{g}\:-\:\mu_k \cdot \text{m}_2\cdot \text{g}\:-\:\mu_k\cdot \text{m}_3\cdot \text{g}= (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(54\:-\:0,2\cdot 2\cdot 10\:-\:0,2\cdot 3\cdot 10\:-\:0,2 \cdot 4\cdot 10 = (2 + 3 + 4)\cdot \text{a}\)
\(54\:-\:4\:-\:6\:-\:8 = (2 + 3 + 4)\cdot \text{a}\)
\(54\:-\:4\:-\:6\:-\:8 = (2 + 3 + 4)\cdot \text{a}\)
\(36 = 9\text{a}\)
\(a = 4 \text{ m/s²}\)
B. Menghitung \(\text{F}_{12}\)
Tinjau benda 1
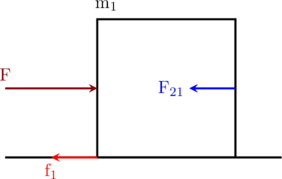
\(\sum \text{F}_x = \text{m}_{1}\cdot \text{a}\)
\(\text{F}\:-\:\text{f}_1\:-\:\text{F}_{21} = \text{m}_{1}\cdot \text{a}\)
\(54\:-\:4\:-\:\text{F}_{21} = 2\cdot 4\)
\(50\:-\:\text{F}_{21} = 8\)
\(\text{F}_{21} = 42\text{ Newton}\)
Jadi besar gaya kontak antara benda 1 dengan benda 2 adalah 42 N
C. Menghitung \(\text{F}_{23}\)
Tinjau benda 3
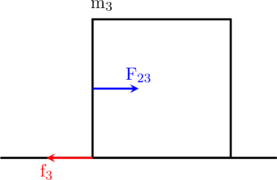
\(\sum \text{F}_x = \text{m}_{3}\cdot \text{a}\)
\(\text{F}_{23} \:-\:\text{f}_3 = \text{m}_{3}\cdot \text{a}\)
\(\text{F}_{23} \:-\:8 = 4\cdot 4\)
\(\text{F}_{23} = 16 + 8\)
\(\text{F}_{23} = 24\text{ Newton}\)
Jadi besar gaya kontak antara benda 2 dengan benda 3 adalah 24 N
Soal 4
Perhatikan gambar di bawah ini:
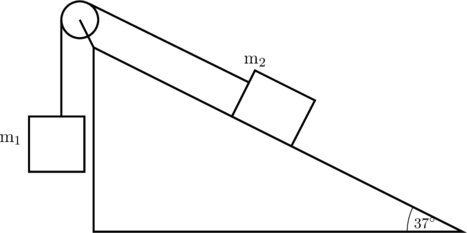
Benda 1 bermassa 10 kg dihubung tali melewati sebuah katrol licin dengan benda 2 yang bermassa 12 kg. Benda 2 berada pada bidang miring kasar dengan koefisien gesekan 0,25 dan 0,1.
A. Tentukan apakah benda 1 dan benda 2 bergerak, tepat akan bergerak, atau tidak bergerak? Jika bergerak kemana arahnya?
B. Tentukan nilai percepatan sistem
C. Tentukan besar tegangan tali
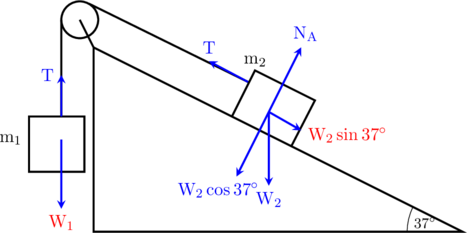
\(\color{red} \text{W}_1 = \text{m}_1\cdot \text{g}\)
\(\color{red} \text{W}_1 = 10\cdot 10\)
\(\color{red} \text{W}_1 = 100 \text{ N}\)
\(\color{red} \text{W}_2\sin 37^{\circ} = \text{m}_2\cdot \text{g}\cdot \sin 37^{\circ}\)
\(\color{red} \text{W}_2\sin 37^{\circ} = 12\cdot 10\cdot 0,6\)
\(\color{red} \text{W}_2\sin 37^{\circ} = 72 \text{ N}\)
Menghitung \(\text{N}_{\text{A}}\)
\(\sum \text{F}_y = 0\)
\(\text{N}_{\text{A}}\:-\:\text{W}_2\cos 37^{\circ} = 0\)
\(\text{N}_{\text{A}}\:-\:120\cdot 0,8 = 0\)
\(\text{N}_{\text{A}}\:-\:96= 0\)
\(\text{N}_{\text{A}}= 96 \text{ N}\)
A. Menentukan apakah benda 1 dan benda 2 bergerak, tepat akan bergerak atau tidak bergerak
Bandingkan nilai \(\color{red} \text{W}_1\:-\:\text{W}_2\sin 37^{\circ}\) dengan \(\color{red}\text{f}_{\text{ s max}}\)
\(\color{red} \text{W}_1\:-\:\text{W}_2\sin 37^{\circ}\dotso \text{f}_{\text{ s max}}\)
\(\color{red} 100\:-\:72 \text{ N}\dotso \mu_s \cdot \text{N}_{\text{A}}\)
\(\color{red} 28 \text{ N}\dotso 0,25 \cdot 96 \text{ N}\)
\(\color{red} 28 \text{ N} > 24 \text{ N}\)
Karena \(\text{W}_1\:-\:\text{W}_2\sin 37^{\circ} >\text{f}_{\text{ s max}}\), maka benda bergerak.
Arah gerak benda:
- Benda 1 turun ke bawah
- Benda 2 tertarik ke atas bidang miring
B. Menentukan nilai percepatan sistem
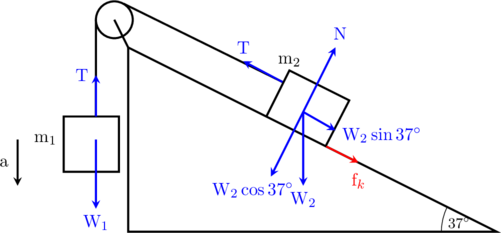
Tinjau sistem,
\(\sum \text{F} = \text{m}_t \cdot \text{a}\)
\(\text{W}_1\:-\:\cancel{\text{T}} + \cancel{\text{T}}\:-\:\text{W}_2\sin 37^{\circ}\:-\:\text{f}_k = (\text{m}_1 + \text{m}_2) \cdot \text{a}\)
\(100\:-\:72\:-\:\mu_k\cdot \text{N}_{\text{A}} = (10 + 12) \cdot \text{a}\)
\(28\:-\:0,1\cdot 96 = 22\text{a}\)
\(28\:-\:9,6= 22\text{a}\)
\(18,4 = 22\text{a}\)
\(\text{a} = \dfrac{18,4}{22}\)
\(\text{a} = \dfrac{46}{55} = 0,84 \text{ m/s²}\)
Jadi kedua benda bergerak dengan nilai percepatan \(0,84 \text{ m/s²}\)
C. Menentukan tegangan tali
Tinjau benda 1
\(\sum \text{F} = \text{m}_1\cdot \text{a}\)
\(\text{W}_1 \:-\:\text{T} = \text{m}_1\cdot \text{a}\)
\(100 \:-\:\text{T} = 10\cdot \dfrac{46}{55}\)
\(100\:-\:\text{T} = \dfrac{92}{11}\)
\(\text{T} = \dfrac{1008}{11} = 91,6 \text{ N}\)
Jadi tegangan talinya sebesar \(91,6 \text{ N}\)
Soal 5
Tiga buah benda dihubung tali pada katrol tetap yang licin seperti pada gambar di bawah ini:
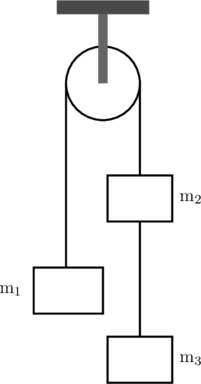
Jika diketahui \(\text{m}_2 = \text{m}_3 = 2 \text{ kg}\) dan \(\text{m}_1 = 3 \text{ kg}\), maka tentukan:
A. Nilai percepatan sistem
B. Tegangan masing-masing tali
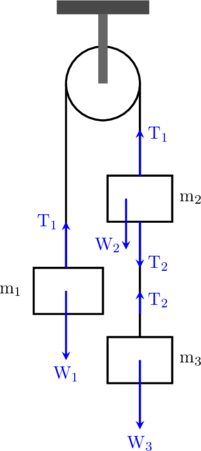
\(\text{W}_1 = \text{m}_1\cdot \text{g}\)
\(\text{W}_1 = 3\cdot 10\)
\(\text{W}_1 = 30 \text{ N}\)
\(\text{W}_2 = \text{m}_2\cdot \text{g}\)
\(\text{W}_2= 2\cdot 10\)
\(\text{W}_2 = 20 \text{ N}\)
\(\text{W}_3= 20 \text{ N}\)
\(\text{W}_2 + \text{W}_3 = 20 + 20 = 40 \text{ N}\)
Karena \(\text{W}_2 + \text{W}_3 > \text{W}_1\), maka arah gerak benda adalah:
- Benda 1 tertarik ke atas
- Benda 2 dan 3 turun ke bawah
A. Menentukan percepatan sistem
Tinjau sistem
\(\sum \text{F}_y = \text{m}_t \cdot \text{a}\)
\(\text{W}_3 \:-\:\text{T}_2 + \text{W}_2 + \text{T}_2 \:-\:\text{T}_1 + \text{T}_1 \:-\:\text{W}_1 = (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(\text{W}_3 \:-\:\cancel{\text{T}_2} + \text{W}_2 + \cancel{\text{T}_2} \:-\:\cancel{\text{T}_1} + \cancel{\text{T}_1} \:-\:\text{W}_1 = (\text{m}_1 + \text{m}_2 + \text{m}_3)\cdot \text{a}\)
\(20 + 20 \:-\:30 = (3 + 2 + 2)\text{a}\)
\(10 = 7\text{a}\)
\(\text{a} = \dfrac{10}{7}\text{ m/s²}\)
Jadi percepatan sistemnya sebesar \(\dfrac{10}{7}\text{ m/s²}\)
B. Menentukan tegangan masing-masing tali
Tinjau benda 1
\(\sum \text{F}_y = \text{m}_1\cdot \text{a}\)
\(\text{T}_1\:-\:\text{W}_1 = \text{m}_1\cdot \text{a}\)
\(\text{T}_1\:-\:30 = 3\cdot \dfrac{10}{7}\)
\(\text{T}_1 = \dfrac{30}{7} + 30\)
\(\text{T}_1 = \dfrac{240}{7}\text{ N}\)
Tinjau benda 3
\(\sum \text{F}_y = \text{m}_3\cdot \text{a}\)
\(\text{W}_3\:-\:\text{T}_2 = \text{m}_3\cdot \text{a}\)
\(20\:-\:\text{T}_2 = 2\cdot \dfrac{10}{7}\)
\(\text{T}_2 = 20\:-\:\dfrac{20}{7}\)
\(\text{T}_2 = \dfrac{120}{7}\text{ N}\)
Soal 6
Sebuah benda bermassa 2 kg ditekan dengan gaya F = 120 N membentuk sudut 53° terhadap arah vertikal pada sebuah tembok yang kasar.
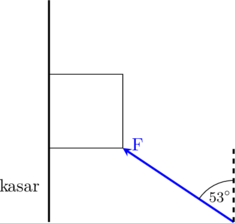
Diketahui juga koefisien gesekan antara benda dengan tembok adalah 0,2 dan 0,4.
Tentukan:
A. Besar gaya normal yang bekerja
B. Selidiki apakah benda bergerak, tepat akan bergerak atau diam
C. Tentukan besar gaya gesek yang bekerja
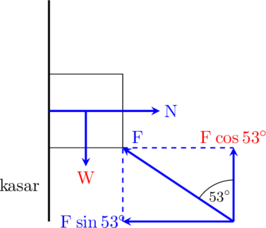
A. Menentukan besar gaya normal
\(\sum \text{F}_x = 0\)
\(\text{N}\:-\:\text{F}\sin 53^{\circ} = 0\)
\(\text{N} = \text{F}\sin 53^{\circ}\)
\(\text{N} = 120 \cdot 0,8 = 96 \text{ N}\)
B. Menentukan apakah benda bergerak, tepat akan bergerak atau diam
Bandingkan besar antara \(\text{F}\cos 53^{\circ}\:-\:\text{W}\) dengan \(\text{f}_{\text {s max}}\)
\(\text{F}\cos 53^{\circ}\:-\:\text{W}\dotso \text{f}_{\text {s max}}\)
\(\text{F}\cos 53^{\circ}\:-\:\text{W}\dotso \mu_{\text{s}}\cdot \text{N}\)
\(120 \cdot (0,6)\:-\:20\dotso 0,4\cdot 96\)
\(52 > 38,2\)
Karena \(\text{F}\cos 53^{\circ}\:-\:\text{W} > \text{f}_{\text {s max}}\) maka benda bergerak ke atas.
C. Menghitung besar gaya gesek
Gaya gesekan yang terjadi adalah gaya gesekan kinetis
\(\text{f}_{\text{k}} = \mu_{\text{k}}\cdot \text{N}\)
\(\text{f}_{\text{k}} = 0,2\cdot 96\)
\(\text{f}_{\text{k}} = 19,2 \text{ N}\)

