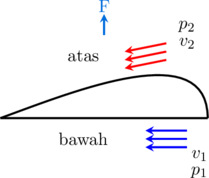
Keterangan:
\(v_1\) = kelajuan udara di bawah sayap pesawat
\(v_2\) = kelajuan udara di atas sayap pesawat
\(p_1\) = tekanan udara di bawah pesawat
\(p_2\) = tekanan udara di atas pesawat
Udara yang mengalir di atas sayap pesawat lebih cepat dibandingkan dengan udara yang mengalir di bawah sayap pesawat
Tekanan udara di atas sayap pesawat lebih kecil dibandingkan tekanan udara di bawah sayap pesawat
Gaya angkat pesawat
\(\color{blue} \text{F} = \dfrac{1}{2} \rho \text{A}(v_2^2\:-\:v_1^2)\)
Keterangan:
ρ = massa jenis udara
A = luas efektif sayap pesawat
Penurunan rumusnya:
\(\text{P}_1 + \rho g h_1 + \dfrac{1}{2} \rho v_1^2 = \text{P}_2 + \rho g h_2 + \dfrac{1}{2} \rho v_2^2\)
anggap \(h_1 = h_2\)
\(\text{P}_1\:-\:\text{P}_2 + \cancel{\rho g h_1} + \dfrac{1}{2} \rho v_1^2 = \cancel{\rho g h_2} + \dfrac{1}{2} \rho v_2^2\)
\(\text{P}_1\:-\:\text{P}_2 + \dfrac{1}{2} \rho v_1^2 = \dfrac{1}{2} \rho v_2^2\)
\(\triangle \text{P} = \dfrac{1}{2} \rho (v_2^2\:-\:v_1^2)\)
\(\dfrac{\text{F}}{\text{A}} = \dfrac{1}{2} \rho (v_2^2\:-\:v_1^2)\)
\(\text{F} = \dfrac{1}{2} \rho \text{A} (v_2^2\:-\:v_1^2)\)
CONTOH SOAL
Soal 1
Udara mengalir horizontal melalui sayap pesawat sehingga kecepatan udara di bagian bawah pesawat 40 m/s dan bagian atas pesawat 50 m/s. Pesawat memiliki massa total 500 kg dan luas efektif sayap pesawat 80 m². Jika massa jenis udara 1,3 kg/m³ dan percepatan gravitasi 10 m/s², maka resultan gaya pada pesawat adalah…
(A) 5000 N
(B) 42000 N
(C) 41800 N
(D) 46800 N
(E) 54200 N