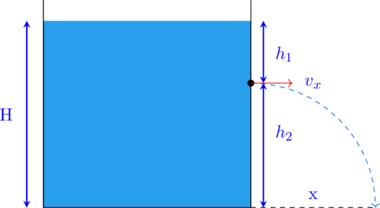
Keterangan:
\(h_1\) = kedalaman titik bocor diukur dari permukaan air
\(h_2\) = ketinggian titik bocor dari dasar (acuan permukaan tanah)
Kelajuan air pada titik kebocoran \(\color{blue} v_x = \sqrt{2 \cdot g \cdot h_1}\)
Jangkauan air maksimum \(\color{blue} x = 2 \sqrt{h_1 \cdot h_2}\) (rumus ini hanya berlaku untuk penampung air yang diletakkan di permukaan tanah)
Jika penampung air berada pada ketinggian tertentu dari permukaan tanah, gunakan rumus gerak parabola:
\(\color{blue} y = y_0 + v_{0y}\cdot t \:-\: \dfrac{1}{2} \cdot g \cdot t^2\)
\(\color{blue} v_{y} = v_{0y}\:-\:g \cdot t\)
\(\color{blue} x = v_{x} \cdot t\)
CONTOH SOAL
Soal 01
Sebuah bak penampung air hanya terisi air 3/4 bagian seperti pada gambar di bawah ini.
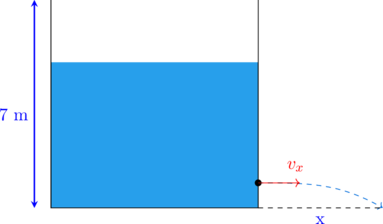
Tepat 0,25 meter di atas dasar bak penampung air terdapat lubang kebocoran.
Tentukan:
A. Kelajuan air yang keluar lewat lubang \((v_x)\)
B. Jarak pancaran maksimum air \((x)\)
A. Menghitung kelajuan air yang keluar lewat lubang
Ketinggian air di dalam bak penampungan \(\dfrac{3}{4} \times 7 = 5,25 \text{ m}\)
Karena terdapat kebocoran 0,25 meter di atas dasar bak, maka kedalaman titik kebocoran tersebut adalah 5,25 − 0,25 = 5 meter
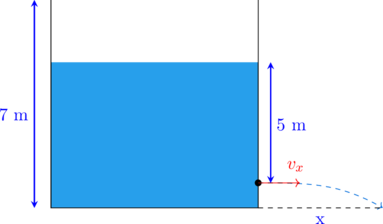
Kelajuan air pada titik kebocoran \(v_x = \sqrt{2 \cdot g \cdot h_1}\)
\(v_x = \sqrt{2 \cdot 10 \cdot 5}\)
\(v_x = \sqrt{100} = 10 \text{ m}\)
B. Menghitung jarak pancaran maksimum air
Jarak pancaran maksimum \(x = 2 \sqrt{h_1 \cdot h_2}\)
Jarak pancaran maksimum \(x = 2 \sqrt{5 \cdot 0,25}\)
Jarak pancaran maksimum \(x = 2 \cdot \dfrac{1}{2}\sqrt{5}\)
Jarak pancaran maksimum \(x = \sqrt{5} \text{ m}\)
Soal 02
Sebuah bak penampung air terisi penuh air seperti pada gambar di bawah ini.
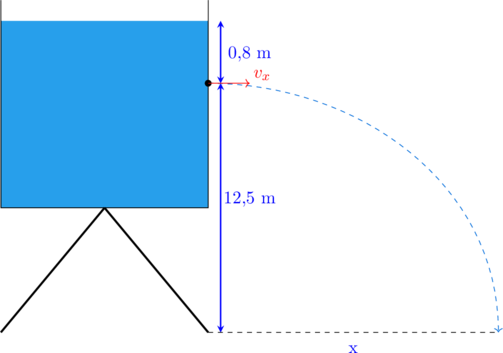
Tepat 12,5 meter dari atas tanah terdapat lubang kebocoran.
Tentukan:
A. Kelajuan air yang keluar lewat lubang \((v_x)\)
B. Jarak pancaran maksimum air \((x)\)
A. Menghitung kelajuan air yang keluar lewat lubang
Kelajuan air pada titik kebocoran \(v_x = \sqrt{2 \cdot g \cdot h_1}\)
\(v_x = \sqrt{2 \cdot 10 \cdot 0,8}\)
\(v_x = \sqrt{16}\)
\(v_x = 4 \text{ m}\)
B. Menghitung jarak pancaran maksimum air
Menghitung waktu yang dibutuhkan air untuk mencapai permukaan tanah
\(y = y_0 + v_{0y} \cdot t \:-\:\dfrac{1}{2} \cdot g \cdot t^2\)
\(0 = 12,5 + 0 \:-\:\dfrac{1}{2} \cdot 10 \cdot t^2\)
\(5t^2 = 12,5\)
\(t^2 = \dfrac{5}{2}\)
\(t = \sqrt{\dfrac{5}{2}}\)
\(t = \sqrt{\dfrac{10}{4}} = \dfrac{1}{2} \sqrt{5} \text{ s}\)
Menghitung jarak pancaran maksimum air
\(x = v_{x} \cdot t\)
\(x = 4 \cdot \dfrac{1}{2} \sqrt{5}\)
\(x = 2\sqrt{5} \text{ m}\)
