Quiz-summary
0 of 14 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 60 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 14 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 14
1. Pertanyaan
1 pointsSebuah patung emas yang massanya 9,65 kg dan massa jenisnya \(5,15 \times 10^3 \text{ kg. m}^{-3}\) berada di dalam kapal yang karam di dasar laut. Patung tersebut akan diangkat ke permukaan laut dengan menggunakan tali kawat baja yang dihubungkan dengan alat penarik. Massa jenis air laut \(1,03 \times 10^3 \text{ kg.m}^{-3}\), maka gaya minimal yang diperlukan untuk mengangkat patung emas tersebut ke permukaan adalah…
Benar
Langkah 1: Menghitung volume patung
\(\rho = \dfrac{m}{V}\)
\(5.150 = \dfrac{9,65}{V}\)
\(V = \dfrac{9,65}{5.150}\)
\(V = 1,87 \times 10^{-3} \text{ m}^{-3}\)
Langkah 2: Menghitung tegangan tali T
\(\sum \text{F}_y = 0\)
\(\text{T} + \text{F}_{\text{A}} \:-\: W = 0\)
\(\text{T} + \text{F}_{\text{A}} = W\)
\(\text{T} + \rho \cdot g \cdot V_t = m \cdot g\)
\(\text{T} + \rho_{\text{air laut}} \cdot g \cdot V_t = m \cdot g\)
\(\text{T} + 1.030\cdot 10 \cdot 1,87 \times 10^{-3} = 9,65 \cdot 10\)
\(\text{T} + 19,261 = 96,5\)
\(\text{T} = 96,5 \:-\: 19,261\)
\(\text{T} = 77,239 \text{ N}\)
\(\text{T} = 77,20 \text{ N}\)
Salah
Langkah 1: Menghitung volume patung
\(\rho = \dfrac{m}{V}\)
\(5.150 = \dfrac{9,65}{V}\)
\(V = \dfrac{9,65}{5.150}\)
\(V = 1,87 \times 10^{-3} \text{ m}^{-3}\)
Langkah 2: Menghitung tegangan tali T
\(\sum \text{F}_y = 0\)
\(\text{T} + \text{F}_{\text{A}} \:-\: W = 0\)
\(\text{T} + \text{F}_{\text{A}} = W\)
\(\text{T} + \rho \cdot g \cdot V_t = m \cdot g\)
\(\text{T} + \rho_{\text{air laut}} \cdot g \cdot V_t = m \cdot g\)
\(\text{T} + 1.030\cdot 10 \cdot 1,87 \times 10^{-3} = 9,65 \cdot 10\)
\(\text{T} + 19,261 = 96,5\)
\(\text{T} = 96,5 \:-\: 19,261\)
\(\text{T} = 77,239 \text{ N}\)
\(\text{T} = 77,20 \text{ N}\)
-
Pertanyaan 2 dari 14
2. Pertanyaan
1 pointsSebuah benda berbentuk balok dicelupkan dalam cairan A yang massa jenisnya 900 kg/m³, ternyata 1/3 bagian muncul di atas permukaan. Berapa bagian dari balok tersebut yang muncul jika cairan diganti dengan cairan B yang massa jenisnya 1200 kg/m³?
Benar
Kondisi 1: Benda dicelupkan dalam cairan A
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: W = 0\)
\(\text{F}_{\text{A}} = W\)
\(\rho_{A} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{A} \cdot g \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot g\)
\(900 \cdot \cancel{g} \cdot \dfrac{2}{3} \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(900 \cdot \dfrac{2}{3} = \rho_{\text{benda}}\)
\(\rho_{\text{benda}} = 600 \) kg/m³
Kondisi 2: Benda dicelupkan dalam cairan B
\(\text{F}_{\text{B}} = W\)
\(\rho_{B} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{B} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(1200 \cdot V_{t} = 600 V\)
\(V_{t} = \dfrac{600}{1200} V\)
\(V_{t} = \dfrac{1}{2} V\)
Bagian balok yang tercelup adalah ½ bagian, sehingga bagian balok yang muncul = ½ bagian
Salah
Kondisi 1: Benda dicelupkan dalam cairan A
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: W = 0\)
\(\text{F}_{\text{A}} = W\)
\(\rho_{A} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{A} \cdot g \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot g\)
\(900 \cdot \cancel{g} \cdot \dfrac{2}{3} \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(900 \cdot \dfrac{2}{3} = \rho_{\text{benda}}\)
\(\rho_{\text{benda}} = 600 \) kg/m³
Kondisi 2: Benda dicelupkan dalam cairan B
\(\text{F}_{\text{B}} = W\)
\(\rho_{B} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{B} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(1200 \cdot V_{t} = 600 V\)
\(V_{t} = \dfrac{600}{1200} V\)
\(V_{t} = \dfrac{1}{2} V\)
Bagian balok yang tercelup adalah ½ bagian, sehingga bagian balok yang muncul = ½ bagian
-
Pertanyaan 3 dari 14
3. Pertanyaan
1 pointsDua kubus yang identik dimasukkan dalam dua zat cair (B dan C) yang massa jenisnya berbeda. Bagian kubus yang masuk ke dalam zat cair B 50% dan zat cair C 30%. Perbandingan massa jenis zat B dan C adalah…
Benar
Kubus pertama dimasukkan ke dalam zat cair B
\(\text{F}_{\text{B}} = W\)
\(\rho_{B} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{B} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{B} \cdot \cancel{g} \cdot 50\% \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(\dfrac{1}{2} \cdot \rho_{B}= \rho_{\text{benda}}\)
\(\rho_{B}= 2\cdot \rho_{\text{benda}}\)
Kubus kedua dimasukkan ke dalam zat cair C
\(\text{F}_{\text{C}} = W\)
\(\rho_{C} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{C} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{C} \cdot \cancel{g} \cdot 30\% \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(\dfrac{3}{10} \cdot \rho_{C}= \rho_{\text{benda}}\)
\(\rho_{C}= \dfrac{10}{3} \cdot \rho_{\text{benda}}\)
\(\rho_{B} : \rho_{C} = 2\cdot \cancel{\rho_{\text{benda}}} : \dfrac{10}{3} \cdot \cancel{\rho_{\text{benda}}}\)
\(\rho_{B} : \rho_{C} = 2 : \dfrac{10}{3}\)
\(\rho_{B} : \rho_{C} = 6 : 10\)
\(\rho_{B} : \rho_{C} = 3 : 5\)
Salah
Kubus pertama dimasukkan ke dalam zat cair B
\(\text{F}_{\text{B}} = W\)
\(\rho_{B} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{B} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{B} \cdot \cancel{g} \cdot 50\% \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(\dfrac{1}{2} \cdot \rho_{B}= \rho_{\text{benda}}\)
\(\rho_{B}= 2\cdot \rho_{\text{benda}}\)
Kubus kedua dimasukkan ke dalam zat cair C
\(\text{F}_{\text{C}} = W\)
\(\rho_{C} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{C} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{C} \cdot \cancel{g} \cdot 30\% \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V} \cdot \cancel{g}\)
\(\dfrac{3}{10} \cdot \rho_{C}= \rho_{\text{benda}}\)
\(\rho_{C}= \dfrac{10}{3} \cdot \rho_{\text{benda}}\)
\(\rho_{B} : \rho_{C} = 2\cdot \cancel{\rho_{\text{benda}}} : \dfrac{10}{3} \cdot \cancel{\rho_{\text{benda}}}\)
\(\rho_{B} : \rho_{C} = 2 : \dfrac{10}{3}\)
\(\rho_{B} : \rho_{C} = 6 : 10\)
\(\rho_{B} : \rho_{C} = 3 : 5\)
-
Pertanyaan 4 dari 14
4. Pertanyaan
1 pointsBalok yang tingginya 40 cm dan massa jenisnya 0,75 gram/cm³ mengapung di atas zat cair yang massa jenisnya 1,5 gram/cm³, maka tinggi balok yang muncul di permukaan zat cair adalah…
Benar
\(\text{F}_{\text{A}} = W\)
\(\rho_{zat cair} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{zat cair} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{balok}} \cdot V \cdot \cancel{g}\)
\(1,5 \cdot \cancel{g} \cdot V_{t} = 0,75\cdot V \cdot \cancel{g}\)
\(1,5 \cdot V_{t} = 0,75 \cdot V\)
\(V_{t} = \dfrac{0,75}{1,5} V\)
\(V_{t} = \dfrac{1}{2} V\)
\(\text{Luas alas × tinggi tercelup} = \dfrac{1}{2} \cdot \text{Luas alas × tinggi balok}\)
\(\text{Tinggi tercelup} = \dfrac{1}{2} \text{tinggi balok}\)
\(\text{Tinggi tercelup} = \dfrac{1}{2} \cdot 40 \text{ cm}\)
\(\text{Tinggi tercelup} = 20 \text{ cm}\)
Tinggi balok yang muncul di permukaan zat cair = 40 − 20 = 20 cm
Salah
\(\text{F}_{\text{A}} = W\)
\(\rho_{zat cair} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{zat cair} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{balok}} \cdot V \cdot \cancel{g}\)
\(1,5 \cdot \cancel{g} \cdot V_{t} = 0,75\cdot V \cdot \cancel{g}\)
\(1,5 \cdot V_{t} = 0,75 \cdot V\)
\(V_{t} = \dfrac{0,75}{1,5} V\)
\(V_{t} = \dfrac{1}{2} V\)
\(\text{Luas alas × tinggi tercelup} = \dfrac{1}{2} \cdot \text{Luas alas × tinggi balok}\)
\(\text{Tinggi tercelup} = \dfrac{1}{2} \text{tinggi balok}\)
\(\text{Tinggi tercelup} = \dfrac{1}{2} \cdot 40 \text{ cm}\)
\(\text{Tinggi tercelup} = 20 \text{ cm}\)
Tinggi balok yang muncul di permukaan zat cair = 40 − 20 = 20 cm
-
Pertanyaan 5 dari 14
5. Pertanyaan
1 pointsPada saat benda dicelupkan ke dalam cairan X, 0,8 bagian benda berada di atas permukaan cairan, sedangkan pada saat benda dicelupkan ke dalam cairan Y, 0,5 bagian bagian benda berada di atas permukaan cairan. Jika massa jenis cairan X adalah 2000 kg/m³, maka massa jenis cairan Y adalah…
Benar
Kondisi 1: Benda dicelupkan ke dalam cairan X
\(\text{F}_{\text{A}} = W\)
\(\rho_{x} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{x} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(2000 \cdot (1\:-\:0,8) \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V}\)
\(2000 \cdot (0,2) = \rho_{\text{benda}}\)
\(\rho_{\text{benda}} = 400\) kg/m³
Kondisi 2: Benda dicelupkan ke dalam cairan Y
\(\text{F}_{\text{A}} = W\)
\(\rho_{y} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{y} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{y} \cdot (1\:-\:0,5) \cancel{V} = 400 \cdot \cancel{V}\)
\(\rho_{y} \cdot (0,5)= 400 \)
\(\rho_{y} = 400 \times \dfrac{2}{1} \)
\(\rho_{y} = 800 \) kg/m³
Jadi, massa jenis cairan Y adalah 800 kg/m³
Salah
Kondisi 1: Benda dicelupkan ke dalam cairan X
\(\text{F}_{\text{A}} = W\)
\(\rho_{x} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{x} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(2000 \cdot (1\:-\:0,8) \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V}\)
\(2000 \cdot (0,2) = \rho_{\text{benda}}\)
\(\rho_{\text{benda}} = 400\) kg/m³
Kondisi 2: Benda dicelupkan ke dalam cairan Y
\(\text{F}_{\text{A}} = W\)
\(\rho_{y} \cdot g \cdot V_{t} = m \cdot g\)
\(\rho_{y} \cdot \cancel{g} \cdot V_{t} = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(\rho_{y} \cdot (1\:-\:0,5) \cancel{V} = 400 \cdot \cancel{V}\)
\(\rho_{y} \cdot (0,5)= 400 \)
\(\rho_{y} = 400 \times \dfrac{2}{1} \)
\(\rho_{y} = 800 \) kg/m³
Jadi, massa jenis cairan Y adalah 800 kg/m³
-
Pertanyaan 6 dari 14
6. Pertanyaan
1 pointsBalok kayu terapung di atas permukaan dari dua cairan yang berbeda yaitu bensin (ρ = 700 kg/m³) dan air (ρ = 1.000 kg/m³). Seperti pada gambar, massa jenis balok adalah…
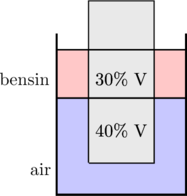 Benar
Benar
\(\text{F}_{\text{air}} + \text{F}_{\text{bensin}} =\text{W}\)
\(\rho_{\text{air}} \cdot \cancel{g} \cdot V_t + \rho_{\text{bensin}} \cdot \cancel{g} \cdot V_t = m \cdot \cancel{g}\)
\(1000 \cdot 40\% \cancel{V} + 700 \cdot 30\% \cancel{V} = \rho_{\text{balok}} \cdot \cancel{V}\)
\(1000 \cdot 0,40 + 700 \cdot 0,30 = \rho_{\text{balok}}\)
\(400 + 210 = \rho_{\text{balok}}\)
\(\rho_{\text{balok}} = 610\) kg/m³
Salah
\(\text{F}_{\text{air}} + \text{F}_{\text{bensin}} =\text{W}\)
\(\rho_{\text{air}} \cdot \cancel{g} \cdot V_t + \rho_{\text{bensin}} \cdot \cancel{g} \cdot V_t = m \cdot \cancel{g}\)
\(1000 \cdot 40\% \cancel{V} + 700 \cdot 30\% \cancel{V} = \rho_{\text{balok}} \cdot \cancel{V}\)
\(1000 \cdot 0,40 + 700 \cdot 0,30 = \rho_{\text{balok}}\)
\(400 + 210 = \rho_{\text{balok}}\)
\(\rho_{\text{balok}} = 610\) kg/m³
-
Pertanyaan 7 dari 14
7. Pertanyaan
1 pointsSebuah balok kayu bermassa 7,5 kg dan bervolume 0,01 m³ dimasukkan ke dalam air (ρ = 1000 kg/m³). Besar gaya untuk menahan balok agar terbenam seluruhnya di dalam air adalah…
Benar
Menghitung tegangan tali T yang menekan balok
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: \text{T} \:-\: \text{W} = 0\)
\(\text{F}_{\text{A}} = \text{T} + \text{W}\)
\(\rho_{\text{air}} \cdot g \cdot V = \text{T} + m \cdot g\)
\(1000 \cdot 10 \cdot 0,01 = \text{T} + 7,5 \cdot 10\)
\(100 = \text{T} + 75\)
\(\text{T} = 100 \:-\:75\)
\(\text{T} = 25 \text{ N}\)
Salah
Menghitung tegangan tali T yang menekan balok
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: \text{T} \:-\: \text{W} = 0\)
\(\text{F}_{\text{A}} = \text{T} + \text{W}\)
\(\rho_{\text{air}} \cdot g \cdot V = \text{T} + m \cdot g\)
\(1000 \cdot 10 \cdot 0,01 = \text{T} + 7,5 \cdot 10\)
\(100 = \text{T} + 75\)
\(\text{T} = 100 \:-\:75\)
\(\text{T} = 25 \text{ N}\)
-
Pertanyaan 8 dari 14
8. Pertanyaan
1 pointsSebuah balok kayu bermassa 7,5 kg dan bervolume V diikatkan ke dasar sebuah tanki yang berisi air (ρ = 1000 kg/m³) sehingga balok terbenam seluruhnya. Jika besar tegangan tali 25 N. Nilai V adalah…
Benar
Menghitung tegangan tali T yang menahan balok agar tidak terapung
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: \text{T} \:-\: \text{W} = 0\)
\(\text{F}_{\text{A}} = \text{T} + \text{W}\)
\(\rho_{\text{air}} \cdot g \cdot V = \text{T} + m \cdot g\)
\(1000 \cdot 10 \cdot V = \text{T} + 7,5 \cdot 10\)
\(1000 \cdot 10 \cdot V = 25 + 7,5 \cdot 10\)
\(10.000 \cdot V = 100\)
\(V = \dfrac{100}{10.000}\)
\(V = \dfrac{1}{100}\) m³
\(V = 0,01\) m³
Salah
Menghitung tegangan tali T yang menahan balok agar tidak terapung
\(\sum \text{F}_y = 0\)
\(\text{F}_{\text{A}} \:-\: \text{T} \:-\: \text{W} = 0\)
\(\text{F}_{\text{A}} = \text{T} + \text{W}\)
\(\rho_{\text{air}} \cdot g \cdot V = \text{T} + m \cdot g\)
\(1000 \cdot 10 \cdot V = \text{T} + 7,5 \cdot 10\)
\(1000 \cdot 10 \cdot V = 25 + 7,5 \cdot 10\)
\(10.000 \cdot V = 100\)
\(V = \dfrac{100}{10.000}\)
\(V = \dfrac{1}{100}\) m³
\(V = 0,01\) m³
-
Pertanyaan 9 dari 14
9. Pertanyaan
1 pointsSebuah balok plastik homogen mengapung di suatu bejana air. Seperlima bagian balok berada di atas permukaan air. Jika volume balok V dan massa air sebanyak V tersebut adalah 12 g, maka massa balok adalah… gram
Benar
Langkah 1: Menghitung volume balok plastik
Diketahui volume balok V dan massa air sebanyak V tersebut adalah 12 g.
\(\rho_{\text{air}} = \dfrac{m}{V}\)
\(1000 = \dfrac{12 \times 10^{-3}}{V}\)
\(V = \dfrac{12 \times 10^{-3}}{1000}\)
\(V = 1,2 \times 10^{-5}\) m³
Volume balok plastik adalah \(1,2 \times 10^{-5}\) m³
Langkah 2: menghitung massa balok plastik
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot g \cdot V_{t} = m \cdot g\)
\(1000\cdot \cancel{g} \cdot (1\:-\: \frac{1}{5}) V = m \cdot \cancel{g}\)
\(1000\cdot \frac{4}{5})\times 1,2 \times 10^{-5} = m\)
\(m = 9,6 \times 10^{-3}\) kg
\(m = 9,6\) g
Jadi, massa balok tersebut adalah 9,6 gram
Salah
Langkah 1: Menghitung volume balok plastik
Diketahui volume balok V dan massa air sebanyak V tersebut adalah 12 g.
\(\rho_{\text{air}} = \dfrac{m}{V}\)
\(1000 = \dfrac{12 \times 10^{-3}}{V}\)
\(V = \dfrac{12 \times 10^{-3}}{1000}\)
\(V = 1,2 \times 10^{-5}\) m³
Volume balok plastik adalah \(1,2 \times 10^{-5}\) m³
Langkah 2: menghitung massa balok plastik
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot g \cdot V_{t} = m \cdot g\)
\(1000\cdot \cancel{g} \cdot (1\:-\: \frac{1}{5}) V = m \cdot \cancel{g}\)
\(1000\cdot \frac{4}{5})\times 1,2 \times 10^{-5} = m\)
\(m = 9,6 \times 10^{-3}\) kg
\(m = 9,6\) g
Jadi, massa balok tersebut adalah 9,6 gram
-
Pertanyaan 10 dari 14
10. Pertanyaan
1 pointsGaya Archimedes yang bekerja pada benda saat dimasukkan ke dalam fluida ditentukan oleh…
Benar
Salah
-
Pertanyaan 11 dari 14
11. Pertanyaan
1 pointsSepotong kaca di udara memiliki berat 25 N. Jika dimasukkan ke dalam air beratnya menjadi 15 N. Bila massa jenis air adalah 1000 kg/m³ dan percepatan gravitasinya 10 m/s², maka massa jenis kaca adalah…
Benar
Langkah 1: Menghitung gaya Archimedes
Gaya Archimedes = Berat kaca di udara − Berat kaca di dalam air
\(\text{F}_{\text{A}} = 25 \:-\:15 \text{ N}\)
\(\text{F}_{\text{A}} = 10 \text{ N}\)
Langkah 2: Menghitung volume kaca
\(\text{F}_{\text{A}} = \rho_{\text{air}} \cdot g \cdot V_t\)
\(10 = 1000\cdot 10 \cdot V\)
\(V = \dfrac{10}{10.000}\)
\(V = 1 \times 10^{-3}\) m³
Langkah 3: Menghitung massa jenis kaca
Karena berat kaca di udara adalah 25 N, maka massa kaca adalah 2,5 kg
note: gunakan rumus W = m.g
\(\rho = \dfrac{m}{V}\)
\(\rho = \dfrac{2,5}{1 \times 10^{-3}}\)
\(\rho = 2,5 \times 10^3 \) kg/m³
jadi, massa jenis kaca adalah \(2,5 \times 10^3 \) kg/m³
Salah
Langkah 1: Menghitung gaya Archimedes
Gaya Archimedes = Berat kaca di udara − Berat kaca di dalam air
\(\text{F}_{\text{A}} = 25 \:-\:15 \text{ N}\)
\(\text{F}_{\text{A}} = 10 \text{ N}\)
Langkah 2: Menghitung volume kaca
\(\text{F}_{\text{A}} = \rho_{\text{air}} \cdot g \cdot V_t\)
\(10 = 1000\cdot 10 \cdot V\)
\(V = \dfrac{10}{10.000}\)
\(V = 1 \times 10^{-3}\) m³
Langkah 3: Menghitung massa jenis kaca
Karena berat kaca di udara adalah 25 N, maka massa kaca adalah 2,5 kg
note: gunakan rumus W = m.g
\(\rho = \dfrac{m}{V}\)
\(\rho = \dfrac{2,5}{1 \times 10^{-3}}\)
\(\rho = 2,5 \times 10^3 \) kg/m³
jadi, massa jenis kaca adalah \(2,5 \times 10^3 \) kg/m³
-
Pertanyaan 12 dari 14
12. Pertanyaan
1 pointsSebuah gabus dimasukkan dalam air ternyata 75% volume gabus tercelup dalam air, maka massa jenis gabus adalah…
Benar
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot \cancel{g}\cdot V_t = \rho_{\text{gabus}} \cdot V \cdot \cancel{g}\)
\(1000 \cdot 75\% \cancel{V} = \rho_{\text{gabus}} \cdot \cancel{V}\)
\(1000 \cdot 0,75 = \rho_{\text{gabus}}\)
\(750 = \rho_{\text{gabus}}\)
Jadi, massa jenis gabus tersebut adalah 750 kg/m³ = 0,75 g/cm³
Salah
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot \cancel{g}\cdot V_t = \rho_{\text{gabus}} \cdot V \cdot \cancel{g}\)
\(1000 \cdot 75\% \cancel{V} = \rho_{\text{gabus}} \cdot \cancel{V}\)
\(1000 \cdot 0,75 = \rho_{\text{gabus}}\)
\(750 = \rho_{\text{gabus}}\)
Jadi, massa jenis gabus tersebut adalah 750 kg/m³ = 0,75 g/cm³
-
Pertanyaan 13 dari 14
13. Pertanyaan
1 pointsSebuah ban mobil berisi udara digunakan sebagai pengapung di dalam air, volume ban 0,1 m³ dan massanya 1 kg. Jika massa jenis air 1 gr/cm³ dan percepatan gravitasi g = 10 m/s², maka ban dapat menahan dan mengapungkan beban maksimum sebesar…
Benar
\(\text{F}_{\text{A}} = W_{\text{ban}} + W_{\text{beban}}\)
\(\rho_{\text{air}} \cdot g \cdot Vt = W_{\text{ban}} + W_{\text{beban}}\)
\(1000 \cdot 10 \cdot 0,1 = 1 \cdot 10 + W_{\text{beban}}\)
\(1000 = 10 + W_{\text{beban}}\)
\(990 = m \cdot g\)
\(990 = m \cdot 10\)
\(m = 99 \text{ kg}\)
Jadi, massa beban maksimum = 99 kg
Salah
\(\text{F}_{\text{A}} = W_{\text{ban}} + W_{\text{beban}}\)
\(\rho_{\text{air}} \cdot g \cdot Vt = W_{\text{ban}} + W_{\text{beban}}\)
\(1000 \cdot 10 \cdot 0,1 = 1 \cdot 10 + W_{\text{beban}}\)
\(1000 = 10 + W_{\text{beban}}\)
\(990 = m \cdot g\)
\(990 = m \cdot 10\)
\(m = 99 \text{ kg}\)
Jadi, massa beban maksimum = 99 kg
-
Pertanyaan 14 dari 14
14. Pertanyaan
1 pointsSebuah benda mengapung di atas air dengan massa jenis air 1 gram/cm³. Jika 7/10 bagian dari benda berada di bawah permukaan air, maka massa jenis benda adalah…
Benar
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot g \cdot V_t = m \cdot g\)
\(\rho_{\text{air}} \cdot \cancel{g} \cdot V_t = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(1 \cdot \dfrac{7}{10} \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V}\)
\(0,7 = \rho_{\text{benda}}\)
Jadi, massa jenis benda tersebut adalah 0,7 gram/cm³
Salah
\(\text{F}_{\text{A}} = W\)
\(\rho_{\text{air}} \cdot g \cdot V_t = m \cdot g\)
\(\rho_{\text{air}} \cdot \cancel{g} \cdot V_t = \rho_{\text{benda}} \cdot V \cdot \cancel{g}\)
\(1 \cdot \dfrac{7}{10} \cancel{V} = \rho_{\text{benda}} \cdot \cancel{V}\)
\(0,7 = \rho_{\text{benda}}\)
Jadi, massa jenis benda tersebut adalah 0,7 gram/cm³
