Interferensi gelombang adalah perpaduan dua gelombang yang koheren. Dua gelombang disebut koheren apabila kedua gelombang tersebut memiliki frekuensi dan amplitudo yang sama serta memiliki selisih fase yang tetap/konstan.
Percobaan interferensi cahaya pada celah ganda dilakukan oleh Thomas Young.
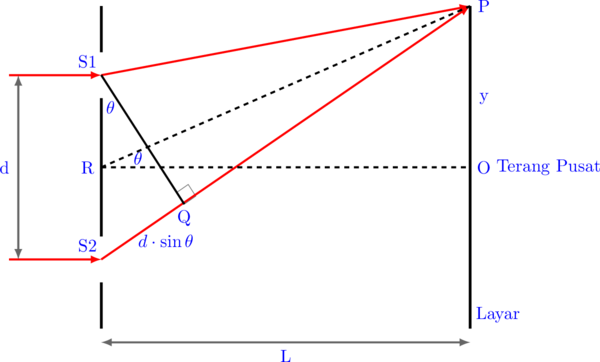
Interferensi konstruktif (saling menguatkan/pola terang)
di P terjadi interferensi maksimum jika:
\(\text{S}_2 \text{P}\:-\:\text{S}_1\text{P} = d \cdot \sin \theta = n \cdot \lambda\)
$$\bbox[yellow, 5px, border: 2px solid red] {d\cdot \sin \theta = n \cdot \lambda}$$
Keterangan:
\(\theta\) = sudut simpangan antara sinar dan layar
\(\lambda\) = panjang gelombang
\(d\) = jarak antar celah
\(n = 0, \pm1, \pm2, \pm3, \dotso\) (orde atau terang ke-n)
Rumus di atas juga dapat ditulis sebagai berikut:
$$\bbox[yellow, 5px, border: 2px solid red] {d \cdot \dfrac{y}{L} = n \cdot \lambda}$$
Keterangan:
\(\sin \theta \thickapprox \tan \theta\)
\(d\) = jarak antar celah
\(y\) = jarak antara garis terang ke terang pusat
\(L\) = jarak celah ke layar
\(\lambda\) = panjang gelombang
\(n = 0, \pm1, \pm2, \pm3, \dotso\) (orde atau terang ke-n)
Konversi satuan panjang angstrom ke meter:
\(1 \text{ A}^{\circ} = 1 \times 10^{-10}\text{ meter}\)
Interferensi destruktif (saling melemahkan/pola gelap)
$$\bbox[yellow, 5px, border: 2px solid red] {d\cdot \sin \theta = (n\:-\:\dfrac{1}{2})\cdot \lambda}$$
Keterangan:
\(\theta\) = sudut simpangan antara sinar dan layar
\(\lambda\) = panjang gelombang
\(d\) = jarak antar celah
\(n = \pm1, \pm2, \pm3, \dotso\) (orde atau gelap ke-n)
Rumus di atas juga dapat ditulis sebagai berikut:
$$\bbox[yellow, 5px, border: 2px solid red] {d \cdot \dfrac{y}{L} = (n\:-\:\dfrac{1}{2}) \cdot \lambda}$$
Keterangan:
\(d\) = jarak antar celah
\(y\) = jarak antara garis gelap ke terang pusat
\(L\) = jarak celah ke layar
\(\lambda\) = panjang gelombang
\(n = \pm1, \pm2, \pm3, \dotso\) (orde atau gelap ke-n)
Jarak antara pita terang dan pita gelap yang berdekatan
$$\bbox[yellow, 5px, border: 2px solid red] {\triangle y = \dfrac{L \cdot \lambda}{2d}}$$
Jarak antara dua garis terang yang berdekatan atau dua garis gelap yang berdekatan adalah \(2\triangle y\)
LATIHAN SOAL
Soal 01
Percobaan Young digunakan dua celah sempit berjarak 2 mm satu sama lain dan layar yang dipasang 1 m dari celah tersebut. Jika dihasilkan terang kedua pada jarak 0,5 mm dari terang pusat, maka panjang gelombang cahaya yang digunakan adalah…
(A) \(5 \times 10^{-7} \text{ meter}\)
(B) \(5 \times 10^{-8} \text{ meter}\)
(C) \(6 \times 10^{-9} \text{ meter}\)
(D) \(6 \times 10^{-10} \text{ meter}\)
(E) \(8 \times 10^{-10} \text{ meter}\)
Soal 02
Sebuah celah ganda disinari dengan cahaya yang panjang gelombangnya 600 nm. Sebuah layar diletakkan 2 m dari celah. Jika jarak kedua celah 0,24 mm maka jarak pita terang keempat dengan terang pusat adalah…
(A) 2,0 cm
(B) 6,0 cm
(C) 8,0 cm
(D) 12 cm
(E) 20 cm
Soal 03
Seberkas cahaya monokromatik dijatuhkan pada dua celah sempit, sehingga terjadi interferensi yang dapat terlihat di layar. Dari pernyataan berikut :
(1) Semakin dekat jarak layar ke celah semakin jauh jarak antar pita
(2) Semakin dekat jarak layar ke celah semakin dekat jarak antar pita
(3) Semakin jauh dari terang pusat intensitas semakin kecil
(4) Semakin jauh dari terang pusat intensitas semakin besar
Pernyataan yang benar adalah…
(A) (3) dan (4)
(B) (2) dan (4)
(C) (2) dan (3)
(D) (1) dan (4)
(E) (1) dan (3)
Soal 04
Cahaya dari suatu sumber melalui dua celah sempit yang terpisah sejauh 0,1 mm. Jika jarak celah dengan layar 100 cm dan jarak antara garis gelap pertama dan garis terang pertama adalah 2,95 mm, maka panjang gelombang cahaya yang digunakan adalah…
(A) 2100 nm
(B) 1080 nm
(C) 590 nm
(D) 480 nm
(E) 440 nm